Решение. Часть 1.

ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ

Напомним основные сведения из гладкого конечномерного анализа. Пусть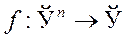

функция n вещественных переменных, гладкая в некоторой открытой области 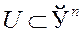(в данном случае гладкость функции означает, что у нее имеются частные производные всех порядков в каждой точке области U). Пусть 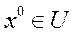точка локального минимума функции 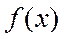, то есть найдется такое 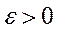, что для всех , . Здесь обозначает евклидово расстояние между точками пространства 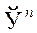, 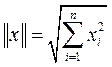. Теорема Ферма утверждает, что в точке локального минимума выполнено n соотношений типа равенства

, , …, .

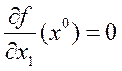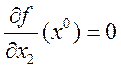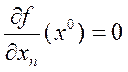ЗАДАЧА 1. Найти локальный минимум функции

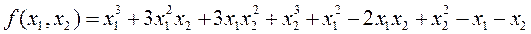
Решение. Часть 1.

Воспользуемся теоремой Ферма и выпишем необходимые условия локального минимума.

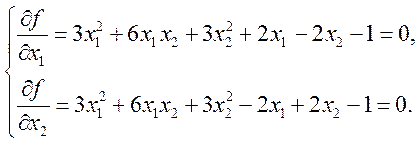
Вычитая из первого уравнения второе, получим

откуда

, .

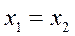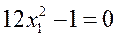Следовательно, у нас имеет две точки, координаты которых удовлетворяют условиям теоремы Ферма:

, .

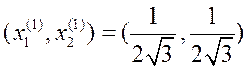Теорема Ферма дает лишь необходимые, но отнюдь не достаточные условия минимума. На самом деле из этих двух точек только одна является точкой минимума.

Обозначим матрицу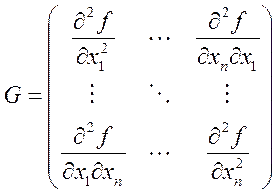

Матрица G называется гессианом функции .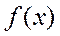

Критерий Сильвестра.

Рассмотрим главные окаймляющие миноры матрицы A,

,

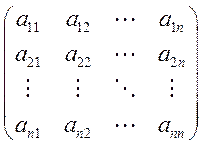то есть n определителей последовательно вложенных друг в друга матриц

, , , …, .

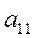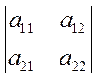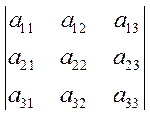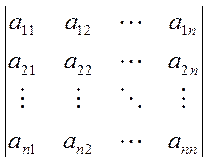Тогда, если все числа в этой цепочке положительны, то матрица A положительно определена, если имеет место знакочередование, начиная со знака минус, то матрица A отрицательно определена. Если ни первое, ни второе условия не выполнены, то матрица A является знаконеопределенной.

1 случай. 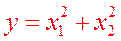. Эллиптический параболоид.

O

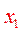
Поскольку , значение 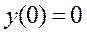является и локальным, и абсолютным минимумом, поэтому начало координат является точкой локального минимума.

2 случай. . Перевернутый эллиптический параболоид.

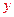
O

В данном случае имеем 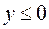, поэтому 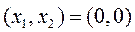является точкой локального максимума.

3 случай. 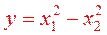. Гиперболический параболоид (седло).

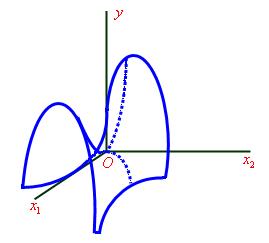
Начало координат 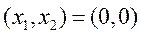не является ни локальным минимумом, ни локальным максимумом. Сколь угодно близко от точки на сечении параболоида плоскостью функция принимает положительные значения. Поэтому не является локальным максимумом. С другой стороны, на сечении гиперболоида плоскостью функция принимает отрицательные значения, поэтому значение не является локальным минимумом. Очень похожая структура имеется у графика функции

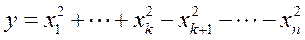при произвольных n.

Теперь мы можем вернуться к решению Задачи 1 и определить характер экстремума у критических точек функции