Решение ЗАДАЧИ 1. Часть 2.

Напомним, что

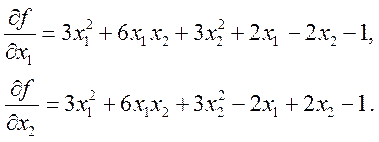
Дифференцируя частные производные еще раз, получим

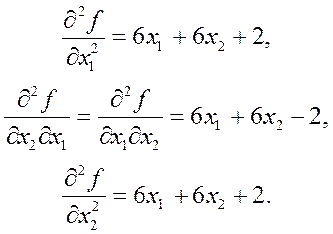
Гессиан функции представляется матрицей

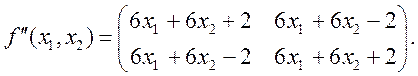
Рассмотрим первую точку экстремума 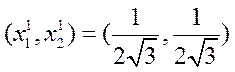. Для нее

Используем критерий Сильвестра.

, .

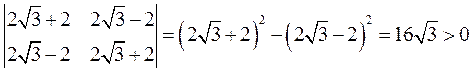Следовательно, гессиан является положительно определенной матрицей, и точка 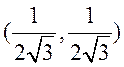является точкой локального минимума.

Теперь рассмотрим точку 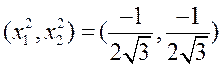. Для нее получаем

Критерий Сильвестра дает

, .

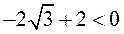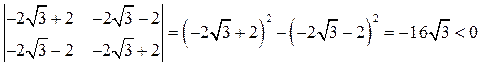Следовательно, точка не является ни точкой минимума, ни точкой максимума.

Задача 2.

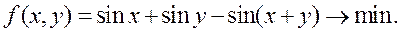
Решение.

Имеем:

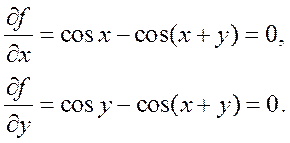
Из первого уравнения получаем

либо .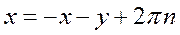

Из второго уравнения получаем

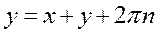либо .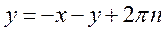

В результате получаем либо 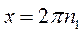, , 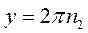либо . В первом случае 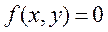, во втором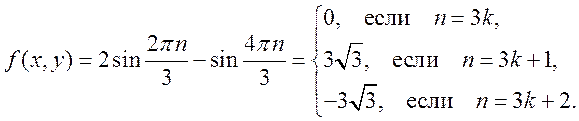

ОТВЕТ. 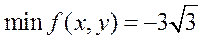и достигается при .

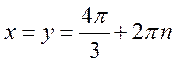Задача 3. Найти минимум функции

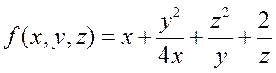
в области , , .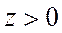