
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные случайные величины
|
|
Определение 9.9. Непрерывной случайной величиной (кратко: н.с.в.) называется с.в.X, если множество ее возможных значений непрерывно заполняют конечный или бесконечный промежуток на числовой оси.
Более строгое определение н.с.в. можно дать, используя понятие функции распределения.
Определение 9.9(а). Случайная величина X называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси.
В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю: Р{Х=с}=0, 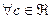 . Поэтому для н. с. в. X имеем:
. Поэтому для н. с. в. X имеем:
Р{а  Х< b} = Р{а< Х< b} = Р{а< Х
Х< b} = Р{а< Х< b} = Р{а< Х  b} = Р{а
b} = Р{а  Х
Х  b} = F(b) – F(а).
b} = F(b) – F(а).
Помимо функции распределения для непрерывных случайных величин, существует еще один удобный способ задания закона распределения – плотность вероятности.
Определение 9.10. Пусть функция распределения F(x) данной н.с.в. X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек. Тогда производная f(x) ее функции распределения называется плотностью распределения непрерывной с.в.X (или плотностью вероятности): f(x)=F'(x). График плотности распределения f(x) называется кривой распределения.
Плотность распределения обладает следующими свойствами:
1. f(x) 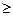 0 (свойство неотрицательности);
0 (свойство неотрицательности);
2. 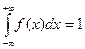 (свойство нормированности);
(свойство нормированности);
3. Р{а  Х
Х  b}=
b}= 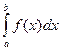 ;
;
4. F(x)= 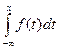 ;
;
5. 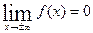 .
.
Пример 9.4. Задана функция распределения н.с.в. X:
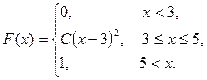 Найдите: а) коэффициент С;
Найдите: а) коэффициент С;
б) плотность распределения f(x) и постройте графики функций F(x) и f(x);
в) Р{3  Х< 4}.
Х< 4}.
Решение. а) Так как с.в. Х непрерывна, то F(x) должна быть непрерывной функцией в любой точке, в частности, и при х=5. Так как F(5)=1, то 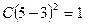 , откуда С=
, откуда С= 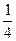 .
.
б) Для нахождения f(x) воспользуемся определением f(x)=F'(x).
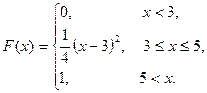 | 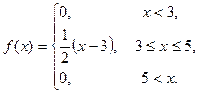 |
 Графики функции распределения и плотности распределения см. на рис.9.4 и 9.5 соответственно.
Графики функции распределения и плотности распределения см. на рис.9.4 и 9.5 соответственно.
Рис.9.4 Рис.9.5
в) Р{3  Х< 4}=Р{3
Х< 4}=Р{3  Х
Х  4}=
4}= 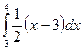 =
= 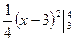 =
= 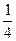 .
.
Пример 9.5. При каком значении параметра С функция f(x):
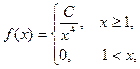 может быть плотностью распределения некоторой непрерывной с.в. X? Найдите функцию распределения вероятностей F(x) и постройте графики f(x) и F(x).
может быть плотностью распределения некоторой непрерывной с.в. X? Найдите функцию распределения вероятностей F(x) и постройте графики f(x) и F(x).
Решение. Очевидно, что f(x)> 0 при C> 0, 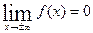 . Используя свойство нормированности
. Используя свойство нормированности 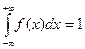 , найдем значение параметра С.
, найдем значение параметра С.
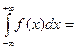
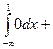

 =
= 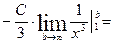
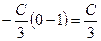 .
.
Отсюда получим, что С=3.
 Т.о. Для нахождения функции распределения вероятностей используем формулу F(x)=
Т.о. Для нахождения функции распределения вероятностей используем формулу F(x)= 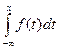 .
.
При x< 1 имеем: F(x)= 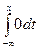 =0.
=0.
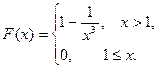 При x
При x 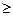 1 имеем F(x)=
1 имеем F(x)= 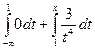 =
=  .
.
Т.о.
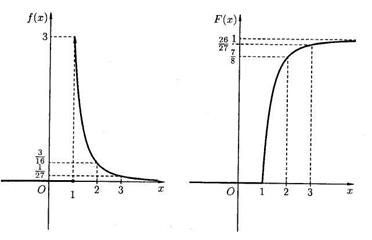 Графики функции распределения и плотности распределения см. на рис.9.6 и 9.7 соответственно.
Графики функции распределения и плотности распределения см. на рис.9.6 и 9.7 соответственно.
Рис.9.6 Рис.9.7
Решите задачи:
1. Какая из нижеприведенных последовательностей является распределением вероятностей некоторой дискретной случайной величины (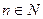 ): а)
): а)  ; б)
; б) 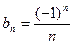 ; в)
; в) 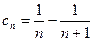 ; г)
; г) 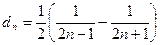 .
.
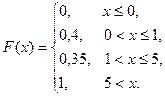 2. Может ли функция F(x) быть функцией распределения некоторой случайной величины, если: а)
2. Может ли функция F(x) быть функцией распределения некоторой случайной величины, если: а) 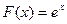 ;
;
б) 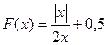 ; в)
; в) 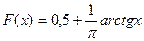 ; г)
; г)
3. Даны значения, принимаемые д.с.в. X: 10, 2, 8, 4; и соответствующие им вероятности: 0, 3, 0, 4, 0, 1, 0, 2. Постройте ряд и полигон распределения д.с.в. X. Найдите функцию распределения F(x) д.с.в. X и постройте ее график.
| xi | –3 | –1 | ||
| pi | 0, 1 | 0, 2 | 0, 4 | р |
4. Дискретная с.в.Х задана рядом распределения:
а) Найдите значение р.
б) Найдите функцию распределения F(x) д.с.в.X.
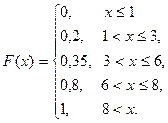 в) Постройте ряды распределения с.в. Z=3Х и W=Х2.
в) Постройте ряды распределения с.в. Z=3Х и W=Х2.
5. Задана функция распределения F(x) д.с.в. X:
Постройте ряд распределения д.с.в. X.
Найдите вероятности: Р{Х=1}, Р{2< X  4}.
4}.
6. Построить ряд и полигон распределения д.с.в. X числа попаданий мяча в ворота при двух одиннадцатиметровых ударах, если вероятность попадания при одном ударе равна 0, 7. Найдите функцию распределения F(x) д.с.в. X и постройте ее график.
7. Монета подбрасывается 3 раза. Постройте ряд и полигон распределения д.с.в. X числа выпадений герба. Найдите функцию распределения F(x) д.с.в. X и постройте ее график. Найдите P{X< 2}, Р{0  Х< 2}, Р{0< X
Х< 2}, Р{0< X  2}, P{X> 2}.
2}, P{X> 2}.
8. В урне имеется четыре шара с номерами от 1 до 4. Вынули два шара. Постройте ряд и полигон распределения с.в. X суммы номеров вытащенных шаров. Найдите функцию распределения F(x) д.с.в. X и постройте ее график.
9. Абитуриент должен сдать три экзамена. Вероятность успешной сдачи 1-го экзамена равна 0, 5, 2-го – 0, 6, 3-го – 0, 8. Постройте ряд и полигон распределения с.в. X числа экзаменов, сданных абитуриентом. Найдите функцию распределения F(x) д.с.в. X и постройте ее график.
10. В команде 16 спортсменов, из которых 6 перворазрядников. Наудачу выбирают двух спортсменов. Постройте ряд и полигон распределения д.с.в. X числа перворазрядников среди выбранных спортсменов. Найдите функцию распределения F(x) д.с.в. X и постройте ее график.
11. Даны законы распределения двух независимых дискретных случайных величин Х и Y:
| xi | –3 | –2 | –1 |
| pi | 0, 5 | 0, 4 | 0, 1 |
| yi | ||
| pi | 0, 3 | 0, 7 |
Найдите законы распределения с.в.: а) Z=Х+Y; б) V=X–Y; в) W=X∙ Y.
12. Может ли при каком-либо значении аргумента быть:
а) Функция распределения – больше единицы?
б) Плотность распределения – больше единицы?
в) Функция распределения – отрицательной?
 г) Плотность распределения – отрицательной?
г) Плотность распределения – отрицательной?
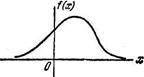
13. Дан график плотности распределения f(x) случайной величины X (рис.9.8). Как изменится этот график, если:
а) прибавить к случайной величине 1; Рис.9.8
б) вычесть из случайной величины 2;
в) умножить случайную величину на 2;
г) изменить знак величины на противоположный?
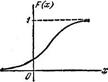 14. Дан график функции распределения F(x) случайной величины X (рис.9.9). Как изменится этот график, если:
14. Дан график функции распределения F(x) случайной величины X (рис.9.9). Как изменится этот график, если:
а) прибавить к случайной величине 1;
б) вычесть из случайной величины 2; Рис.9.9
в) умножить случайную величину на 2;
г) изменить знак случайной величины на противоположный?
15. Н.с.в. Х подчинена закону распределения с плотностью f(x):
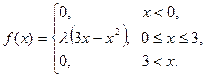 а) Найдите коэффициент
а) Найдите коэффициент  .
.
б) Постройте график f(x).
в) Найдите Р{1< Х< 2}.
16. Н.с.в. Х подчинена закону распределения с плотностью f(x):
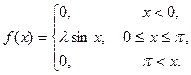 а) Найдите коэффициент
а) Найдите коэффициент  .
.
б) Найдите F(x).
в) Постройте графики f(x) и F(x).
17. Н.с.в. Х задана функцией распределения F(x):
 а) Найдите плотность вероятности f(x);
а) Найдите плотность вероятности f(x);
б) Постройте графики f(x) и F(x).
в) Найдите Р{0< Х< 2} и Р{2< Х< 5}.
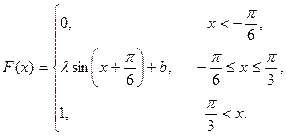 18. Н.с.в. Х задана функцией распределения F(x):
18. Н.с.в. Х задана функцией распределения F(x):
а) Найдите коэффициенты  и b.
и b.
б) Найдите плотность f(x).
в) Найдите Р{0  Х<
Х< 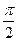 }.
}.
19. Н.с.в. Х задана функцией распределения F(x):
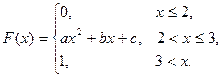 Парабола
Парабола 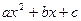 имеет вершину в точке с абсциссой x=2.
имеет вершину в точке с абсциссой x=2.
а) Найдите коэффициенты a, b и c.
б) Найдите плотность f(x).
в) Постройте графики f(x) и F(x).
г) Найдите P{X> 5}, Р{2  Х< 5}, Р{0
Х< 5}, Р{0  Х< 2, 5}.
Х< 2, 5}.
 20. Задан график функции распределения F(x) н.с.в.X (см. рис.9.10). Найдите аналитическое выражение для f(x) и F(x).
20. Задан график функции распределения F(x) н.с.в.X (см. рис.9.10). Найдите аналитическое выражение для f(x) и F(x).
Рис.9.10