
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретная случайная величина
|
|
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Законом распределения дискретной случайной величины называют соответствие между всеми возможными значениями x1., x2, x3, … случайной величины X и их вероятностями p1, p2, p3, … (pi=P(X=xi)), причем p1+p2+p3+…=1. Закон распределения задается таблично, аналитически или графически. При табличном задании закона распределения первая строка таблицы содержит возможные значения случайной величины X, а вторая - их вероятности:
| X | x1 | x2 
| x3 | … |
| p | p1 | p2 | p3 | … |
Для наглядности закона распределения дискретной случайной величины изображают графически, длячего в прямоугольной системе координат строят точки (xi, pi)исоединяют их последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины X.
2.1 Задача. В урне 7 шаров, из которых 4 белых, а остальные черные. Из урны наудачу извлекаются 3 шара; Х - число извлеченных белых шаров. Найдите закон распределения дискретной случайной величины ипостройте многоугольник и функцию распределения.
Решение. Возможные значения случайной величины Х: 0, 1, 2, 3. Соответствующие им вероятностиp0, p1, p2, p3 подсчитываем классическим способом:
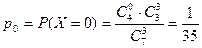 ;
; 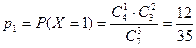
 ;
; 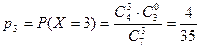
Закон распределения X
| X | ||||
| p | 1/35 | 12/35 | 18/35 | 4/35 |
Проверка: 1/35+12/35+18/35+4/35=1. Многоугольник распределения изображен на рисунке 1.
Найдем функцию распределения F(x).
Если x  0, то F(x)=P(X< x)=0
0, то F(x)=P(X< x)=0
Если 0< x  1, то F(x)= p0=1/35
1, то F(x)= p0=1/35
Если 1< x  2, то F(x)= p0+ p1=1/35+12/35=13/35
2, то F(x)= p0+ p1=1/35+12/35=13/35
Если 2< x  3, то F(x)= p0+ p1+ p2=31/35
3, то F(x)= p0+ p1+ p2=31/35
Если x> 3, то F(x)= p0+ p1+ p2+ p3=1
Таким образом,
F(x)= 
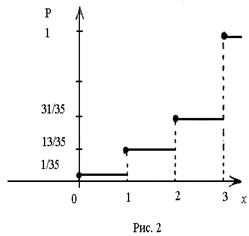
Функция распределения изображена на рисунке 2

Числовыми характеристиками дискретной случайной величины служат математическое ожидание, дисперсия и среднее квадратичное отклонение.
Математиеским ожиданием M [ X ] дискретной случайной величины X называют симму произведений всех ее возможных значений xi на их вероятности
M[X]= 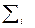 xi
xi  pi (1)
pi (1)
Свойства математического ожидания:
1) если с – постоянная, то M [ c ] =c;
2) M[c  X]=c
X]=c  M[X];
M[X];
3) если X и Y – независимы, то M[X  Y]=M[X]
Y]=M[X]  M[Y];
M[Y];
4) M[X+Y]=M[X]+M[Y].
Дисперсией (рассеянием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
D[X]=M[(X-M[X])  ]. (2)
]. (2)
Дисперсию можно вычислять по формуле
D[X] =M[X  ]-M[X]
]-M[X]  . (2’)
. (2’)
Свойства дисперсии:
1) Если c – постоянная, то D [c]=0;
2) D [c X ]=c  D[X];
D[X];
3) если X и Y – независимы, то D [ X+Y ]= D [ X ]+ D [ Y ]
Дисперсия характеризует меру рассеяния значений случайной величины вокруг математического ожидания.
Средним квадратическим отклонением случайной величины X называется квадратный корень из дисперсии
σ [ X ]= 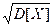 (3)
(3)
2.2 Задача. Три стрелка независимо друг от друга 1 раз стреляют по одной цели. Вероятность попадания первого стрелка в цель равна 0, 7, второго – 0, 8, третьего – 0, 9. Найти математическое ожидание Z числа попаданий в цель.
Решение. Пусть X i– число попаданий в цель для i – го стрелка (i =1, 2, 3), очевидно
Xi 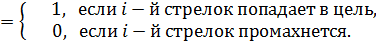
Z=X1+X2+X3, M[Z]=M[X1+X2+X3]=M[X1]+M[X2]+M[X3]
| X1 | ||
| p | 0, 3 | 0, 7 |
| X2 | ||
| p | 0, 2 | 0, 8 |
| X3 | ||
| p | 0, 1 | 0, 9 |
M[X1]=0, 7; M[X2]=0, 8; M[X3]=0, 9 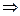
M[Z]= M[X1+ X2+ X3]=0, 7+0, 8+0, 9=2, 4.
Решите задачи самостоятельно:
2.3 Найдите математическое ожидание, дисперсию и построить функцию распределения дискретной случайной величины, заданной законом распределения
| X | -2 | |||
| p | 0, 1 | 0, 4 | 0, 3 | 0, 2 |
(3, 1; 13, 89)
2.4 Случайная величина X может принимать 4 возможных значения: 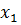 =1,
=1, 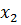 =3,
=3, 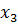 =4,
=4, 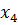 =6. Вероятности появления первых трех возможных значений равны
=6. Вероятности появления первых трех возможных значений равны 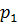 = 0, 1,
= 0, 1,  = 0, 4,
= 0, 4,  =0, 2. Написать закон распределения случайной величины X.
=0, 2. Написать закон распределения случайной величины X.
2.5 Дискретная случайная величина X принимает три возможных значения: 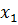 = 2 с вероятностью
= 2 с вероятностью 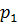 = 0, 3,
= 0, 3, 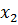 = 4 с вероятностью
= 4 с вероятностью  = 0, 4 и значение
= 0, 4 и значение 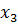 с вероятностью
с вероятностью  . Найти
. Найти 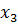 и
и  , зная, что M[X] =5. (9, 33; 0, 3).
, зная, что M[X] =5. (9, 33; 0, 3).
2.6 Одновременно бросают три игральные кости. Найди математическое ожидание числа таких бросаний, в каждом из которых выпадет ровно 2 шестерки, если общее число бросаний равно 15. (≈ 1, 042)
2.7 Найти математическое ожидание М[X] и дисперсию D [ X ]числа X лотерейных билетов, на которые выпадут выигрыши, если приобретено 100 билетов, а вероятность выигрыша на каждый билет равна 0.05. (5; 4, 75)
2.8 Найти дисперсию дискретной случайной величины X -числа отказов элементов некоторого устройства в 20 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0.3. (4.2)
2.9 Дискретная случайная величина X имеет только два возможных значения 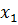 и
и 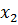 , причем |
, причем |  > |
> | 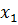 |. Вероятность того, что X примет значение
|. Вероятность того, что X примет значение 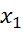 равна 0, 3. Написать закон распределения величины X, если известно, что М[Х] = 3, 4; D [ X ]= 0, 84.
равна 0, 3. Написать закон распределения величины X, если известно, что М[Х] = 3, 4; D [ X ]= 0, 84.
2.10 В партии из 5 деталей имеется 3 стандартных. Наудачу отобраны 2 детали, Составить закон распределений дискретной случайной величины X - числа стандартных деталей среди отобранных.
2.11 Чемуравно математическое ожидание суммы числа очков, которые могут выпасть при одном бросании трех игральных костей? (21/2).
2.12 Дискретная случайная величина X - число мальчиков в семьях с 5 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения Х; б) постройте многоугольник распределения; в ) найдите вероятности событий; А - в семье не менее 2, но не более 3 мальчиков; В - не более 3 мальчиков; С - более одного мальчика. (5/8; 13/16; 13/16).
2.13 С вероятностью попадания при одном выстреле 0, 7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов, Дискретная случайная величина X - числопромахов, в) Найдите закон распределения X. б) Постройте многоугольник распределения. в) Найдите вероятности событий: X < 2; X ≤ 3; 1 < X ≤ 3. (0, 91; 0, 9919; 0, 0819)
2.14 В коробке имеются 7 карандашей, из которых 4 - красные. Из этой коробки наудачу извлекаются 3 карандаша. а) Найдите закон распределения случайной величины X, равной числу красных карандашей в выборке. б) Постройте многоугольник распределения. в) Найдите вероятность события: 0 < X ≤ 2. (6/7)
2.15 Из 25 контрольных работ, среди которых 5 оценены на " отлично", наугад извлекают 3 работы. Найдите закон распределения, математическое ожидание и дисперсию случайной величины X, равной числу оцененных на " отлично" работ среди извлеченных. Чему равна вероятность события X > 0? (0, 6; 0, 44; 58/115)
2.16 Имеются 5 ключей, из которых только один подходит к замку. Найдите закон распределения, математическое ожидание и дисперсию случайной величины X, равной числу проб при открывании замка, если испробованный ключ в последующих опробованиях не участвует. (3; 2)
2.17 В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 2 детали. Найдите закон распределения, математическое ожидание к дисперсии случайной величины X, равной числу стандартных деталей в выборке. (1, 6; 0, 2855)
2.18 Бросается игральная кость до первого выпадения шестерки. Случайная величина X равна количеству бросаний кости. Найдите закон распределения случайной величины X и вероятность события X ≤ 5. (0, 335)
2.19 На пути движения автомобиля 6 светофоров, каждый из них или разрешает, ил» запрещает дальнейшее движение с вероятностью 0, 5. Найдите закон распределения, математическое ожидание и дисперсию случайной величины X, равной числу светофоров, пройденных автомобилем до первой остановки. (0, 656; 1, 788)
2.20 Вероятность изготовления нестандартной детали 0, 1. Изпартии контролер берет деталь и проверяет ее на стандартность, Если деталь оказывается нестандартной, то дальнейшие испытания прекращаются, а партия вся задерживается. Если же деталь окажется стандартной, то контролер берет следующую и т.д., но всего он проверяет не более 5 деталей. Найдите закон распределения, математическое ожидание и дисперсию случайной величины X, равной числу проверяемых стандартных деталей. (4, 095; 1, 9889)
2.21 Производятся последовательные испытания 5 приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Найдите закон распределения и функцию распределения случайного числа испытанных приборов, если вероятность выдержать испытания для каждого прибора равна 0.9,
2; 22 Даны все возможные значения дискретной случайной величины X: х1 = 1, x2 = 2, х3 = 3, а также известны М[Х] = 2, 3, M[X2] = 5.9. Найдите закон распределения величины X.