
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние. Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака
|
|
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
 ,
,
где XMe – нижняя граница медианного интервала;
hMe – его величина;
(Sum m)/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
SMe-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
В нашем примере могут быть получены даже три медианных значения – исходя из признаков количества предприятий, объема продукции и общей суммы затрат на производство:

Таким образом, у половины предприятий уровень себестоимость единицы продукции превышает 125, 19 тыс. руб., половина всего объема продукции производится с уровнем затрат на изделие больше 124, 79 тыс. руб. и 50 % общей суммы затрат образуется при уровне себестоимости одного изделия выше 125, 07 тыс. руб. Заметим также, что наблюдается некоторая тенденция к росту себестоимости, так как Ме2 = 124, 79 тыс. руб., а средний уровень равен 123, 15 тыс. руб.
При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как
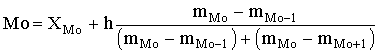 ,
,
где ХMo – нижнее значение модального интервала;
mMo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
mMo-1 – то же для интервала, предшествующего модальному;
mMo+1 – то же для интервала, следующего за модальным;
h – величина интервала изменения признака в группах.
Для нашего примера можно рассчитать три модальных значения исходя из признаков числа предприятий, объема продукции и суммы затрат. Во всех трех случаях модальный интервал один и тот же, так как для одного и того же интервала оказываются наибольшими и число предприятий, и объем продукции, и общая сумма затрат на производство:
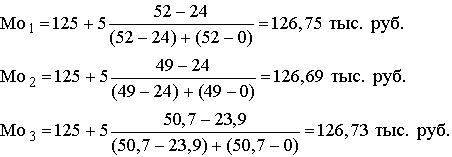
Таким образом, чаще всего встречаются предприятия с уровнем себестоимости 126, 75 тыс. руб., чаще всего выпускается продукция с уровнем затрат 126, 69 тыс. руб., и чаще всего затраты на производство объясняются уровнем себестоимости в 123, 73 тыс. руб.