
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 16: Застосування методів диференціального числення до розв’язування деяких економічних задач.
|
|
Оскільки похідна характеризує швидкість (миттєву, тобто, в певний момент) зміни значень функції, то цілком природньо, що диференціальне числення застосовується при моделюванні динамічних процесів. Окрім того, методи диференціального числення використовуються у дослідженнях характеру поведінки функцій – моделей явищ, особливо, їх екстремальних (або оптимальних) значень. При моделюванні економічних явищ функції – моделі часто називають кривими зростання, першу похідну (що характеризує швидкість) називають темпом росту, а другу похідну (що характеризує прискорення) – темпом приросту.
В економіці широко використовуються поняття середніх та граничних (маржинальних) витрат, доходу тощо. Розберемо ці поняття. Нехай функція  встановлює залежність витрат
встановлює залежність витрат 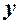 від кількості
від кількості 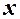 випущеної продукції. Тоді функція
випущеної продукції. Тоді функція  визначає величину середніх (або питомих) витрат, тобто, визначає витрати на виробництво однієї одиниці продукції при даному об’ємові випуску
визначає величину середніх (або питомих) витрат, тобто, визначає витрати на виробництво однієї одиниці продукції при даному об’ємові випуску 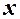 . Припустимо, що кількість випуску продукції змінилось на
. Припустимо, що кількість випуску продукції змінилось на 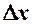 . Тоді витрати виробництва змінились на величину
. Тоді витрати виробництва змінились на величину 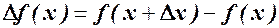 , а середні – на
, а середні – на  . Якщо перейти до границі, дістанемо
. Якщо перейти до границі, дістанемо 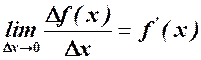 - граничні витрати (або швидкість зміни витрат). Відзначимо, що граничні витрати приблизно дорівнюють витратам на випуск наступної
- граничні витрати (або швидкість зміни витрат). Відзначимо, що граничні витрати приблизно дорівнюють витратам на випуск наступної 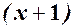 -ої одиниці продукції. Аналогічно можна розглянути, наприклад, граничний дохід і т.і.
-ої одиниці продукції. Аналогічно можна розглянути, наприклад, граничний дохід і т.і.
Приклад. Економічним відділом заводу встановлено, що при виробництві 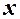 одиниць продукції щотижневі витрати
одиниць продукції щотижневі витрати  визначаються залежністю
визначаються залежністю 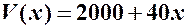 (грн), а дохід
(грн), а дохід 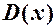 - залежністю
- залежністю 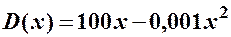 (грн). Щотижня завод випускає 3000 одиниць продукції, але бажає збільшити випуск до 3100 одиниць. Обчислити прирости витрат, доходу та прибутку. Знайти величину середнього приросту прибутку. Прокоментувати отримані результати.
(грн). Щотижня завод випускає 3000 одиниць продукції, але бажає збільшити випуск до 3100 одиниць. Обчислити прирости витрат, доходу та прибутку. Знайти величину середнього приросту прибутку. Прокоментувати отримані результати.
Розв’язування. Обчислюємо прирости витрат та доходу при 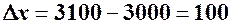 :
:
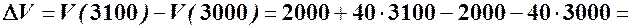
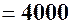 (грн).
(грн).

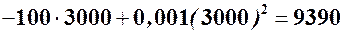 (грн).
(грн).
Приріст прибутку обчислюємо як різницю приростів доходу та витрат:
 (грн).
(грн).
Зауважимо, що цей приріст можна знайти, визначивши функцію прибутку:
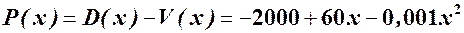 (грн).
(грн).
Величина середнього приросту прибутку становить 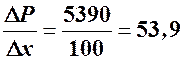 (грн).
(грн).
Отже, при збільшенні випуску з 3000 до 3100 одиниць дохід зросте на 9390 грн, витрати – на 4000 грн, загальний дохід – на 5390 грн. Дохід від випуску кожної із наступних 100 одиниць продукції в середньому становить 53, 9 грн.
Приклад. Функція витрат  (грн) підприємства при виробництві
(грн) підприємства при виробництві 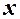 одиниць продукції має вигляд
одиниць продукції має вигляд 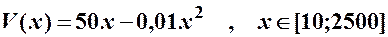 . Знайти при виробництві
. Знайти при виробництві 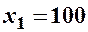 та
та  одиниць продукції: а) середні витрати; б) додаткові витрати на виробництво одиниці додаткової продукції; в) граничні (маржинальні) витрати. Охарактеризувати отримані результати.
одиниць продукції: а) середні витрати; б) додаткові витрати на виробництво одиниці додаткової продукції; в) граничні (маржинальні) витрати. Охарактеризувати отримані результати.
Розв’язування. а) Визначимо функцію середніх витрат:
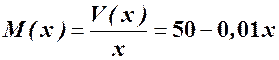 . Обчислюємо середні витрати при виробництві
. Обчислюємо середні витрати при виробництві 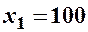 та
та  одиниць продукції:
одиниць продукції:
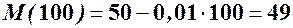 (гр.од);
(гр.од);  (гр.од).
(гр.од).
б) Додаткові витрати на виробництво додаткової одиниці продукції:
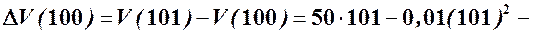
 (гр.од).
(гр.од).
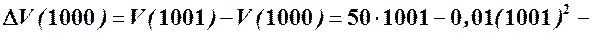
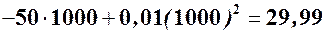 (гр.од).
(гр.од).
в) Для знаходження граничних (маржинальних) витрат спочатку знайдемо похідну функції витрат  , а потім їх відповідні значення:
, а потім їх відповідні значення:
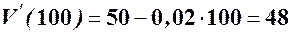 (гр.од);
(гр.од);
 (гр.од).
(гр.од).
Приклад показує, що при збільшенні випуску середні (питомі) витрати (або витрати на одиницю продукції) зменшуються. Окрім того, бачимо, що граничні витрати приблизно дорівнюють витратам на випуск наступної одиниці продукції.
Економісти часто оперують поняттям еластичності функції. Як відомо, еластичність функції  відносно змінної
відносно змінної 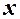 є показник
є показник  , який приблизно дорівнює процентній зміні значень функції при зміні аргумента на 1%.
, який приблизно дорівнює процентній зміні значень функції при зміні аргумента на 1%.
Приклад. На ринку деякого товару залежності обсягів (в одиницях) попиту 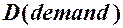 та пропозиції
та пропозиції 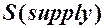 від ціни
від ціни 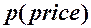 за одиницю товару визначаються формулами:
за одиницю товару визначаються формулами:  . Знайти еластичності попиту
. Знайти еластичності попиту 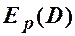 та пропозиції
та пропозиції 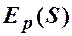 відносно рівноважної ціни
відносно рівноважної ціни  . Охарактеризувати отримані результати.
. Охарактеризувати отримані результати.
Розв’язування. Спочатку знаходимо рівновжну ціну  , розв’язуючи рівняння:
, розв’язуючи рівняння:  , допустимим розв’язком якого, очевидно, є
, допустимим розв’язком якого, очевидно, є 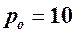 .
.
Знаходимо еластичності: попиту  ; при
; при 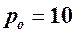 дістанемо
дістанемо 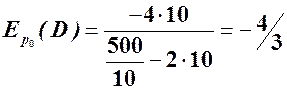 ;
;
пропозиції 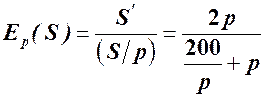 ; при
; при 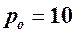 дістанемо
дістанемо 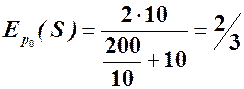 .
.
Результати свідчать про те, що, наприклад, при зростанні ціни від рівноважної 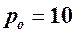 на 1% попит зменшиться приблизно на 4/3%, а пропозиція зросте приблизно на 2/3%.
на 1% попит зменшиться приблизно на 4/3%, а пропозиція зросте приблизно на 2/3%.
Розглянемо деякі оптимізаційні задачі (задачі пошуку екстремальних значень функцій).
Приклад. Функція повних витрат має вигляд:  , де
, де 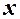 - обсяг виробництва продукції. При якому обсязі виробництва середні витрати будуть мінімальними? Якими будуть граничні витрати при знайденому обсязі виробництва?
- обсяг виробництва продукції. При якому обсязі виробництва середні витрати будуть мінімальними? Якими будуть граничні витрати при знайденому обсязі виробництва?
Розв’язування. Насамперед визначимо функцію середніх витрат:
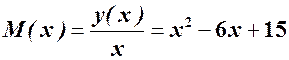 , область визначення якої (згідно з умовами задачі)
, область визначення якої (згідно з умовами задачі) 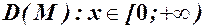 . Дослідимо функцію на екстремум. Похідна
. Дослідимо функцію на екстремум. Похідна 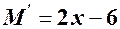 визначена для будь-яких
визначена для будь-яких 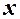 , тому серед критичних будуть лише точки, в яких похідна дорівнює нулю, тобто
, тому серед критичних будуть лише точки, в яких похідна дорівнює нулю, тобто 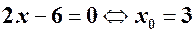 - критична точка. Оскільки похідна другого порядку
- критична точка. Оскільки похідна другого порядку  , то за теоремою (друга достатня умова екстремума)
, то за теоремою (друга достатня умова екстремума)  - точка мінімума функції середніх витрат, причому цей локальний мінімум є і глобальним (найменше значення функції на
- точка мінімума функції середніх витрат, причому цей локальний мінімум є і глобальним (найменше значення функції на  . Отже, мінімальні середні витрати становлять
. Отже, мінімальні середні витрати становлять 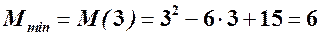 при випуску 3 одиниць продукції. Граничні витрати при даному обсязі випуску, очевидно, дорівнюють
при випуску 3 одиниць продукції. Граничні витрати при даному обсязі випуску, очевидно, дорівнюють 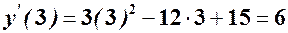 .
.
Приклад. Компанія виготовляє і реалізує вироби по 2 грн за кожний. Дослідженнями встановлено, що сума  (грн) загальних щотижневих витрат на виробництво
(грн) загальних щотижневих витрат на виробництво 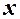 (тисяч штук) визначається залежністю:
(тисяч штук) визначається залежністю: 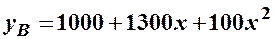 (грн). Визначити та дослідити залежність щотижневого прибутку
(грн). Визначити та дослідити залежність щотижневого прибутку 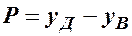 (грн), де
(грн), де 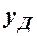 (грн) – доход від реалізації виробленої продукції. При яких об’ємах виробництва забезпечується: а) беззбитковість; б) максимальний прибуток?
(грн) – доход від реалізації виробленої продукції. При яких об’ємах виробництва забезпечується: а) беззбитковість; б) максимальний прибуток?
Розв’язування. Визначаємо функцію щотижневого прибутку:
 із областю визначення
із областю визначення 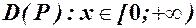 .
.
Для знаходження об’ємів виробництва, які б забезпечували беззбитковість, потрібно розв’язати рівняння  . Таким чином, беззбитковість забезпечується при випуску від 2 до 5 тисяч одиниць продукції (оскільки при
. Таким чином, беззбитковість забезпечується при випуску від 2 до 5 тисяч одиниць продукції (оскільки при 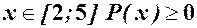 , див. рис.).
, див. рис.).
Для знаходження максимального прибутка проведемо дослідження на екстремум. Похідна  всюди визначена, тому для знаходження критичних точок розв’язуємо рівняння
всюди визначена, тому для знаходження критичних точок розв’язуємо рівняння 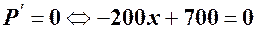 . Критична точка
. Критична точка  є точкою максимума, оскільки
є точкою максимума, оскільки  . Отже, максимальний прибуток
. Отже, максимальний прибуток  (грн) досягається при випуску 3500 одиниць продукції.
(грн) досягається при випуску 3500 одиниць продукції.
Приклад. Продуктивність праці робітників цеху визначається функцією  , де
, де 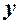 - обсяг продукції, виготовленої за одиницю часу,
- обсяг продукції, виготовленої за одиницю часу, 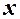 (год.) - час, що відраховується від початку роботи. Визначити момент часу, в який продуктивність праці максимальна, і знайти цю максимальну продуктивність.
(год.) - час, що відраховується від початку роботи. Визначити момент часу, в який продуктивність праці максимальна, і знайти цю максимальну продуктивність.
Розв’язування. Знаходимо найбільше значення функції  на замкненому проміжку
на замкненому проміжку  . Знаходимо похідну та її критичні точки, що належать проміжку:
. Знаходимо похідну та її критичні точки, що належать проміжку:
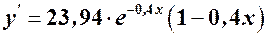 . Оскільки показникова функція набуває лише додатних значень, то критична точка визначається із умови
. Оскільки показникова функція набуває лише додатних значень, то критична точка визначається із умови  . Критична точка
. Критична точка  . Серед значень
. Серед значень 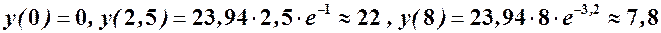
очевидно, найбільшим є  . Отже, максимальна продуктивність становить
. Отже, максимальна продуктивність становить 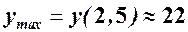 одиниць продукції за годину і досягається через 2, 5 години після початку робочої зміни.
одиниць продукції за годину і досягається через 2, 5 години після початку робочої зміни.