Критерий минимаксного риска Сэвиджа

Рассчитаем матрицу рисков. Заполнять ее лучше по столбцам. В каждом столбце находим максимальный элемент и вы читаем из него все остальные элементы столбца, результаты записываем на соответствующих местах.

Вот как рассчитывается первый столбец. Максимальный элемент в первом столбце: , значит по формуле :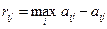

;

;

.

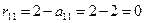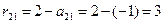Рассчитаем второй столбец матрицы рисков. Максимальный элемент во втором столбце: 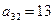, значит:

;

;

.

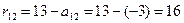Рассчитаем третий столбец матрицы рисков. Максимальный элемент в третьем столбце: 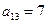, значит:

;

;

.

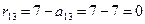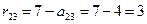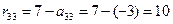Таким образом, матрица рисков имеет вид (в каждом столбце на месте максимального элемента платежной матрицы должен стоять ноль):

Дополним матрицу рисков рассчитанными значениями критерия W_i – в каждой строке выбираем максимальный элемент ():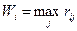

;

;

;

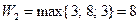Найденные значения заносим в столбец (W_i) и выбираем минимальное 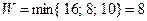, значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.

Вывод:

1) Стратегия А1 (продавать сразу после уборки) не является оптимальной ни по одному из критериев.

2) Стратегия А2 (продавать в зимние месяцы) является оптимальной согласно критериям недостаточного основания Лапласа, максиминного критерия Вальда и минимаксного критерия Сэвиджа.

3) Стратегия А3 (продавать в весенние месяцы) является оптимальной согласно критериям Байеса, пессимизма-оптимизма Гурвица, Ходжа-Лемана.