
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Некоторые комбинаторные формулы
|
|
Как правило, подсчет вероятностей по классической формуле сводится к решению
чисто комбинаторных задач. Приведем наиболее часто используемые комбинаторные
формулы.
1. Число перестановок. Пусть n элементов а 1, a 2, …, аn надо разместитьпо n позициям.
Сколькими способами это можно сделать?
В первую позицию можно поместить любой из этих элементов
(n различных вариантов), во вторую - любой из (n – 1)-го оставшегося, для заполнения
третьей позиции существует только (n – 2) варианта и т.д. Общее число различных
перестановок равно n (n – 1)(n – 2) … 1 = n!
2. Число размещений. Пусть теперь m элементов из n (m < n) надо разместить по m
позициям. Такие комбинации называются размещениями.
Общее число размещений из n элементов по m обозначается
Anm и равняется n (n –1)(n – 2) … (n – m + 1), так как существует n вариантов разместить элемент в первой
позиции, (n – 1) вариантов - во второй, …, (n – m + 1) вариантов - в m -й позиции. Итак,

.
3. Число сочетаний. Рассмотрим выборки из n элементов по m (m < n), отличающиеся
только составом, без учета порядка, в котором они выбираются. Такие комбинации
называются сочетаниями.
Поскольку m элементов можно переставлять m! способами, общее число сочетаний
Cnm будет в m! раз меньше, чем общее число размещений:

4. Число размещений с повторениями. Теперь, выбирая элемент из
n элементов, будем запоминать его номер, а элемент возвращать обратно. Комбинации,
которые могут получиться при таком m -кратном выборе, называются размещениями с
повторениями. Общее число размещений с повторениями обозначается
% Anm и, очевидно, равняется nm.
5. Число сочетаний с повторениями. Выборку из n элементов по m с возвращением
можно проводить и без учета порядка, в котором элементы выбираются. Общее число
получающихся при таком выборе сочетаний с повторениями
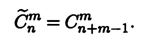
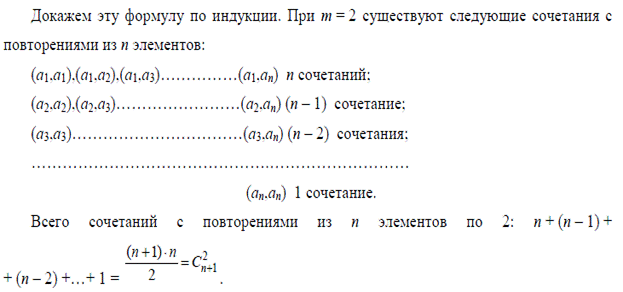

|