
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЗАДАНИЕ 1. Применяя метод интегрирования по частям, найти:
|
|
Применяя метод интегрирования по частям, найти:
1.1 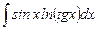 ;
;
1.2 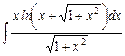 ;
;
1.3 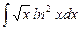 ;
;
1.4 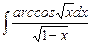 ;
;
1.5 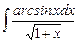 ;
;
1.6 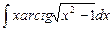 ;
;
1.7  ;
;
1.8 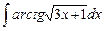 ;
;
1.9 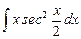 ;
;
1.10  ;
;
1.11 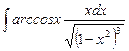 ;
;
1.12 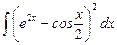 ;
;
1.13 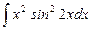 ;
;
1.14 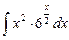 ;
;
1.15 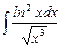 ;
;
1.16 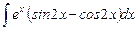 ;
;
1.17 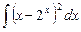 ;
;
1.18 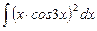 ;
;
1.19 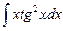 ;
;
1.20 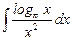 ;
;
1.21 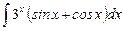 ;
;
1.22 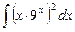 ;
;
1.23 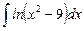 ;
;
1.24 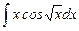 ;
;
1.25 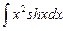 .
.
ЗАДАНИЕ 2
Найти интегралы от рациональных дробей:
2.1 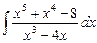 ;
;
2.2 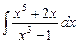 ;
;
2.3  ;
;
2.4 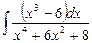 ;
;
2.5 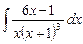 ;
;
2.6 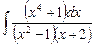 ;
;
2.7 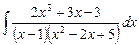 ;
;
2.8 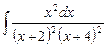 ;
;
2.9 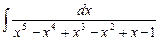 ;
;
2.10 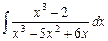 ;
;
2.11  ;
;
2.12 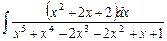 ;
;
2.13 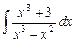 ;
;
2.14 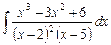 ;
;
2.15  ;
;
2.16 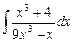 ;
;
2.17  ;
;
2.18 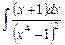 ;
;
2.19 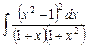 ;
;
2.20 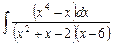 ;
;
2.21 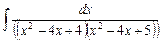 ;
;
2.22 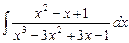 ;
;
2.23 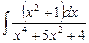 ;
;
2.24 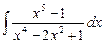 ;
;
2.25 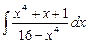 .
.
ЗАДАНИЕ 3
Найти интегралы от иррациональных функций:
3.1 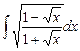 ;
;
3.2 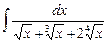 ;
;
3.3 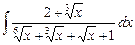 ;
;
3.4 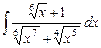 ;
;
3.5 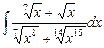 ;
;
3.6 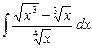 ;
;
3.7 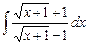 ;
;
3.8  ;
;
3.9 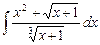 ;
;
3.10 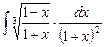 ;
;
3.11 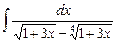 ;
;
3.12 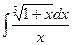 ;
;
3.13 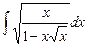 ;
;
3.14 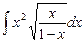 ;
;
3.15 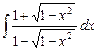 ;
;
3.16 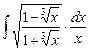 ;
;
3.17 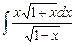 ;
;
3.18 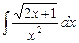 ;
;
3.19 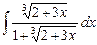 ;
;
3.20 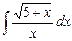 ;
;
3.21 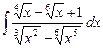 ;
;
3.22  ;
;
3.23 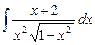 ;
;
3.24 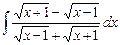 ;
;
3.25 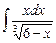 .
.
ЗАДАНИЕ 4
Найти интеграл от дифференциального бинома:
4.1 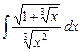 ;
;
4.2 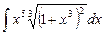 ;
;
4.3  ;
;
4.4 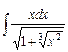 ;
;
4.5 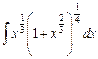 ;
;
4.6 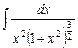 ;
;
4.7 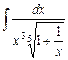 ;
;
4.8  ;
;
4.9 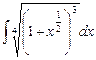 ;
;
4.10  ;
;
4.11 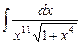 ;
;
4.12 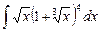 ;
;
4.13 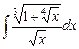 ;
;
4.14  ;
;
4.15 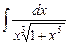 ;
;
4.16 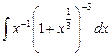 ;
;
4.17 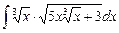 ;
;
4.18 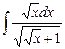 ;
;
4.19 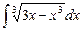 ;
;
4.20 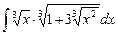 ;
;
4.21 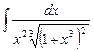 ;
;
4.22 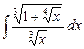 ;
;
4.23 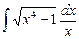 ;
;
4.24 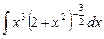 ;
;
4.25 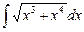 .
.
ЗАДАНИЕ 5
Применяя подстановки Эйлера, найти:
5.1 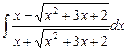 ;
;
5.2  ;
;
5.3  ;
;
5.4 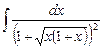 ;
;
5.5 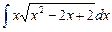 ;
;
5.6  ;
;
5.7 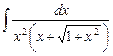 ;
;
5.8 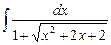 ;
;
5.9 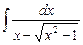 ;
;
5.10 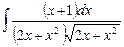 ;
;
5.11  ;
;
5.12 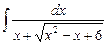 ;
;
5.13 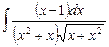 ;
;
5.14 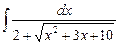 ;
;
5.15 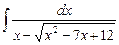 ;
;
5.16 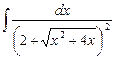 ;
;
5.17 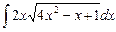 ;
;
5.18 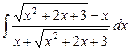 ;
;
5.19 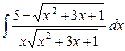 ;
;
5.20 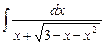 ;
;
5.21 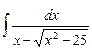 ;
;
5.22 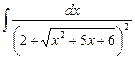 ;
;
5.23 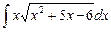 ;
;
5.24 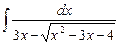 ;
;
5.25 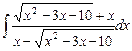 .
.
ЗАДАНИЕ 6
Найти:
6.1 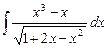 ;
;
6.2  ;
;
6.3 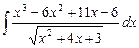 ;
;
6.4 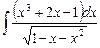 ;
;
6.5 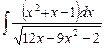 ;
;
6.6  ;
;
6.7 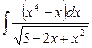 ;
;
6.8  ;
;
6.9 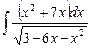 ;
;
6.10 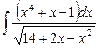 ;
;
6.11 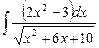 ;
;
6.12 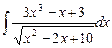 ;
;
6.13 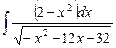 ;
;
6.14 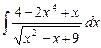 ;
;
6.15 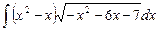 ;
;
6.16 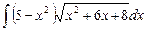 ;
;
6.17 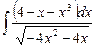 ;
;
6.18 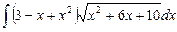 ;
;
6.19 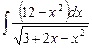 ;
;
6.20 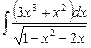 ;
;
6.21 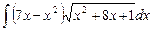 ;
;
6.22 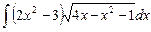 ;
;
6.23 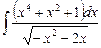 ;
;
6.24 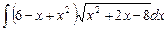 ;
;
6.25 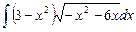 .
.
ЗАДАНИЕ 7
Найти интегралы от тригонометрических функций:
7.1  ;
;
7.2 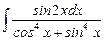 ;
;
7.3 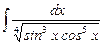 ;
;
7.4 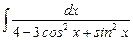 ;
;
7.5 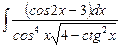 ;
;
7.6 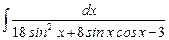 ;
;
7.7 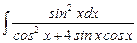 ;
;
7.8 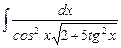 ;
;
7.9 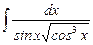 ;
;
7.10 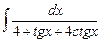 ;
;
7.11 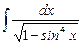 ;
;
7.12  ;
;
7.13 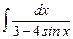 ;
;
7.14 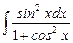 ;
;
7.15 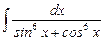 ;
;
7.16  ;
;
7.17 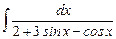 ;
;
7.18 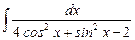 ;
;
7.19 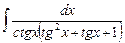 ;
;
7.20 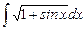 ;
;
7.21  ;
;
7.22 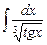 ;
;
7.23 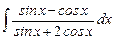 ;
;
7.24 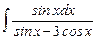 ;
;
7.25 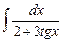 .
.
ЗАДАНИЕ 8
Найти интегралы от гиперболических функций:
8.1 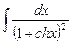 ;
;
8.2 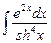 ;
;
8.3 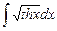 ;
;
8.4 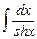 ;
;
8.5 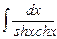 ;
;
8.6  ;
;
8.7  ;
;
8.8 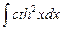 ;
;
8.9 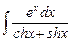 ;
;
8.10 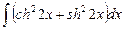 ;
;
8.11 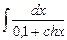 ;
;
8.12 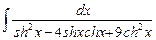 ;
;
8.13 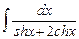 ;
;
8.14  ;
;
8.15  ;
;
8.16  ;
;
8.17 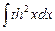
8.18 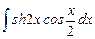 ;
;
8.19 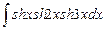 ;
;
8.20 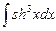 ;
;
8.21 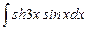 ;
;
8.22 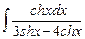 ;
;
8.23 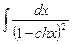 ;
;
8.24 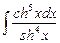 ;
;
8.25 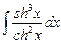 .
.
ЗАДАНИЕ 9
Найти интегралы от трансцендентных функций:
9.1 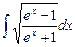 ;
;
9.2 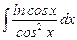 ;
;
9.3  ;
;
9.4 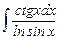 ;
;
9.5 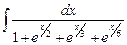 ;
;
9.6 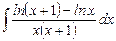 ;
;
9.7 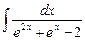 ;
;
9.8 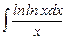 ;
;
9.9  ;
;
9.10 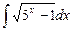 ;
;
9.11  ;
;
9.12 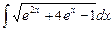 ;
;
9.13 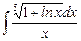 ;
;
9.14  ;
;
9.15 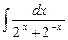 ;
;
9.16 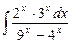 ;
;
9.17 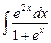 ;
;
9.18 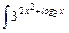 dx;
dx;
9.19 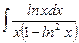 ;
;
9.20 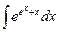 ;
;
9.21 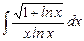 ;
;
9.22  ;
;
9.23 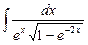 ;
;
9.24 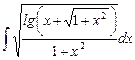 ;
;
9.25 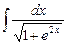 .
.
ЗАДАНИЕ 10
Вычислить, пользуясь формулой Ньютона–Лейбница:
10.1 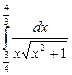 ;
;
10.2 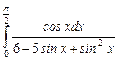 ;
;
10.3  ;
;
10.4 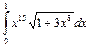 ;
;
10.5 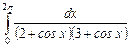 ;
;
10.6 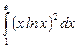 ;
;
10.7 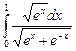 ;
;
10.8 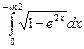 ;
;
10.9  ;
;
10.10 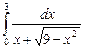 ;
;
10.11 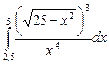 ;
;
10.12 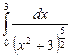 ;
;
10.13 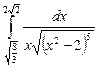 ;
;
10.14  ;
;
10.15 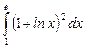 ;
;
10.16 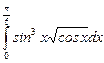 ;
;
10.17  ;
;
10.18 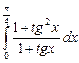 ;
;
10.19 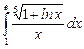 ;
;
10.20 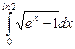 ;
;
10.21 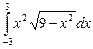 ;
;
10.22 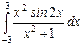 ;
;
10.23  ;
;
10.24 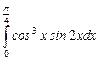 ;
;
10.25 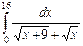 .
.
ЗАДАНИЕ 11
Исследовать на сходимость несобственные интегралы первого рода:
11.1 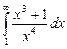 ;
;
11.2 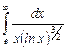 ;
;
11.3 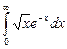 ;
;
11.4 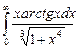 ;
;
11.5 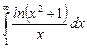 ;
;
11.6 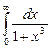 ;
;
11.7 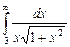 ;
;
11.8 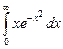 ;
;
11.9 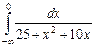 ;
;
11.10 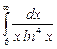 ;
;
11.11  ;
;
11.12 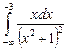 ;
;
11.13 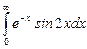 ;
;
11.14 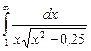 ;
;
11.15 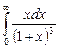 ;
;
11.16 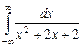 ;
;
11.17 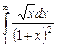 ;
;
11.18 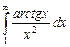 ;
;
11.19 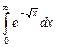 ;
;
11.20 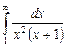 ;
;
11.21 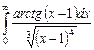 ;
;
11.22 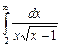 ;
;
11.23 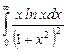 ;
;
11.24 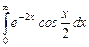 ;
;
11.25 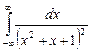 .
.
ЗАДАНИЕ 12
Исследовать на сходимость несобственные интегралы второго рода:
12.1  ;
;
12.2 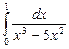 ;
;
12.3 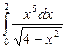 ;
;
12.4  ;
;
12.5 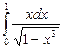 ;
;
12.6 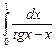 ;
;
12.7 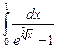 ;
;
12.8 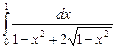 ;
;
12.9 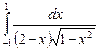 ;
;
12.10 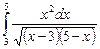 ;
;
12.11 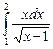 ;
;
12.12 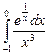 ;
;
12.13 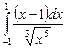 ;
;
12.14 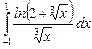 ;
;
12.15 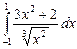 ;
;
12.16 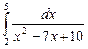 ;
;
12.17 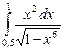 ;
;
12.18 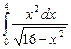 ;
;
12.19 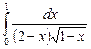 ;
;
12.20 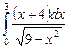 ;
;
12.21 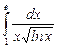 ;
;
12.22 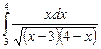 ;
;
12.23 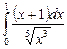 ;
;
12.24 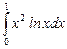 ;
;
12.25 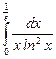 .
.