Задание 13

Найти, применяя определенный интеграл:

13.1 Площадь фигуры, ограниченной линиям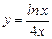и

и .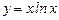

13.2 Площадь фигуры, ограниченной линиями , , .

13.3 Площадь фигуры, ограниченной осью ординат и кривыми , .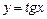

13.4 Площадь области, ограниченной кривой .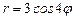

13.5 Площадь области, ограниченной гипоциклоидой

.

13.6 Площадь области, ограниченной линиями

, .

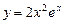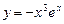13.7 Площади областей, на которые парабола 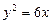делит окружность .

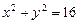13.8 Площадь области, ограниченной кардиоидой 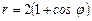и расположенной справа от прямой .

13.9 Площадь области, ограниченной эллипсом .

13.10 Площадь области, заключенной между линиями и .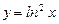

13.11 Площадь области, ограниченной кривыми 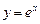, 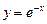и прямой .

13.12 Площадь области, ограниченной эллипсом , справа от прямой .

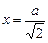13.13 Площадь области, ограниченной параболой 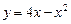и прямой .

13.14 Площадь области, ограниченной кривыми , .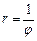

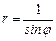
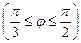13.15 Площадь области, ограниченной кривой .

13.16 Площадь области, ограниченной параболам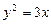и и .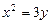

13.17 Площадь области, ограниченной параболой 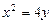и кривой .

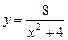13.18 Площадь области, ограниченной кривой 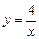, осью Ох и прямыми х=2 и х=4.

13.19 Площадь области, ограниченной линиям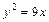и и .

13.20 Площадь области, ограниченной линией , где .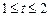

13.21 Площадь области, ограниченной линией

.

13.22 Площадь области, ограниченной .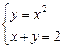

13.23 Площадь области, ограниченной линиями , у=4, х=0.

13.24 Площадь области, ограниченной линиями

, х=1, , .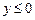

13.25 Площадь области, ограниченной линиями 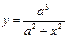, у=0.