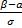Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 35.
|
|
Нормальное распределение. Плотность распределения. Функция распределения. Правило трех сигм. Числовые характеристики нормального распределения.
Нормальное распределение – распределение вероятности непрерывной случайной величины, котор. Описыв-ся ф:
F(x) = 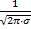 · e-(х-а)вквадрате/2ɢ вквадрате
· e-(х-а)вквадрате/2ɢ вквадрате
Нормальное распределение определяется 2-мя параметреми: а и 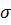 . Можно показать, что а представляет ничто иное, как математическое ожидание х.
. Можно показать, что а представляет ничто иное, как математическое ожидание х.
A = M[X] = 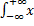 ·
· 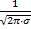 · e-(х-а)вквадрате/2ɢ вквадрате dx,
· e-(х-а)вквадрате/2ɢ вквадрате dx, 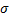 – среднее квадратичное отклонение случайной величины х. Функция распределения для нормального закона распределения может быть найдена так:
– среднее квадратичное отклонение случайной величины х. Функция распределения для нормального закона распределения может быть найдена так:
F(x) = 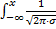 · e-(х-а)вквадрате/2ɢ вквадрате dx =
· e-(х-а)вквадрате/2ɢ вквадрате dx =  = 0, 5+
= 0, 5+ 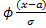 , где
, где 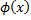 -функция Лапласса.
-функция Лапласса.
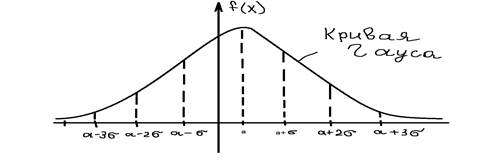
Изменение величины а не изменяет форму кривой Гауса. С увеличением а кривая сдвигается вдоль оси по х вправо с уменьшением влево. При изменении 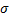 форма кривой изменяется, при возрастании
форма кривой изменяется, при возрастании 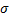 максимальная координата кривой убывает, кривая становится более плоской, т.е прижимается к оси. При убывании
максимальная координата кривой убывает, кривая становится более плоской, т.е прижимается к оси. При убывании 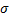 становится островерхой, т.е растягивается по оси у.
становится островерхой, т.е растягивается по оси у.
Нормальный закон распределения проявляется во всех случаях, когда Х является результатом действия большого числа различных факторов и нельзя точно установить, какой из факторов действует на Х больше всех остальных.
Примерами случайных величин, описываемых нормальным законом, являются:
1) Отклонение действительных размеров деталей при их обработке на станке от номинальных размеров
2) Отклонение снаряда от цели при стрельбе из орудия
3) Дальность полета снаряда при стрельбе из орудия
Нормальный закон распределения – к нему стремятся все другие законы распределения при определенных условиях.
Пример: Найдем вероятность попадания случайных величин в заданный интервал, если случайные величины подчиняются нормальному закону распределения.
P(α < x< β) = 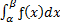 =
= 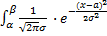 dx =
dx = 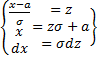 =
= 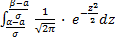 = Φ (
= Φ (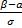 ) – Φ (
) – Φ (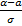 ), где Φ -функция Лапласса =
), где Φ -функция Лапласса = 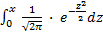 = Φ (
= Φ (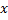 )
)
X1=z 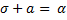 отсюда следует z=
отсюда следует z= 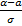 ; х2= z
; х2= z  отсюда следует z=
отсюда следует z=