
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление вероятности заданного отклонения
|
|
В некоторых случаях надо определять вероятность того, что отклонение нормального числа Х по абсолютной величине меньше заданного числа δ.
P(Ι x-aΙ < δ) = P(a-δ < x< a+δ) = Φ 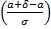 - Φ
- Φ 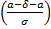 = Φ
= Φ 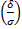 - Φ
- Φ  = 2Φ
= 2Φ 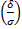
P(Ι x-aΙ < δ) = 2Φ 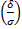 ; а = 0.
; а = 0.
Вероятность принять значение от δ до –δ больше у той величины, у которой наименьшее значение 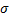 .
.
Правило трех сигм ( 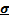 )
)
Преобразуем формулу, полученную в предыдущем случае.
P(Ι x – a Ι < δ) = 2Φ 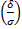
Пусть δ = 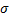 · t
· t
P(Ι x - a Ι < 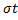 ) = 2Φ
) = 2Φ 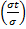
P(Ι x – a Ι < 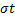 ) = 2Φ
) = 2Φ 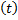
Если t = 3
P(Ι x – a Ι < 3 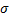 ) = 2Φ
) = 2Φ 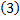
Но Φ 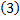 = 0, 49865
= 0, 49865
P(Ι x – a Ι < 3 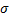 ) = 0, 49865 · 2 = 0, 9973
) = 0, 49865 · 2 = 0, 9973
Вероятность того, что отклонение будет меньше устроенного среднего квадратичного отклонения = 9973
Отсюда следует, что событие состоящее в том, что абсолютное отклонение превысит тройное среднее квадратичное отклонение практически невозможно, т.к. = 0, 0027.
Отсюда правило трех сигм: Если случайная величинараспределена по нормальному закону, то абсолютная величина ее отклонения от математического ожидания не будет превосходить утроенное среднее квадратичное отклонение.
На практике применяется так:
Если имеется случайная величина с неизвестным законом распределения и для нее выполняется условие, указанное в правиле з-х сигм, то эта случайная величина может считаться распределенной по нормальному закону.