Определение первообразной

Методические указания к проведению лекционного занятия

Тема № 4.1. Первообразная и неопределённый интеграл

План:

1. Определение первообразной

2. Определение неопределенного интеграла

3. Таблица основных интегралов

4. Свойства неопределенного интеграла

Определение первообразной

Функция F (x) называется первообразной для функции f (x) на промежутке Х, если для всех x Î Х выполняется равенство

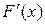= f (x).

Например, функция x ⁴/4 является первообразной для функции x ³, т.к.

.

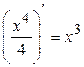Теорема 1. Если F (x) – первообразная для функции f (x) на промежутке Х, то F (x) + C, где C – произвольное число, тоже является первообразной для функции f (x) на Х.

Доказательство. По правилу дифференцирования суммы имеем:

(F (x)+ C) ¢ = F¢ (x)+ C¢ = f (x) + 0 = f (x),

т.е. по определению первообразной получим, что F (x)+ C - также первообразная для f (x), что и требовалось доказать.

Теорема 2. Если F (x) есть первообразная для функции f (x) на промежутке Х, а G (x) – другая первообразная для функции f (x) на Х, то G (x)= F (x)+ C, где C – произвольное число.

Доказательство. По правилу дифференцирования разности имеем:

(G (x)– F (x)) ¢ = G¢ (x) – F¢ (x) = f (x) – f (x) = 0.

Отсюда следует: G (x) – F (x) = C, где C ¾ число, т. е. G (x)= F (x) + C.