
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель кореляційно-регресивного аналізу
|
|
На аналітичному зображенні лінії регресії базується метод кореляційного регресійного аналізу (КРА). Лінія регресії описується з допомогою рівняння регресії такого виду:
Y=P(x), де Y – теоретичне значення результуючоъ ознаки “y”, що обчислюється за рівнянням регресії.
Таким чином, завдання регресії полягає в тому, щоб наявну залежність між ознаками y і x відобразити кількісно, тобто визначити наскільки в середньому зміниться значення результативної ознаки зі зміною на певну величину значення факторної ознаки.
Взалежності від конкретних умов і сум досліджуваних явищ при вивченні кореляційних зв’язків частіше інших використовуються такі функції
1) 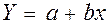 (лінійна)
(лінійна)
2) 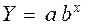 (степенева)
(степенева)
3) 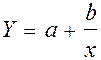 (гіпербола)
(гіпербола)
4) 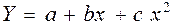 (парабола) і т.д.
(парабола) і т.д.
3а) Першим етапом КРА є відображення факторних ознак та вибір форми рівняння регресії. Фактори обираються на основі глибокого теоретичного аналізу суті явищ що вивчаються. Аналізуючи явища можна також вибрати і вид рівняння регресії. Проте більш надійним засобом, що дозволяє вибрати рівняння регресії є графічний, тобто побудова так званого кореляційного поля.
Після того, як вибрано рівняння регресії, що на думку дослідника може відобразити залежність ознаки y від ознаки x слід оцінити лінію регресії. Оцінити лінію регресії в КРА – це значить обчислити теоретичні значення результативної ознаки Y для кожного з значень факторної ознаки за даними рівняння.
Для цього необхідно перш за все обчислити параметри рівняння.
Уявимо собі, що залежність описується рівнянням прямої: 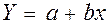 .
.
Параметри a і b обчислюються за способом найменших квадратів, тобто при щоб  . Цьому способу відповідає система таких двох нормальних рівнянь:
. Цьому способу відповідає система таких двох нормальних рівнянь:

Відшукавши параметри можна обчислити теоретичні рівні X.
Після оцінки лінії регресії слід оцінити тісноту зв’язку. Це завдання вірішується таким же чином, як і при дослідженні зв’язку на основі аналітичного групування. (універсальним) тісноти зв’язку в КРА є так званий коефіцієнт детермінації, обчислення якого базується на правилі складання дисперсій
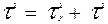 залишкова
залишкова
 – загальна дисперсія
– загальна дисперсія
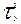 – факторна дисперсія, що характеризує систематичну варіацію
– факторна дисперсія, що характеризує систематичну варіацію
 залишкова – варіацію, обумовлену рештою факторів.
залишкова – варіацію, обумовлену рештою факторів.
Коефіцієнт детермінації обчислюється так
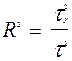
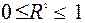
 – зв’язок між ознаками x і y відсутній.
– зв’язок між ознаками x і y відсутній.
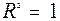 – функціональний зв’язок.
– функціональний зв’язок.
Часом використовується для оцінки тісноти зв’язку так званий індекс кореляції  . Коефіцієнт детермінації як показник тісноти зв’язку використовується при залежності (лінійна чи нелінійна). Дисперсії в КРА обчислюються за формулами:
. Коефіцієнт детермінації як показник тісноти зв’язку використовується при залежності (лінійна чи нелінійна). Дисперсії в КРА обчислюються за формулами:
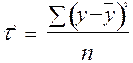
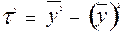
Ця дисперсія характеризує міру варіації ознаки y, обумовлену впливом всіх без вийнятку факторів
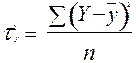
Ця дисперсія характеризує міру варіації ознаки y, обумовлену впливом саме ознаки x
 залишкова=
залишкова=  .
.
Характеризує міру варіації ознаки y, обумовлену впливом решти ознак, тобто за вийнятком впливу ознаки x.
При вивченні лінійної залежності в окремих випадках користуються таким показником тісноти зв’язку, як лінійний коефіціент кореляції r

Чим блищий цей показник до одиниці, тим тісніше вважається зв’язок.
Цей зв’язок находиться в межах:
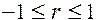
Якщо значення r від’ємне, це свідчить про те, що зв’язок між ознаками y і x обернений. При умові лінійного зв’язку |r|=R
Перевірка істотності зв‘язку в КРА аналогічна перевірці в МАГ, проте число ступенів свободив КРА залежить не від числа груп як в МАГ, а від числа параметрів обраного рівняння. В КРА m – число параметрів.
Для перевірки істотності 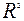 фактичне чи Fфактичне співставити з критичним (табличним) значеннями цих показників
фактичне чи Fфактичне співставити з критичним (табличним) значеннями цих показників
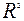 фактичне
фактичне 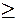
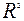 криитчне
криитчне
Fфактичне > F криитчне, то зв’язок визнається істотним.