
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Знакопеременные ряды
|
|
ГЛАВА 8. ЧИСЛОВЫЕ РЯДЫ
Основные понятия
Пусть 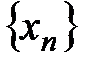 =
=  - числовая последовательность.
- числовая последовательность.
Определение 1. Выражение вида (формально составленная сумма)
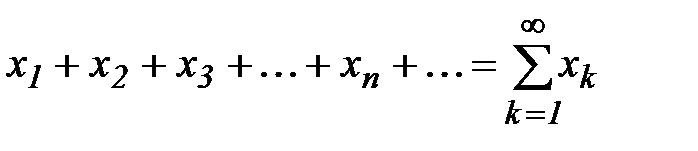 (1)
(1)
называется числовым рядом, а 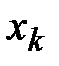 - его к -м членом.
- его к -м членом.
Другими словами, ряд есть бесконечная сумма членов некоторой числовой последовательности. Сумма первых n членов числовой последовательности 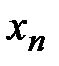 называется частичной суммой ряда и обозначается
называется частичной суммой ряда и обозначается 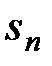 :
:
 .
.
Числовая последовательность 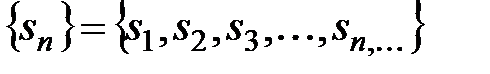 называется последовательностью частичных сумм.
называется последовательностью частичных сумм.
Определение 2. Числовой ряд называется сходящимся, если сходится последовательности его частичных сумм 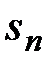 .
.
Предел последовательности 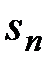 , равный
, равный 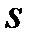 , называют суммой ряда:
, называют суммой ряда:
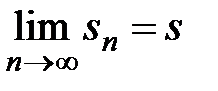 .
.
В этом случае пишут  . Если последовательность
. Если последовательность 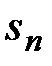 расходится, то говорят, что и числовой ряд расходится. Можно записать
расходится, то говорят, что и числовой ряд расходится. Можно записать
 .
.
Величина 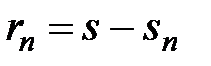 называется остатком ряда.
называется остатком ряда.
Замечание. По определению 2 сходимость ряда (1) равносильна сходимости числовой последовательности 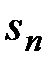 . Наоборот, если
. Наоборот, если 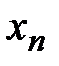 - некоторая числовая последовательность, то вопрос о ее сходимости равносилен сходимости ряда
- некоторая числовая последовательность, то вопрос о ее сходимости равносилен сходимости ряда 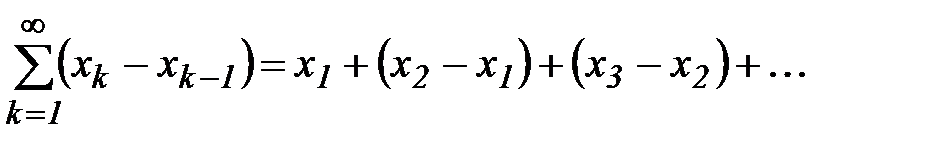 ,
, 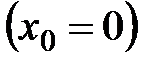 , для которого частичными суммами будут как раз члены последовательности
, для которого частичными суммами будут как раз члены последовательности 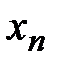 . Это иногда используют для доказательства сходимости рядов и последовательностей.
. Это иногда используют для доказательства сходимости рядов и последовательностей.
Таким образом, числовые ряды есть новая форма изучения числовых последовательностей.
Одна из главных задач теории числовых рядов состоит в изучении вопроса о сходимости и расходимости.
Пример 1. а) Исследовать сходимость ряда 
Рассмотрим последовательность частичных сумм:  ,
, 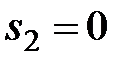 ,
, 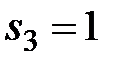 ,
, 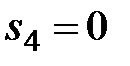 , ….,
, ….,  ,
, 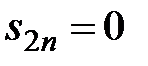 , … т.е.
, … т.е.  .
.
Эта последовательность не имеет предела, поэтому ряд расходится.
б) Исследовать сходимость ряда 
Составим последовательность частичных сумм 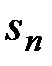 . Так как
. Так как
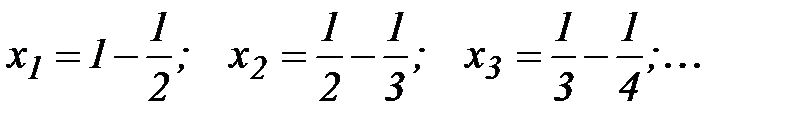
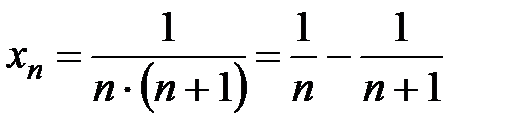 ,
,
то 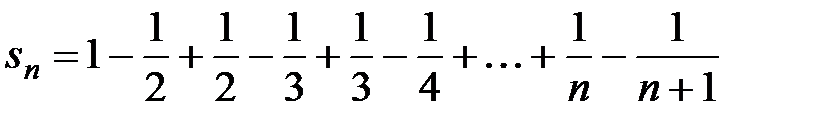
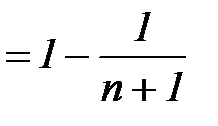 .
.
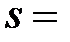
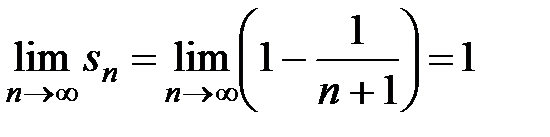 , откуда следует, что ряд сходится.
, откуда следует, что ряд сходится.
Аналогичным образом найти сумму ряда 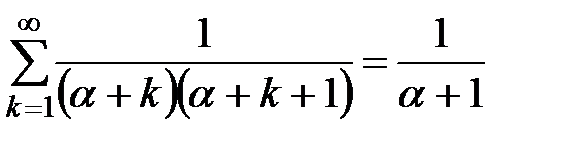 , где
, где 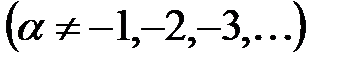
в) Исследовать сходимость ряда в зависимости от параметра q: 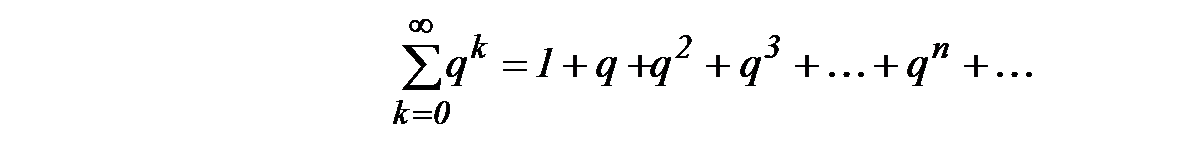
Частичной суммой ряда является сумма геометрической прогрессии:
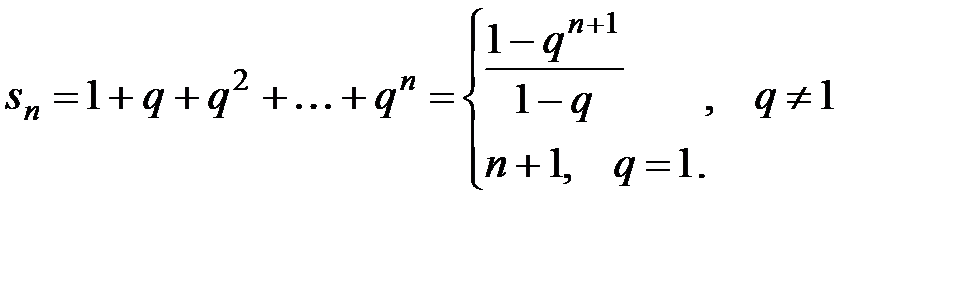 .
.
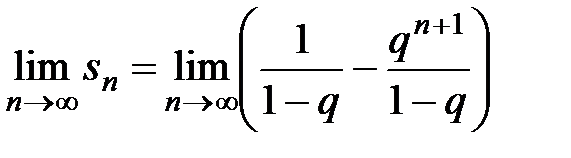 .
.
Если  ,
, 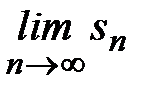 не существует и ряд расходится;
не существует и ряд расходится;
если 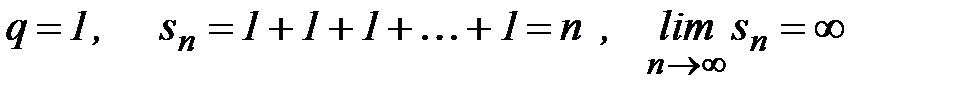 - ряд расходится;
- ряд расходится;
если 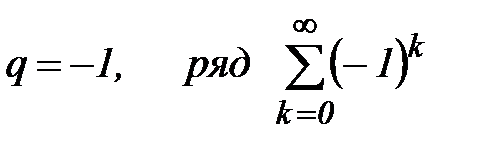 расходится (см. пример 1):
расходится (см. пример 1):
если 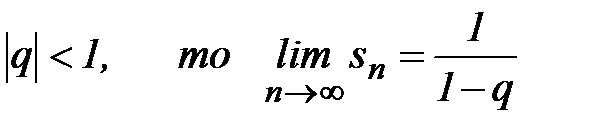 =
=  , т.к.
, т.к. 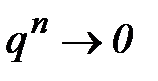 и ряд сходится.
и ряд сходится.
г) Показать, что ряд 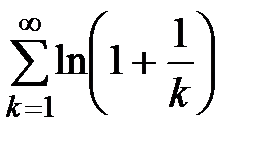 расходится.
расходится.
Так как частичную сумму  можно записать как
можно записать как  , то
, то 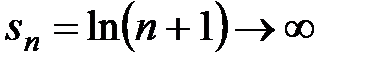 при
при  и ряд расходится.
и ряд расходится.
Пусть 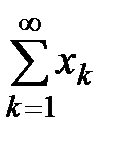 и
и 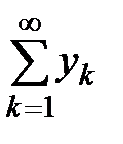 - два числовых ряда.
- два числовых ряда.
Определение 3. Суммой и разностью этих рядов, а также произведением ряда на число называют следующие ряды:

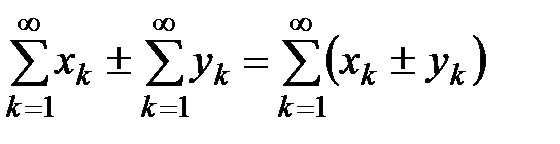 ;
; 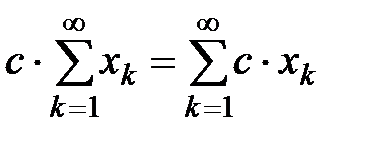 .
.
Теорема 1. Если ряды 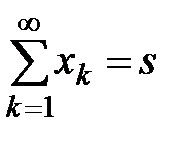 и
и 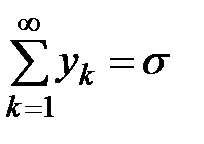 сходятся, то сходится их сумма, разность и произведение на число, причем
сходятся, то сходится их сумма, разность и произведение на число, причем  ;
; 
□ Пусть 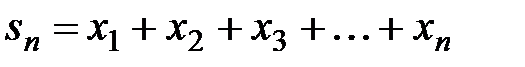 ,
, 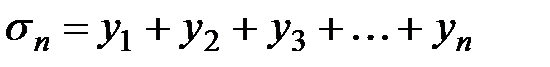 - частичные суммы заданных рядов, а
- частичные суммы заданных рядов, а 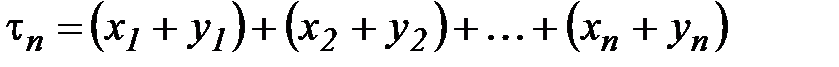 - частичная сумма ряда
- частичная сумма ряда 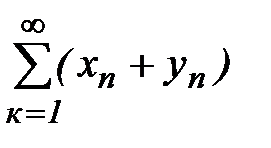 . Т.к.
. Т.к. 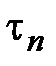 - конечная сумма, то слагаемые в ней можно переставлять, т.е.
- конечная сумма, то слагаемые в ней можно переставлять, т.е.
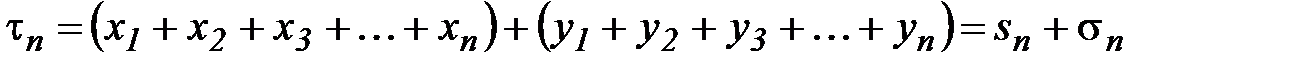 .
.
Откуда 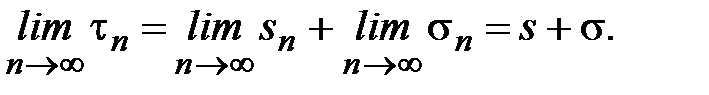 Аналогично доказывается для
Аналогично доказывается для 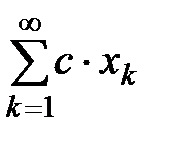 и
и 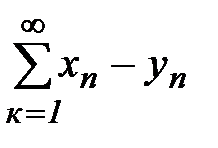 . ■
. ■
Замечание. Отбрасывание или добавление конечного числа слагаемых к членам ряда не влияет на его сходимость или расходимость, т.к. в этом случае его частичная сумма изменится на постоянное число.
Теорема 2. (Критерий Коши) Для сходимости ряда 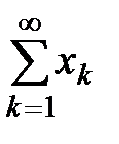 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  (2)
(2)
Очевидно, что неравенство (2) равносильно следующему:
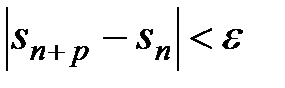 (3)
(3)
□ По определению сходимость ряда (1) равносильна сходимости последовательности 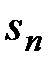 , поэтому условие сходимости ряда совпадает с условием сходимости числовой последовательности
, поэтому условие сходимости ряда совпадает с условием сходимости числовой последовательности 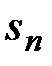 .
.
Необходимым и достаточным условием сходимости последовательности является критерий Коши: 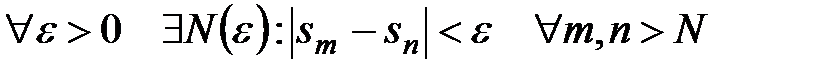 .
.
Обозначим 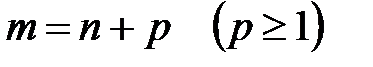 , тогда
, тогда  . ■
. ■
Следствие. (Необходимое условие сходимости ряда) Если ряд (1) сходится, то 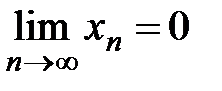
□ При 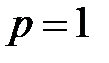 получим, согласно критерия Коши, что
получим, согласно критерия Коши, что 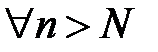
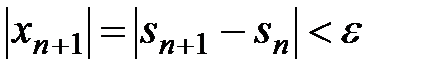 , т.е.
, т.е. 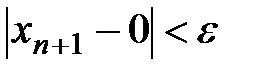 , т.е.
, т.е. 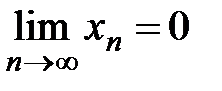 . ■
. ■
Отметим, что это условие необходимое, но не достаточное, т.е. если предел равен нулю, то ряд может сходиться, а может и расходиться.
Пример 2. Рассмотрим ряд 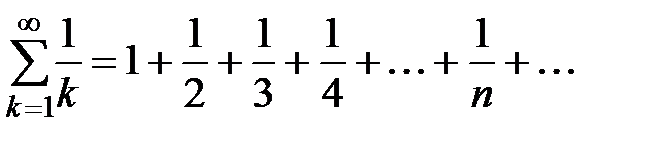 , который называется гармоническим рядом.
, который называется гармоническим рядом.
Очевидно, что 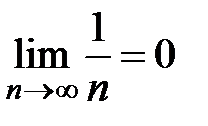 . Докажем, что ряд расходится. Воспользуемся критерием Коши. Возьмем
. Докажем, что ряд расходится. Воспользуемся критерием Коши. Возьмем 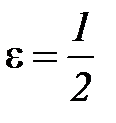 и
и  . Тогда
. Тогда
 .
.
Т.е. критерий Коши не выполняется и ряд расходится.
8.2. Признаки сходимости знакоположительных рядов
Определение 4. Числовой ряд
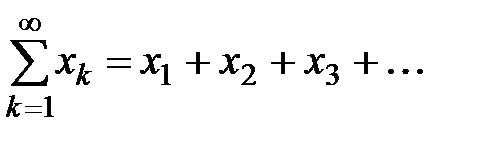 (4)
(4)
называется знакоположительным, если  .
.
Если, то ряд называется знакоотрицательным. Знакоположительные и знакоотрицательные ряды называются знакопостоянными. Для исследования сходимости знакопостоянных рядов достаточно изучать сходимость знакоположительных рядов.
Теорема 3. (основной признак) Для того, чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы его частичные суммы были ограничены сверху, т.е.
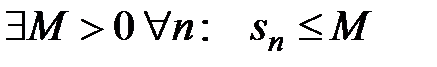 (5)
(5)
□ Необходимость. Пусть ряд сходится, тогда 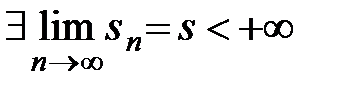 . Т.к.
. Т.к. 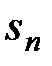 сходится, то она ограничена, следовательно, она ограничена и сверху.
сходится, то она ограничена, следовательно, она ограничена и сверху.
Достаточность. Пусть последовательность 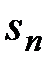 ограничена сверху. Но
ограничена сверху. Но 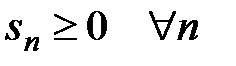 , т.е.
, т.е. 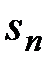 ограниченая и снизу, например нулём. Т.е.
ограниченая и снизу, например нулём. Т.е. 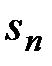 ограничена, причем очевидно, что
ограничена, причем очевидно, что
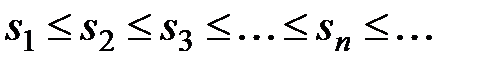 ,
,
т.е. она монотонная. Но всякая монотонная ограниченная последовательность имеет предел, т.е. 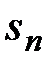 сходится, а, следовательно, ряд
сходится, а, следовательно, ряд  сходится.
сходится.
■
Теорема 4. (Признак разреженности)Пусть члены знакоположительного ряда монотонно убывают, т.е.  Тогда ряд
Тогда ряд 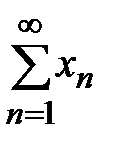 сходится тогда и только тогда, когда сходится ряд
сходится тогда и только тогда, когда сходится ряд 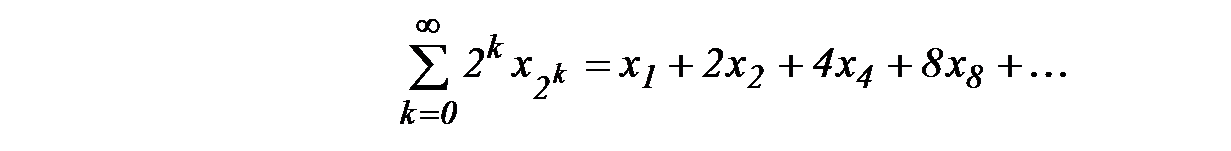 (6)
(6)
□ По основному признаку достаточно установить ограниченность частичных сумм. Обозначим
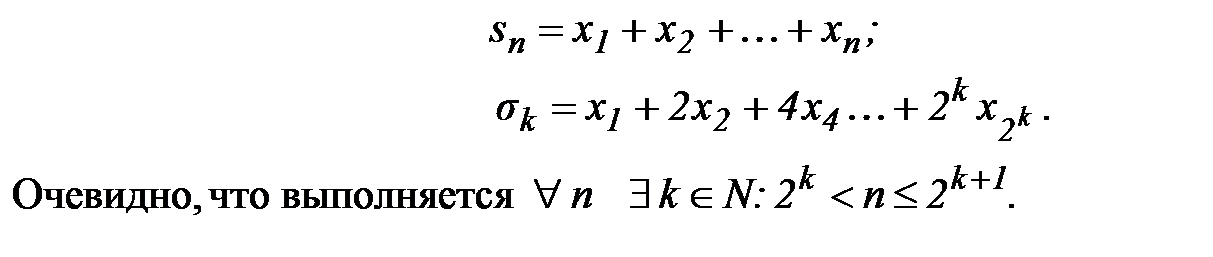
Тогда т.к. 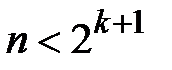 , то будем иметь
, то будем иметь
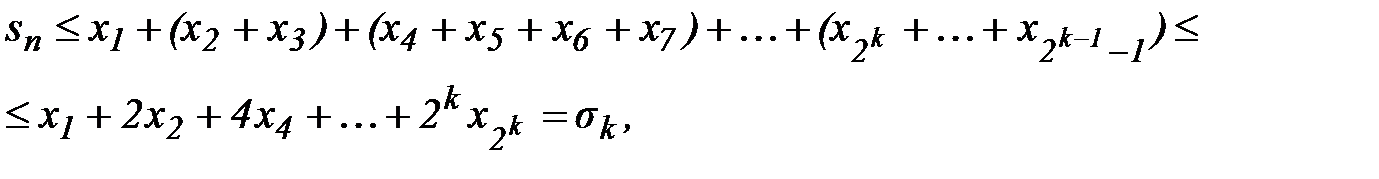
т. к. 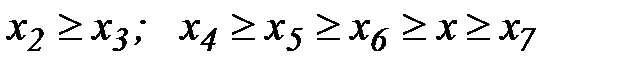 …. Таким образом
…. Таким образом  .
.
С другой стороны:
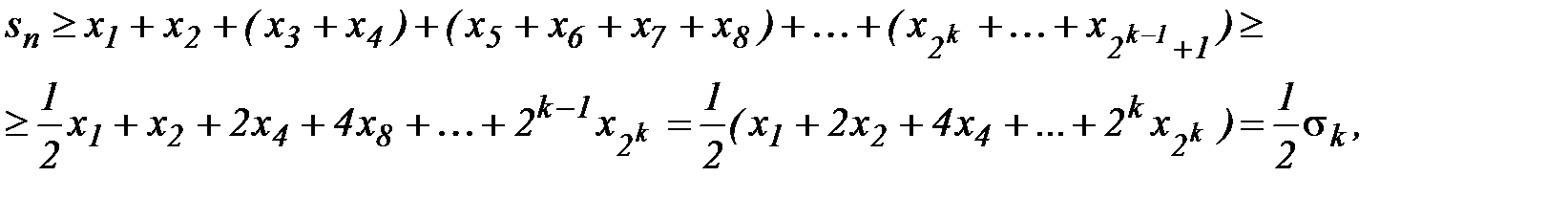 т.е.
т.е. 

Отсюда обе последовательности частичных сумм либо ограничены, либо неограниченны, отсюда по обе частичные суммы сходятся или расходятся одновременно, то и ряды сходятся или расходятся одновременно. ■
Пример 3. Ряд 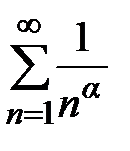 называется обобщенным гармоническим рядом. Исследовать его сходимость в зависимости от параметра α.
называется обобщенным гармоническим рядом. Исследовать его сходимость в зависимости от параметра α.
Если 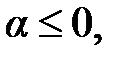 то частичные суммы неограниченны, т.е. ряд расходится.
то частичные суммы неограниченны, т.е. ряд расходится.
Если 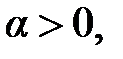 то по теореме 16 этот ряд сходится одновременно с рядом
то по теореме 16 этот ряд сходится одновременно с рядом
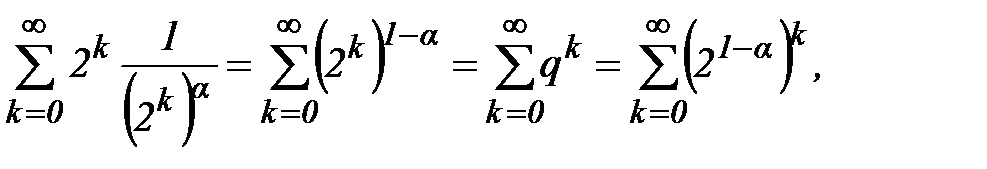 который сходится, если
который сходится, если 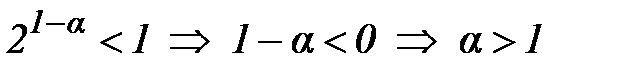 . При остальных – расходится.
. При остальных – расходится.
Теорема 5. (Признак сравнения) Пусть имеются два знакоположительных ряда:
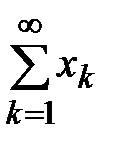 (7)
(7) 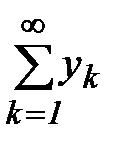 (8),
(8),
причем 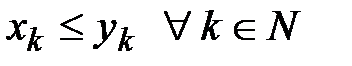 (9)
(9)
Тогда: а) если ряд (8) сходится, то сходится и ряд (7); б) если ряд (7) расходится, то расходится и ряд (8).
□ Обозначим частичные суммы рядов:
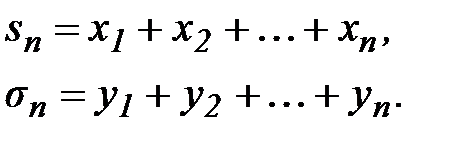
а) Если ряд (8) сходится, то его частичные суммы ограничены сверху, т.е. 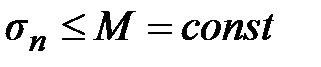 . Но из (9) следует, что
. Но из (9) следует, что 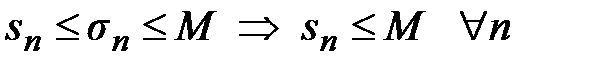 , т.е. частичные суммы ряда (7) также ограничены, тогда по основному признаку ряд (7) сходится;
, т.е. частичные суммы ряда (7) также ограничены, тогда по основному признаку ряд (7) сходится;
б) Докажем второе утверждение от противного. Пусть 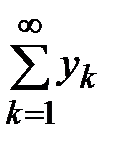 сходится, тогда по утверждению а) должен сходиться и ряд (7), но по условию он расходится. Противоречие, следовательно ряд (8) расходится. ■
сходится, тогда по утверждению а) должен сходиться и ряд (7), но по условию он расходится. Противоречие, следовательно ряд (8) расходится. ■
Ряд (8) для ряда (7) называют мажорантой и говорят, что ряд (8) мажорирует ряд (7).
Пример 4. Исследовать сходимость рядов:
а)  ; Ясно, что
; Ясно, что 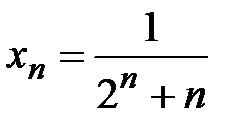 .
.
Рассмотрим ряд 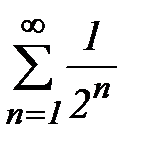 ,
, 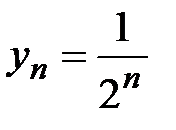 . Т.к.
. Т.к. 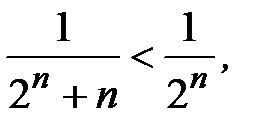 а ряд
а ряд  - сходится как геометрическая прогрессия, следовательно, исходный ряд сходится.
- сходится как геометрическая прогрессия, следовательно, исходный ряд сходится.
б) 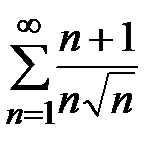 . Так как
. Так как 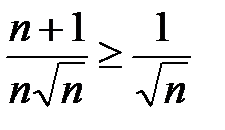 , а ряд
, а ряд 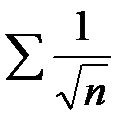 расходится, как обобщенный гармонический ряд, следовательно, и ряд
расходится, как обобщенный гармонический ряд, следовательно, и ряд 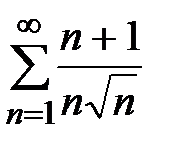 расходится.
расходится.
Теорема 6. (Предельный признак сравнения) Пусть даны два знакоположительных ряда (7) и (8). Тогда, если существует конечный и отличный от нуля предел
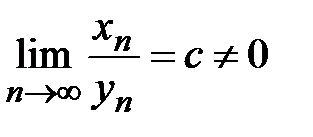 , (10)
, (10)
то эти ряды одновременно сходятся или расходятся.
 □ Пусть предел (10) существует. Очевидно, что с> 0 (
□ Пусть предел (10) существует. Очевидно, что с> 0 (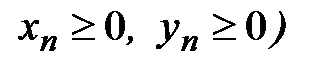 . Тогда
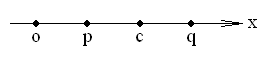
. Тогда 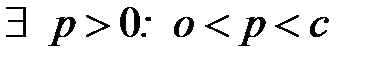 . Рассмотрим интервал (p, q) с центром в точке с. По определению предела, начиная с некоторого n, будет выполняться неравенство
. Рассмотрим интервал (p, q) с центром в точке с. По определению предела, начиная с некоторого n, будет выполняться неравенство
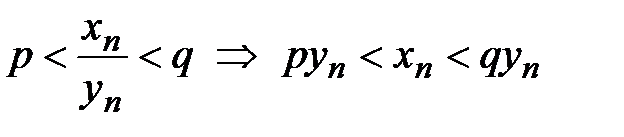 . (11)
. (11)
Пусть 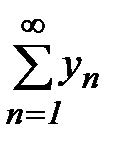 - сходится, тогда
- сходится, тогда 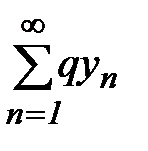 - тоже сходится, и по признаку сравнения из (11) ряд
- тоже сходится, и по признаку сравнения из (11) ряд 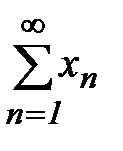 сходится.
сходится.
Если  - расходится, то
- расходится, то 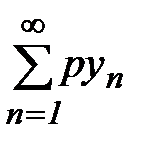 - тоже расходится и из (10) и теоремы ряд
- тоже расходится и из (10) и теоремы ряд  расходится. ■
расходится. ■
Следствие. Если с=0 и 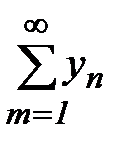 сходится, то сходится и ряд (7). Если с=+∞ и ряд
сходится, то сходится и ряд (7). Если с=+∞ и ряд 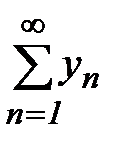 расходится, то ряд (7) расходится.
расходится, то ряд (7) расходится.
Пример 5. Исследовать сходимость ряда  .
.
1. Проверим необходимый признак:
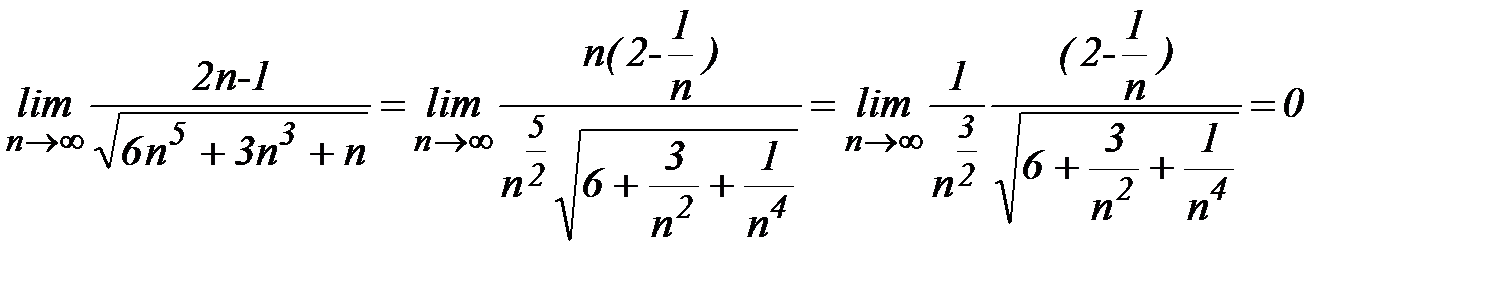
2. Используем достаточный признак сравнения в предельном виде
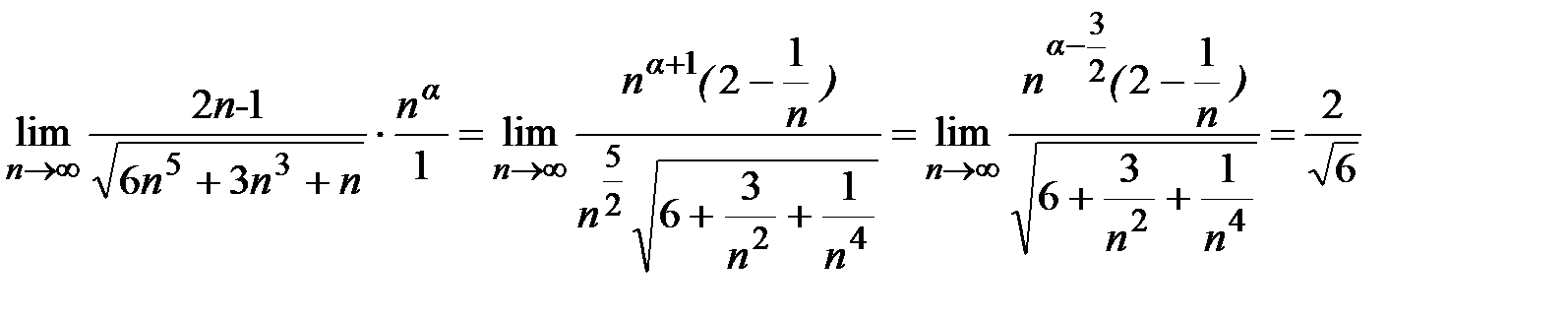
Этот предел будет конечен и равен 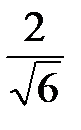 , когда
, когда 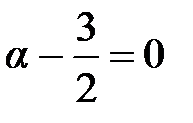 , т.е.
, т.е. 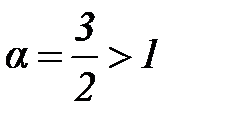 Т.к. обобщенный гармонический ряд сходится, то потеореме ряд сходится.
Т.к. обобщенный гармонический ряд сходится, то потеореме ряд сходится.
Теорема 7. (Признак Даламбера) (1717-1783 ) Если существует предел  , (12)
, (12)
то знакоположительный ряд 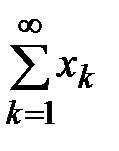 сходится при λ < 1 и расходится при λ > 1.
сходится при λ < 1 и расходится при λ > 1.
□ а) Пусть λ < 1. Тогда существует число q: λ < q< 1. Рассмотрим интервал (p, q) с центром в точке λ, т.е. (p, q)=Oε (λ). Следовательно, по определению предела 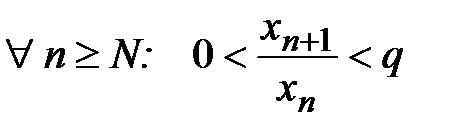 или
или 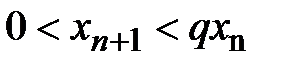 . Но тогда
. Но тогда
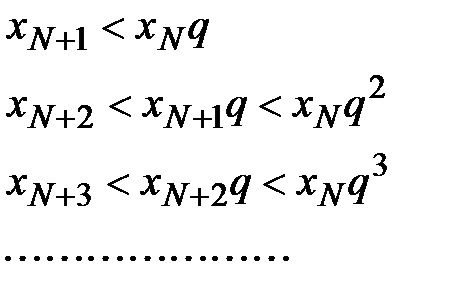
Т.е. члены ряда
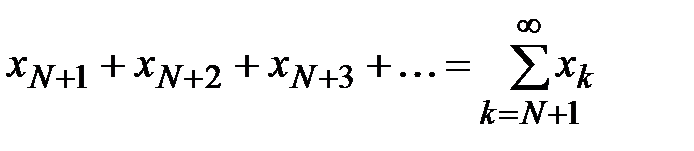 (13) не превосходят членов ряда
(13) не превосходят членов ряда
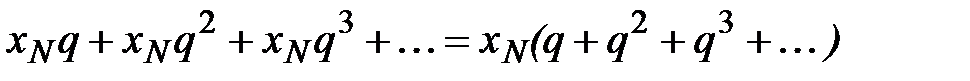 (14)
(14)
Но ряд (14) сходится как геометрическая прогрессия с q< 1. Тогда сходится и ряд (1) по признаку сравнения, а следовательно и ряд 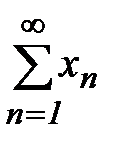 , т.к. к нему прибавлено конечное число слагаемых
, т.к. к нему прибавлено конечное число слагаемых 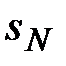 .
.
б) Пусть λ > 1, 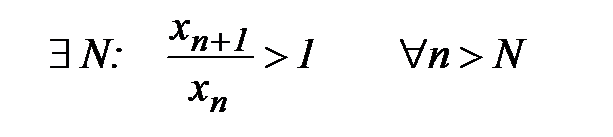 . Поскольку
. Поскольку  то общий член не стремится к нулю при n→ ∞. Следовательно, ряд расходится по необходимому признаку. ■
то общий член не стремится к нулю при n→ ∞. Следовательно, ряд расходится по необходимому признаку. ■
Пример 6. Исследовать сходимость ряда  .
.
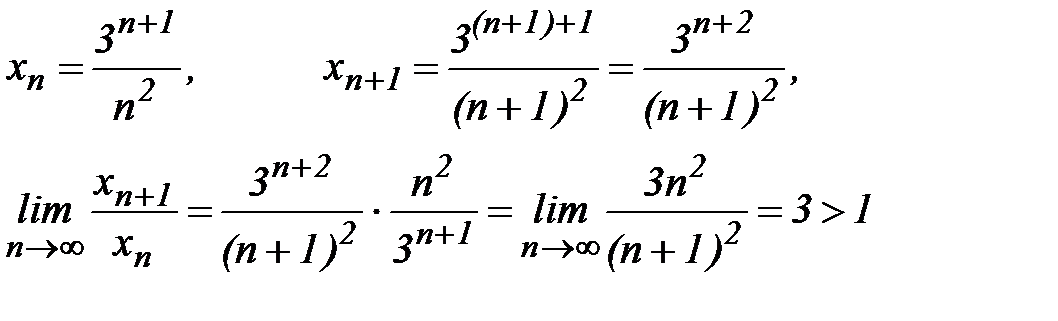
Согласно теоремы, ряд расходится.
Замечание. Если 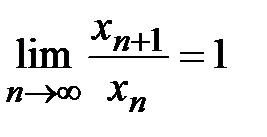 , то ряд может сходиться, а может и расходиться.
, то ряд может сходиться, а может и расходиться.
Теорема 8. ( Признак Коши) (1789-1857)Если существует конечный предел
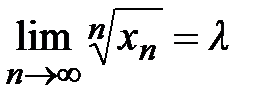 , (15)
, (15)
то в случае 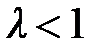 знакоположительный ряд
знакоположительный ряд 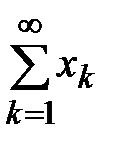 сходится, а при
сходится, а при 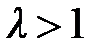 расходится.
расходится.
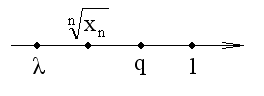 □ а) Пусть
□ а) Пусть  . Тогда
. Тогда  . Из определения предела следует, что, начиная с некоторого N, будет выполняться неравенство:
. Из определения предела следует, что, начиная с некоторого N, будет выполняться неравенство:
 .
.
Таким образом, при 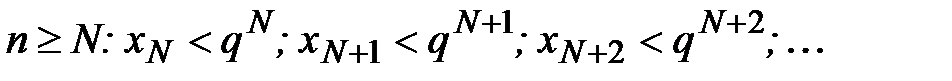 Т.е. члены ряда
Т.е. члены ряда  не превосходят членов ряда
не превосходят членов ряда  . Но последний ряд сходится как геометрическая прогрессия при q< 1, тогда по признаку сравнения сходится и ряд
. Но последний ряд сходится как геометрическая прогрессия при q< 1, тогда по признаку сравнения сходится и ряд 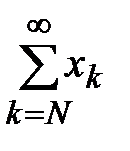 . Но тогда сходится и ряд
. Но тогда сходится и ряд  , т.к.
, т.к. 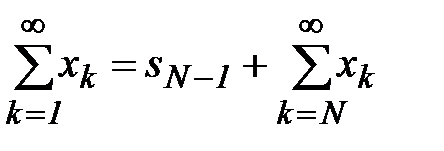 . Она образуется из сходимости ряда добавлением конечного числа
. Она образуется из сходимости ряда добавлением конечного числа 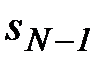 .
.
б) Пусть 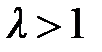 , тогда
, тогда
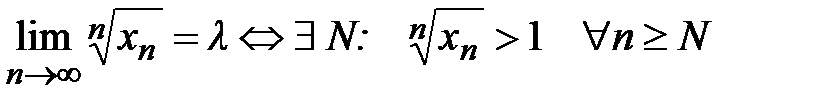 , т.е.
, т.е. 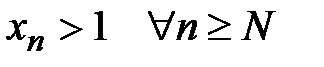 .
.
Следовательно,  не стремится к нулю и по необходимому признаку ряд расходится. ■
не стремится к нулю и по необходимому признаку ряд расходится. ■
Пример 7. Исследовать сходимость ряда 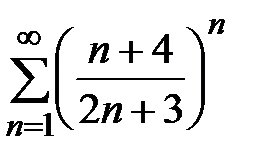 .
.
Замечание. При λ =1 ряд может сходиться, а может расходиться. Признак
В заключение, остановимся здесь на определении числа е, которое используется как основание для натуральных логарифмов 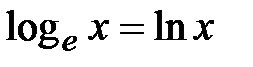 . Это можно сделать двумя способами. Во-первых, рассмотрим ряд
. Это можно сделать двумя способами. Во-первых, рассмотрим ряд
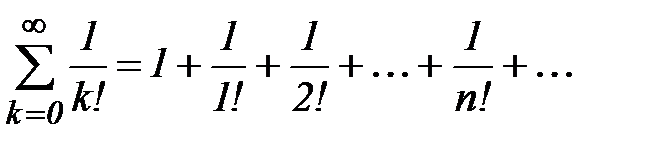 (16)
(16)
Покажем, что он сходится. При 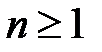 очевидно неравенство
очевидно неравенство 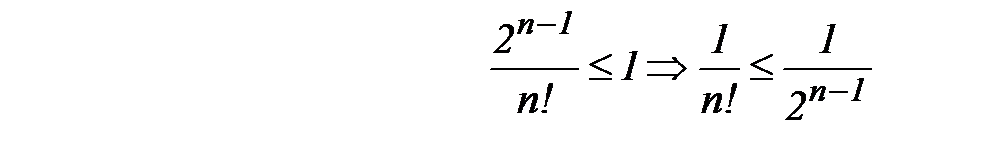 .
.
Ряд 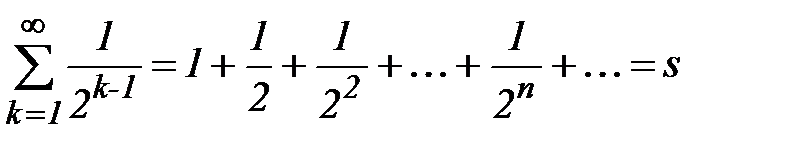 есть сумма бесконечно убывающей прогрессии, он сходится и его сумма
есть сумма бесконечно убывающей прогрессии, он сходится и его сумма
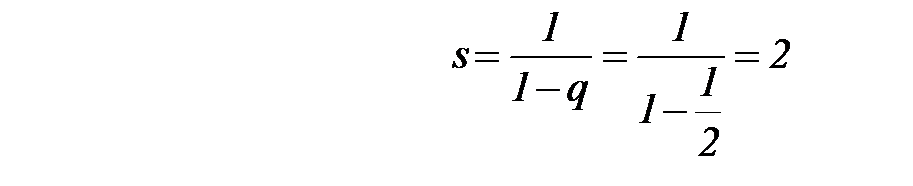 .
.
Тогда по признаку сравнения ряд (14) тоже сходится. Сумма этого ряда обозначается через е:

Очевидны следующие неравенства:
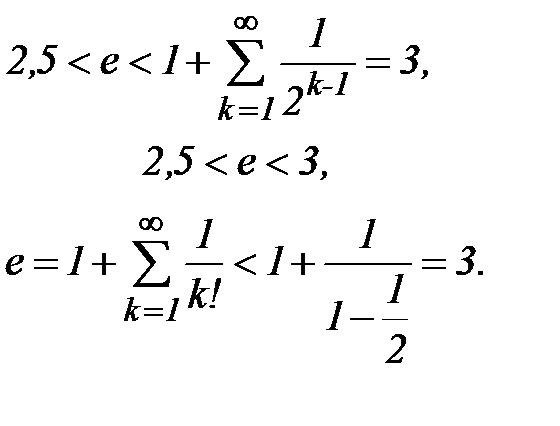
Оценим погрешность, с которой частичная сумма 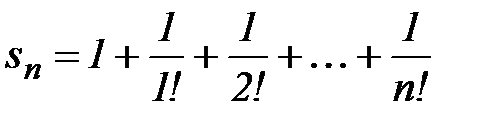 приближает число е. Рассмотрим разность
приближает число е. Рассмотрим разность 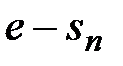

Таким образом, 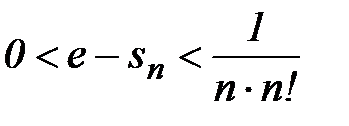 . Так, если n =6, n! =720, n! n =4320
. Так, если n =6, n! =720, n! n =4320 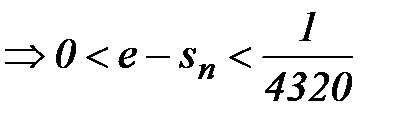 .
.
Число е с пятью знаками е ≈ 2, 71828. Причем е – иррациональное число.
Теперь покажем, что е есть предел последовательности 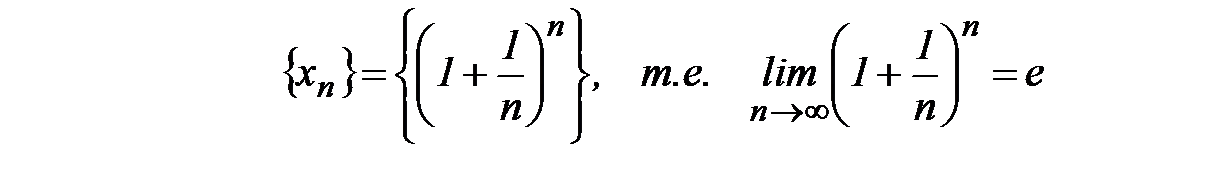 .
.
Воспользуемся биномом Ньютона:

При а=1, b=1/n получим:
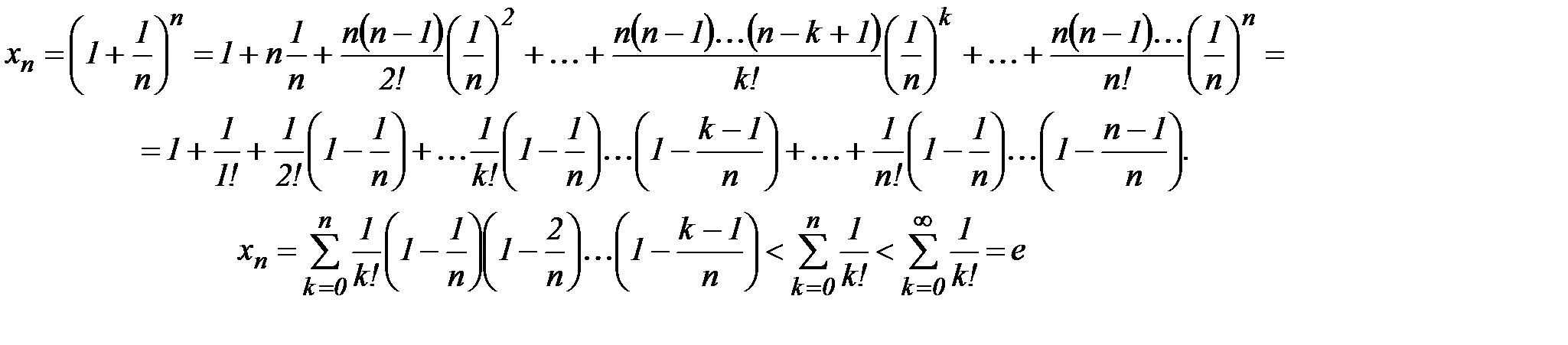
Тогда, очевидно неравенство:
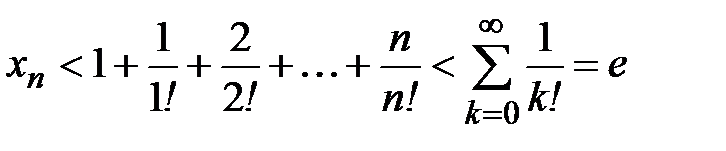
Таким образом, последовательность 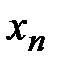 возрастает и ограничена сверху, следовательно, она сходится. Найдем ее предел.
возрастает и ограничена сверху, следовательно, она сходится. Найдем ее предел.
Фиксируем некоторое натуральное число m и построим последовательность
 .
.
Ясно, что при n> m: 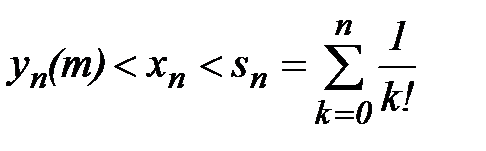 . Перейдем в этих неравенствах к пределу при n→ ∞:
. Перейдем в этих неравенствах к пределу при n→ ∞:
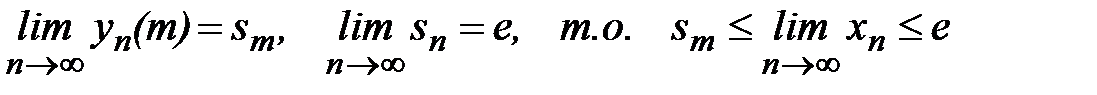 /
/
Переходя здесь к пределу при m→ ∞, получим:
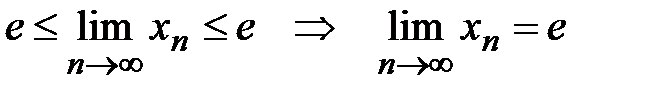 .
.
Знакопеременные ряды
Определение 5. Числовой ряд 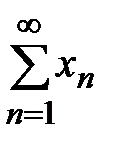 называется знакопеременным, если его члены
называется знакопеременным, если его члены  могут иметь как положительные, так и отрицательные знаки. Например,
могут иметь как положительные, так и отрицательные знаки. Например, 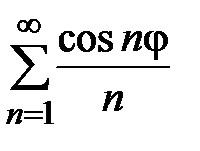 .
.
Теорема 9. (Достаточный признак сходимости)Если сходится ряд 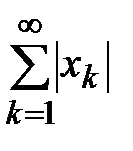 , то сходится и ряд
, то сходится и ряд 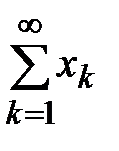 .
.
□ По критерию Коши, из сходимости 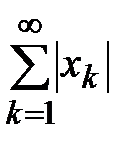 следует:
следует:
 , но справедливо неравенство
, но справедливо неравенство
 , т.е. выполняется критерий Коши для ряда
, т.е. выполняется критерий Коши для ряда 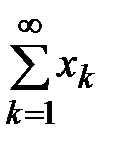 и он сходится. ■
и он сходится. ■
Пример 8. Знакопеременный ряд 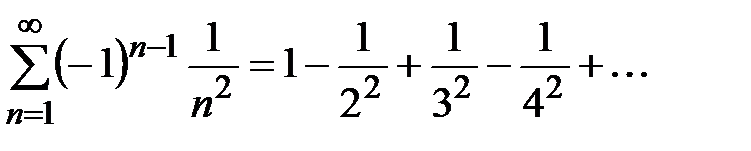 сходится, т.к. сходится обобщенный гармонический ряд с показателем равным двум.
сходится, т.к. сходится обобщенный гармонический ряд с показателем равным двум.
Определение 6. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов.
Из теоремы 9 ясно, что всякий абсолютно сходящийся ряд является просто сходящимся.
Определение 7. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример 9. Знакопеременный ряд 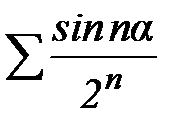 сходится абсолютно, т.к.
сходится абсолютно, т.к. 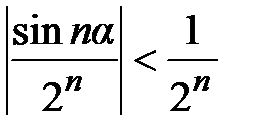 , а ряд
, а ряд 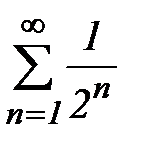 сходится.
сходится.
Среди знакопеременных рядов очень важное место занимают знакочередующиеся ряды, т.е. ряды вида:
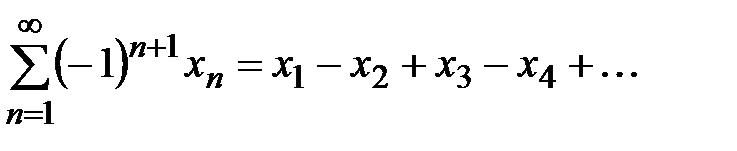 , (17)
, (17)
где 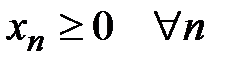 .
.
Такой ряд иногда называют рядом Лейбница. Для этих рядов справедлив достаточный признак.
Теорема 10. (Признак Лейбница)Пусть члены знакочередующегося ряда (17) монотонно убывают, т.е. 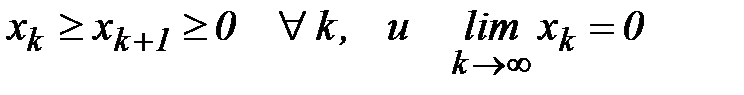 , тогда ряд сходится.
, тогда ряд сходится.
□ Обозначим через 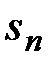 последовательность частичных сумм. Рассмотрим две ее подпоследовательности
последовательность частичных сумм. Рассмотрим две ее подпоследовательности 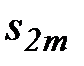 и
и 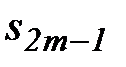 , m =1, 2, 3,...
, m =1, 2, 3,...
Последовательность 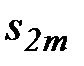 не убывает, т.к.
не убывает, т.к. 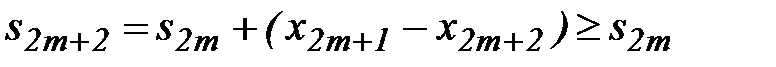 , т.к.
, т.к. 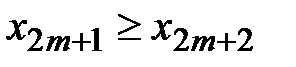 .
.
Последовательность 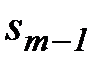 не возрастает, т.к.
не возрастает, т.к. 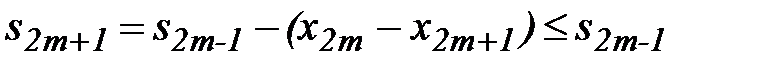 .
.
Последовательность 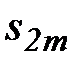 ограничена сверху. Действительно,
ограничена сверху. Действительно, 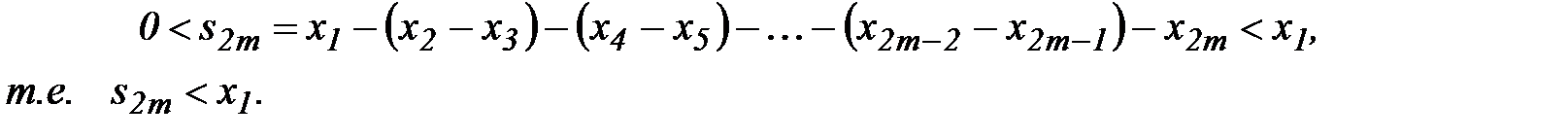 Т.е. подпоследовательность
Т.е. подпоследовательность 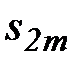 монотонная (не убывает) и ограничена сверху, следовательно, она имеет предел (конечный). Обозначим
монотонная (не убывает) и ограничена сверху, следовательно, она имеет предел (конечный). Обозначим
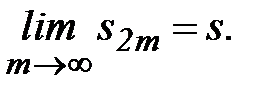
Но 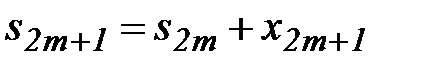 , тогда
, тогда 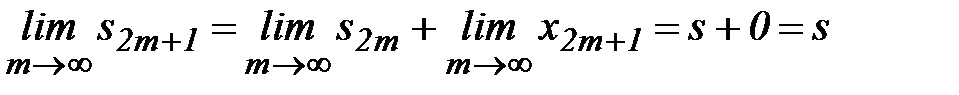 .
.
Следовательно, четные и нечетные суммы имеют один предел s. Тогда
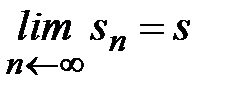 и ряд по определению сходится. ■
и ряд по определению сходится. ■
Следствие. Абсолютная погрешность при замене суммы знакочередующегося ряда его частичной суммой не превосходит первого отброшенного члена ряда, т.е. 
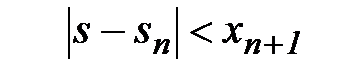
□ Т.к.  не возрастают и стремятся к s, а
не возрастают и стремятся к s, а 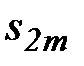 - не убывают и стремятся к s, то
- не убывают и стремятся к s, то 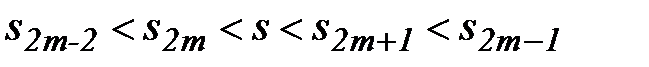 .Тогда
.Тогда
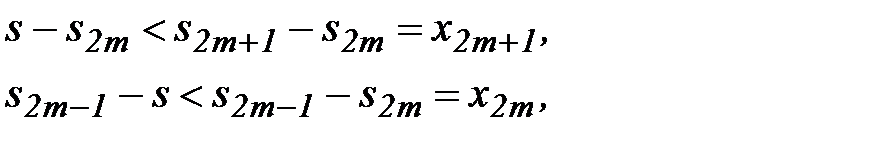
то есть
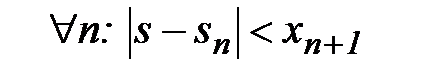 ■
■
Замечание. Теорема остается верной, если условие 
 выполняется, начиная с некоторого N.
выполняется, начиная с некоторого N.
Следствие играет большую роль в практических вычислениях с помощью рядов.
Пример10. Вычислить с точностью δ =0, 001 сумму ряда

 .
.
Так как 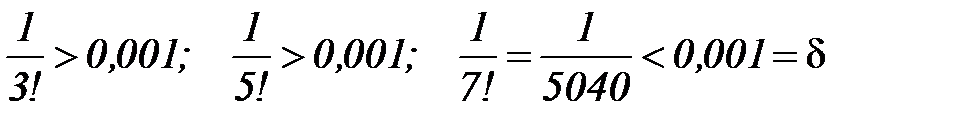 , то сумма будет приближенно равна
, то сумма будет приближенно равна 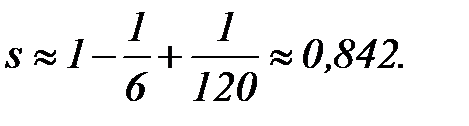
Теперь будем рассматривать произвольные знакопеременные ряды.
Теорема 11. (Признак Дирихле) Пусть дан 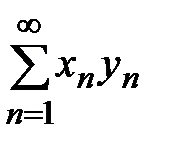 , такой, что последовательность
, такой, что последовательность 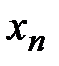 монотонно стремится к 0, а последовательность частичных сумм ряда
монотонно стремится к 0, а последовательность частичных сумм ряда 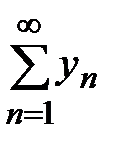 ограничена, тогда ряд
ограничена, тогда ряд 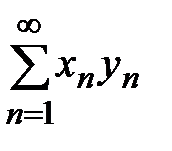 сходится.
сходится.
□ Вначале отметим, что имеет место неравенство Абеля при условиях данной теоремы
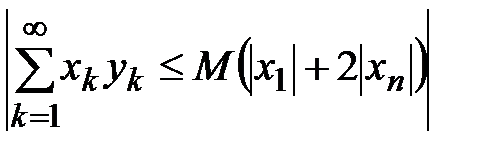 , (18)
, (18)
где М константа, ограничивающая последовательность частичных сумм 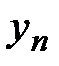 , т.е.
, т.е. 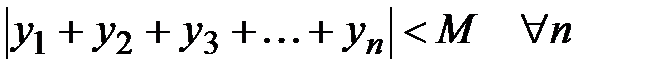 , т.е.
, т.е. 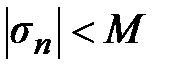
Перейдем к доказательству. В силу ограниченности последовательности 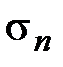 имеем
имеем
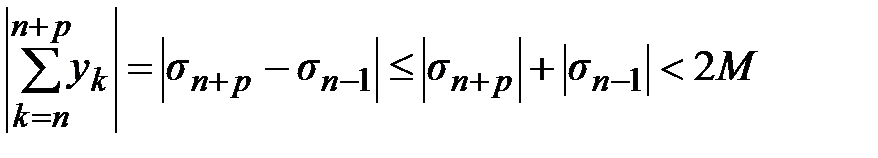
Проверим критерий Коши. Возьмем произвольное число ε > 0. Т.к.
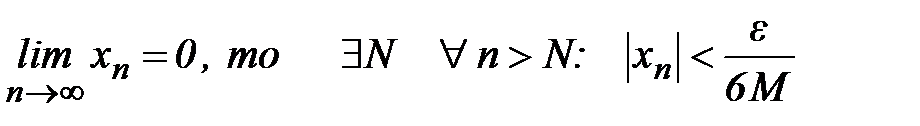 .
.
Теперь применим неравенство Абеля к сумме 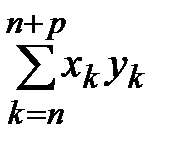 , где n> N
, где n> N

 , т.е. для ряда
, т.е. для ряда 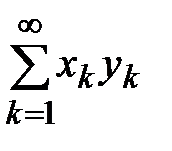 выполняется признак Коши, а, следовательно, он сходится. ■
выполняется признак Коши, а, следовательно, он сходится. ■
Пример 11. Исследовать сходимость ряда  .
.
Пусть α ≠ 2π m 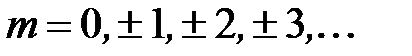 Тогда
Тогда

Тогда 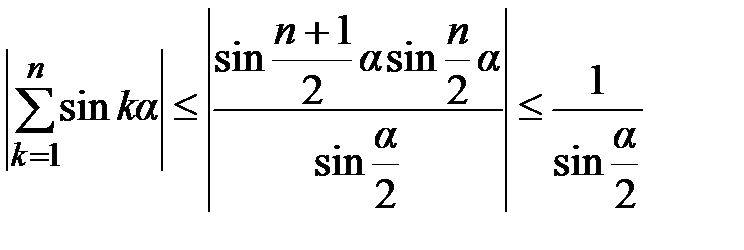
Если α =2π m, то все слагаемые равны нулю и сумма равна нулю. Т.о. 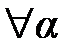 частичные суммы ограничены. Последовательность
частичные суммы ограничены. Последовательность  монотонно убывает и
монотонно убывает и 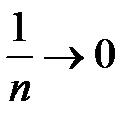 , следовательно, по признаку Дирихле ряд сходится.
, следовательно, по признаку Дирихле ряд сходится.
Замечание. Очевидно, признак Лейбница есть частный случай признака Дирихле при 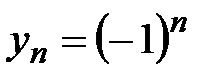 .
.
Теорема 12. (Признак Абеля) Если последовательность 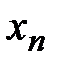 монотонна и ограничена, а ряд
монотонна и ограничена, а ряд 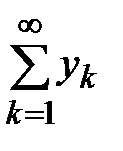 сходится, то сходится и ряд
сходится, то сходится и ряд 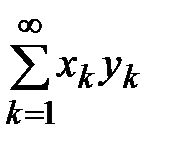 .
.
□ В силу ограниченности последовательности  и сходимости ряда
и сходимости ряда 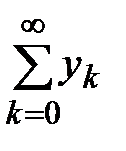 следует по критерию Коши
следует по критерию Коши
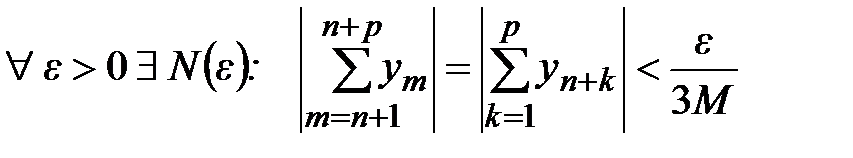
Тогда 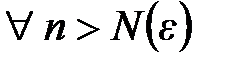 и всех целых
и всех целых 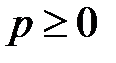 используя неравенство Абеля (18) имеем
используя неравенство Абеля (18) имеем

По критерию Коши ряд сходится. □
Пример 12. Исследовать сходимость ряда 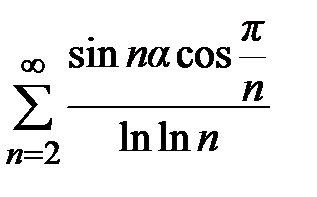 .
.
Ряд  сходится по признаку Дирихле, т.к. последовательность частичных сумм ряда
сходится по признаку Дирихле, т.к. последовательность частичных сумм ряда  ограничена, а
ограничена, а 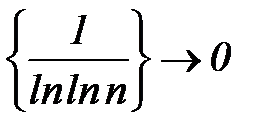 монотонно. Последовательность
монотонно. Последовательность 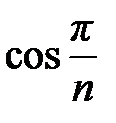 монотонна. Отсюда следует, что ряд сходится.
монотонна. Отсюда следует, что ряд сходится.
Следующие две теоремы показывают существенное различие между абсолютно и условно сходящимися рядами.
Теорема 13. (Риман)Если ряд знакопеременный ряд 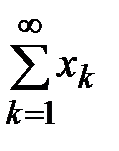 сходится условно и s произвольное вещественное число, то можно так переставить члены этого ряда, что полученный ряд будет иметь сумму равную s. (Без доказательства)
сходится условно и s произвольное вещественное число, то можно так переставить члены этого ряда, что полученный ряд будет иметь сумму равную s. (Без доказательства)
Пример 13. Ряд 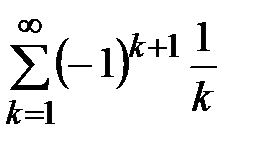 сходится условно. Пусть его сумма s. Сгруппируем слагаемые так: один положительный, затем два отрицательных, один положительный, затем два отрицательных и т.д., и найдем сумму
сходится условно. Пусть его сумма s. Сгруппируем слагаемые так: один положительный, затем два отрицательных, один положительный, затем два отрицательных и т.д., и найдем сумму
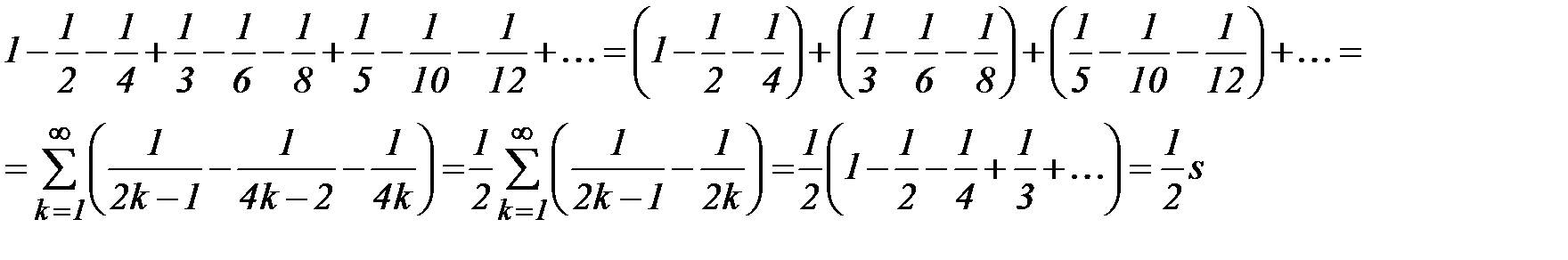
т.е. сумма изменилась, следовательно, переставлять слагаемые в условно сходящемся ряде нельзя.
Теорема 14. Если знакопеременный числовой ряд сходится абсолютно, то новый ряд, полученный перестановкой его членов, также сходится абсолютно и имеет ту же сумму. (Без доказательства)
1 2.7.Контрольные вопросы
26. Какое выражение называется числовым рядом? Что называется общим членом ряда?
27. Как определяется 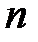 -я частичная сумма ряда?
-я частичная сумма ряда?
28. Что называется суммой ряда? Какие ряды называются сходящимися и расходящимися?
29. При каких условиях ряд бесконечной геометрической прогрессии сходится, а при каких расходится?
30. Сформулируйте основные свойства сходящихся рядов.
31. В чем состоит необходимый признак сходимости и необходимый признак расходимости ряда?
32. Сформулируйте основные достаточные признаки сходимости знакоположительных рядов: признак сравнения, признак Даламбера, радикальный признак Коши и признак разреженности.
33. Укажите условия сходимости и расходимости обобщенного гармонического ряда.
34. Какой ряд называется знакочередующимся? Сформулируйте признак Лейбница.
35. Какой ряд называется знакопеременным? Сформулируйте достаточный признак сходимости знакопеременного ряда.
36. В чем состоит отличие абсолютной и условной сходимости знакопеременного ряда?
37. Сформулируйте основные свойства знакопеременных рядов.