
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Отсюда получаем, что , следовательно, ряд
|
|
.
Пример 19. Рассмотрим ряд 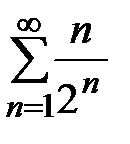 . Чтобы решить вопрос о сходимости последовательности
. Чтобы решить вопрос о сходимости последовательности 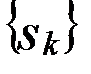 :
:  , преобразуем выражение
, преобразуем выражение  следующим образом:
следующим образом:
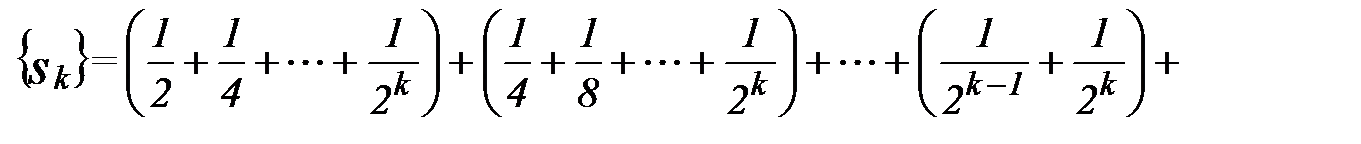
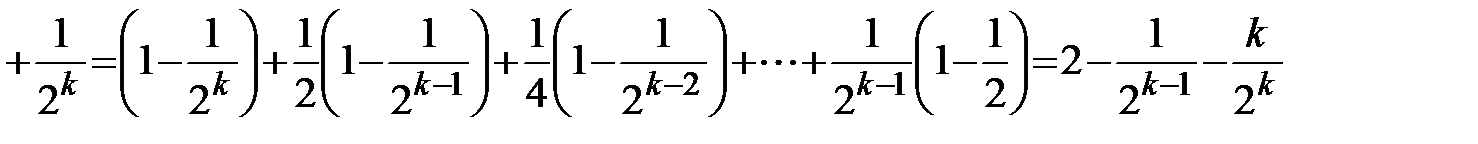 .
.
Отсюда получаем, что 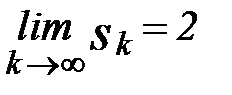 , следовательно, ряд
, следовательно, ряд  сходится и сумма его равна 2.
сходится и сумма его равна 2.
Пример 11. Рассмотрим ряд 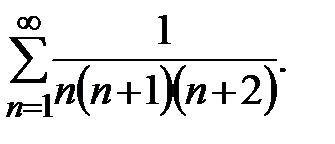 Для упрощения частичных сумм
Для упрощения частичных сумм

преобразуем выражение для члена ряда  , разложив его на простейшие дроби:
, разложив его на простейшие дроби:
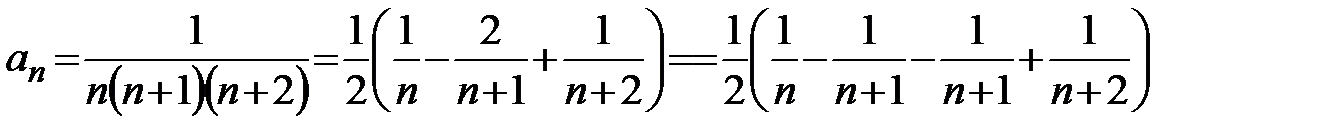 .
.
Отсюда получаем, что

 .
.
Следовательно, 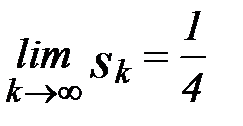 , т.е. ряд
, т.е. ряд 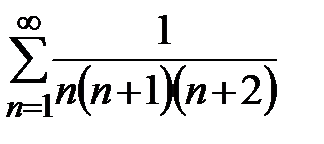 сходится и сумма его равна
сходится и сумма его равна  .
.
Пример 12. Рассмотрим ряд  . Так как
. Так как 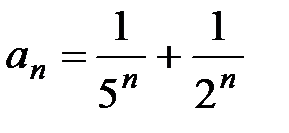 и каждый из рядов
и каждый из рядов 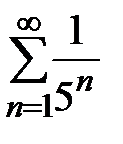 и
и 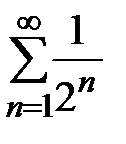 сходится, то и ряд
сходится, то и ряд 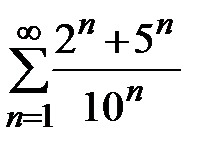 сходится.
сходится.
Пример 13. Рассмотрим ряд  . Так как
. Так как 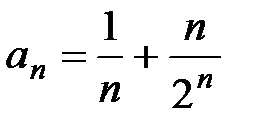 , ряд
, ряд  сходится (см. пример 1), а ряд
сходится (см. пример 1), а ряд  расходится, то ряд
расходится, то ряд 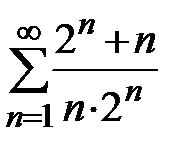 расходится.
расходится.
Пример 14. Рассмотрим ряд 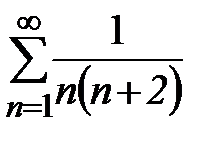 . Так как
. Так как  , то
, то

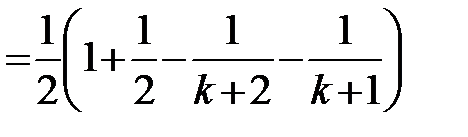 ,
,
следовательно 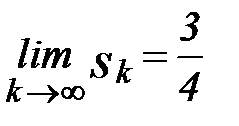 , т.е. ряд
, т.е. ряд 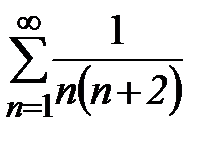 сходится и его сумма равна
сходится и его сумма равна 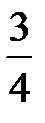 . В то же время, каждый из рядов
. В то же время, каждый из рядов 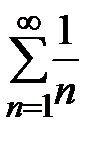 и
и  расходится.
расходится.
Пример 15. Рассмотрим ряд 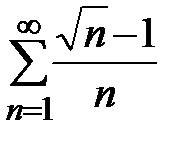 . Так как
. Так как  для
для  , то
, то 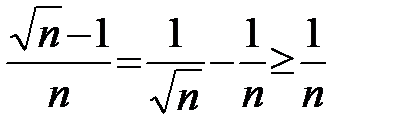 для
для 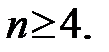 Пользуясь этими равенствами, получаем, что для любых натуральных
Пользуясь этими равенствами, получаем, что для любых натуральных  и
и 
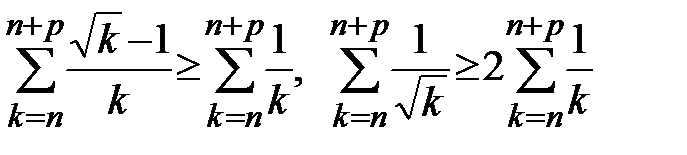 .
.
Пользуясь критерием Коши и расходимостью гармонического ряда, отсюда получаем, что ряды 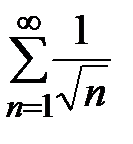 и
и 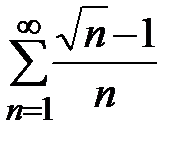 расходятся. Итак, расходятся все три ряда
расходятся. Итак, расходятся все три ряда  ,
, 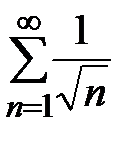 и
и  .
.
Пример 16. Рассмотрим ряд  . Для членов этого ряда имеем:
. Для членов этого ряда имеем:
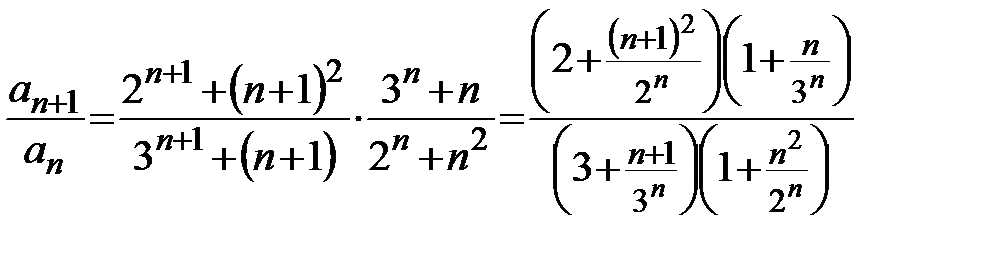 ,
,
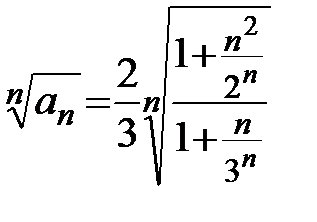 ,
,
откуда легко получаются оба равенства 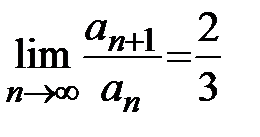 и
и  .
.
Итак, данный ряд сходится как по признаку Даламбера, так и признаку Коши.
Пример 17. Рассмотрим ряд 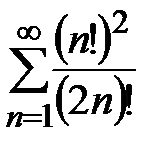 . Для этого ряда исследование сходимости ряда применим признак Даламбера:
. Для этого ряда исследование сходимости ряда применим признак Даламбера:
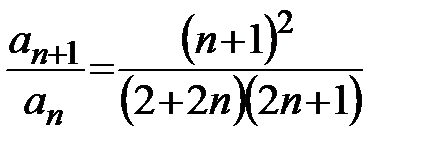 .
.
Так как 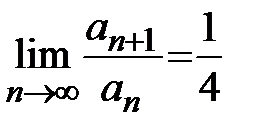 < 1, то в силу признака Даламбера данный ряд сходится.
< 1, то в силу признака Даламбера данный ряд сходится.
Пример 18. Рассмотрим ряд  . Поскольку члены ряда аналитически записаны в виде степени с переменным показателем, то следует ожидать, что исследование последовательности
. Поскольку члены ряда аналитически записаны в виде степени с переменным показателем, то следует ожидать, что исследование последовательности  будет проще, чем последовательности
будет проще, чем последовательности 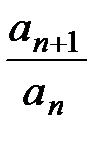 . Действительно, вычисление
. Действительно, вычисление
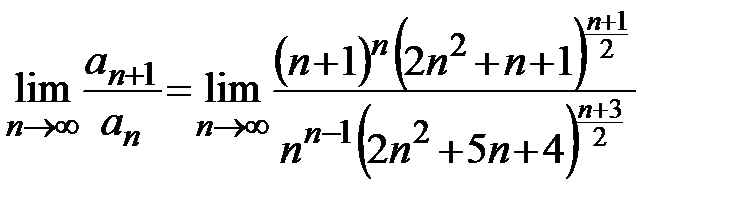
явно громоздко и проводить его не будем. Применим для анализа данного ряда признак Коши. Так как
 ,
,
то 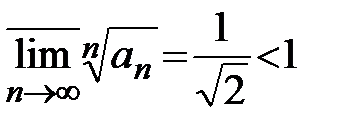 , следовательно, данный ряд сходится.
, следовательно, данный ряд сходится.
Пример 19. Рассмотрим ряд 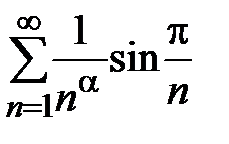 .
.
Так как 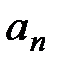 ~
~  и этот ряд сходится при
и этот ряд сходится при  и расходится при
и расходится при  как обобщенный гармонический ряд.
как обобщенный гармонический ряд.
Пример 20. Рассмотрим ряд 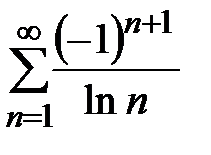 . Ряд
. Ряд 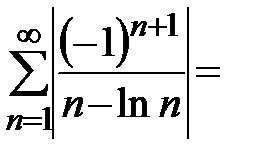
 расходится по признаку разреженности. Последовательность
расходится по признаку разреженности. Последовательность  положительна и стремится к нулю при
положительна и стремится к нулю при  , то ряд сходится условно по признаку Лейбница.
, то ряд сходится условно по признаку Лейбница.
Пример 21. Рассмотрим ряд. 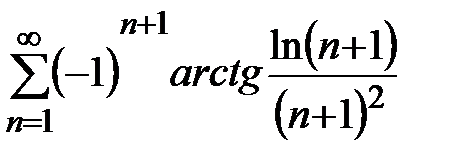 Так как
Так как  и
и 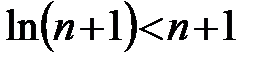 для
для  , то
, то 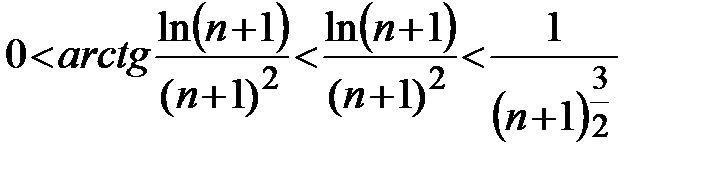 ,
, 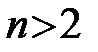 . Из этого неравенства в силу признака сравнения следует, что ряд
. Из этого неравенства в силу признака сравнения следует, что ряд 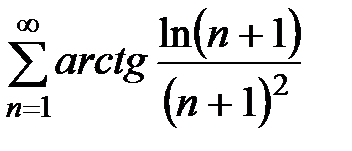 сходится, следовательно, данный ряд сходится абсолютно.
сходится, следовательно, данный ряд сходится абсолютно.
Пример 22. Рассмотрим ряд  . При любом
. При любом  для достаточно больших
для достаточно больших  имеем, что
имеем, что  . Для исследования сходимости ряда
. Для исследования сходимости ряда 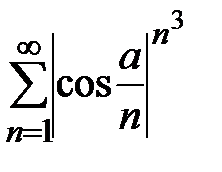 используем радикальный признак Коши. Так как
используем радикальный признак Коши. Так как
 ,
,
 .
.
Следовательно, ряд 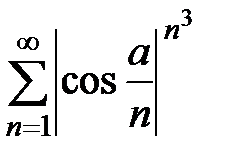 сходится при
сходится при 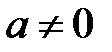 . Если же
. Если же 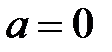 , то
, то 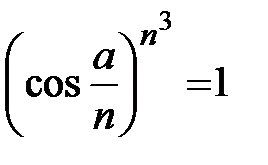 для всех
для всех  , т. е. не выполнен необходимый признак сходимости и ряд
, т. е. не выполнен необходимый признак сходимости и ряд  расходится. Итак, данный ряд абсолютно сходится при
расходится. Итак, данный ряд абсолютно сходится при 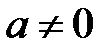 и расходится при
и расходится при 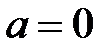 .
.
Пример 23. Рассмотрим ряд 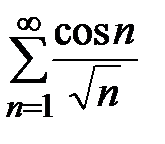 . Простейшая оценка
. Простейшая оценка 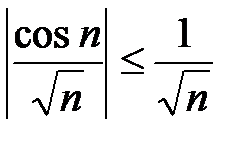 не дает информацию о поведении ряда
не дает информацию о поведении ряда  . Покажем, что данный ряд сходится. Положим
. Покажем, что данный ряд сходится. Положим  и
и  , тогда
, тогда  , а последовательность
, а последовательность 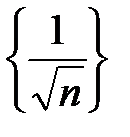 монотонно стремится к нулю при
монотонно стремится к нулю при 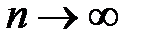 . В силу признака Дирихле данный ряд сходится. Для исследования абсолютной сходимости этого ряда удобно воспользоваться оценкой
. В силу признака Дирихле данный ряд сходится. Для исследования абсолютной сходимости этого ряда удобно воспользоваться оценкой 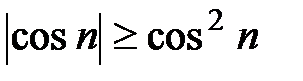 . Имеем:
. Имеем: 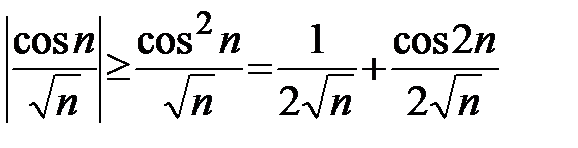 . Ряд
. Ряд  так же, как и исходный ряд, сходится в силу признака Дирихле, а ряд
так же, как и исходный ряд, сходится в силу признака Дирихле, а ряд  расходится. Следовательно, расходится ряд
расходится. Следовательно, расходится ряд  , а в силу теоремы сравнения и ряд
, а в силу теоремы сравнения и ряд 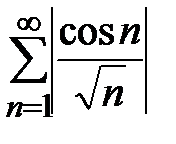 . Итак, ряд
. Итак, ряд 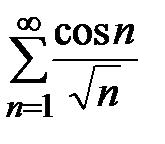 сходится условно.
сходится условно.
Пример 24. Рассмотрим ряд 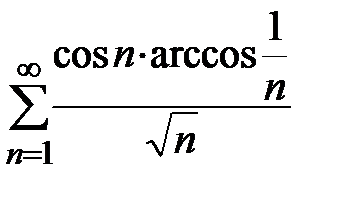 . Простейшая оценка
. Простейшая оценка  не дает информации о поведении ряда
не дает информации о поведении ряда  . Покажем, что данный ряд сходится. Положим
. Покажем, что данный ряд сходится. Положим 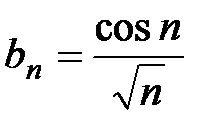 и
и 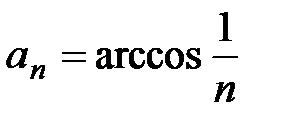 . Условная сходимость ряда
. Условная сходимость ряда 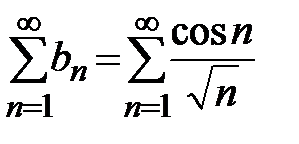 установлена в предыдущем примере. Так как последовательность
установлена в предыдущем примере. Так как последовательность 
 монотонна и ограничена,
монотонна и ограничена, 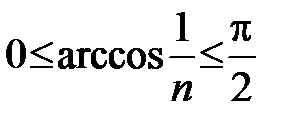 , то в силу признака Абеля данный ряд сходится. Расходимость ряда
, то в силу признака Абеля данный ряд сходится. Расходимость ряда 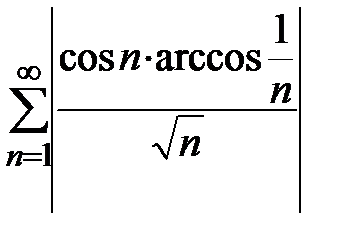 следует из неравенства
следует из неравенства 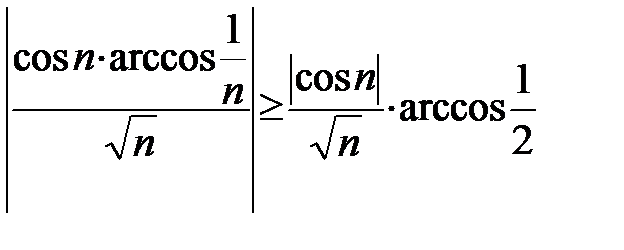
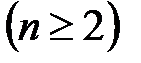 и расходимости ряда
и расходимости ряда  .
.
Итак, ряд 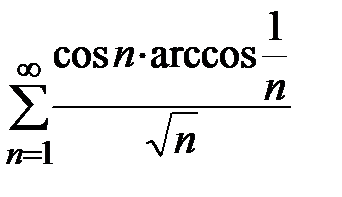 сходится условно.
сходится условно.