
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. Прямая линия в пространстве может занимать различные положения относительно плоскостей проекций.
|
|
Прямая линия в пространстве может занимать различные положения относительно плоскостей проекций.
Прямая общего положения – это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций (рисунок 7).

Рисунок 7 – Прямая общего положения
Прямые частного положения могут быть параллельны одной или двум плоскостям проекций.
1. Прямые, параллельные одной из плоскостей проекций, называются линиями уровня:
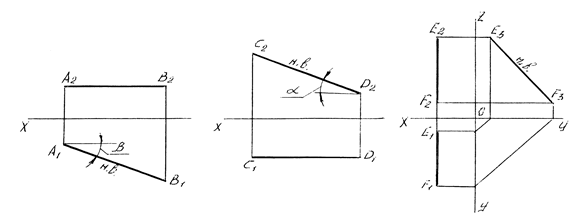
горизонталь – это прямая, параллельная плоскости проекций П1, ее горизонтальная проекция равна натуральной величине отрезка (рисунок 8 а);
фронталь – это прямая, параллельная плоскости проекций П2, ее фронтальная проекция равна натуральной величине отрезка (рисунок 8 б);
профильная прямая – это прямая, параллельная плоскости проекций П3, ее профильная проекция равна натуральной величине отрезка (рисунок 8 в).
а б в
Рисунок 8 – Прямые, параллельные одной плоскости проекций
а – горизонталь, б – фронталь, в – профильная прямая
2. Прямые, параллельные двум плоскостям проекций (или перпендикулярные к одной из плоскостей проекций), называются проецирующими прямыми:
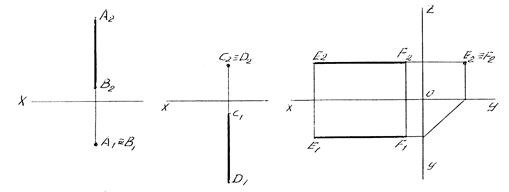
горизонтально-проецирующая прямая параллельна плоскостям проекций П2 и П3, т е перпендикулярна к плоскости П1 (рисунок 9 а);
фронтально-проецирующая прямая параллельна плоскостям проекций П1 и П3, т.е. перпендикулярна к плоскости П2 (рисунок 9 б);
профильно-проецирующая прямая параллельна плоскостям проекций П1 и П2, т.е. перпендикулярна к плоскости П3 (рисунок 9 в).
а б в
Рисунок 9 – Прямые, параллельные двум плоскостям проекций
а – горизонтально-проецирующая, б – фронтально-проецирующая,
в – профильно-проецирующая
Натуральную величину отрезка прямой линии общего положения определяют как гипотенузу прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – абсолютная величина алгебраической разности расстояний от концов другой проекции отрезка до оси проекций.
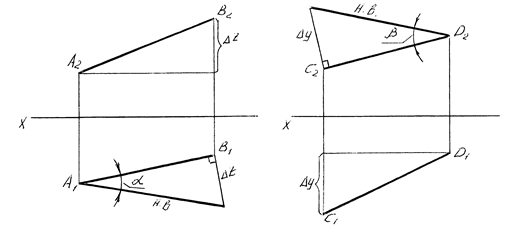
На рисунке 10 а показано построение натуральной величины отрезка АВ на горизонтальной плоскости проекций. Угол между проекцией отрезка и его натуральной величиной равен углу наклона самого отрезка к горизонтальной плоскости проекций – α.
На рисунке 10 б показано построение натуральной величины отрезка АВ на фронтальной плоскости проекций. Угол между проекцией отрезка и его натуральной величиной равен углу наклона самого отрезка к фронтальной плоскости проекций – β.
а б
Рисунок 10 – Определение натуральной величины отрезка прямой
а – на горизонтальной плоскости проекций, б – на фронтальной плоскости проекций
Деление отрезка в заданном отношении. Одним из свойств прямоугольного проецирования является то, что отношение отрезков прямой линии равно отношению их проекций. Если точка делит отрезок в пространстве в отношении 2: 3, то и проекции этой точки делят отрезок в том же отношении. На рисунке 11 показано деление отрезка АВ точкой С в отношении 2: 3. Для этого проводится произвольная прямая из любого конца отрезка на любой проекции, на ней откладываем 5 (2 + 3) произвольно выбранных одинаковых частей, точку 5 соединяем с другим концом отрезка и через точку 2 проводим прямую параллельную 5В1, до пересечения с А1В1, получаем горизонтальную проекцию точки С – С1, а затем по линии связи находим фронтальную проекцию точки С – С2.
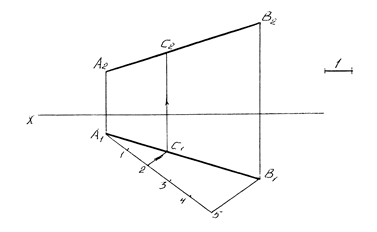
Рисунок 11 – Деление отрезка в заданном отношении
Следами прямой называют точки пересечения прямой с плоскостями проекций. М – горизонтальный след, N – фронтальный след прямой. Чтобы найти горизонтальный след прямой, надо продлить фронтальную проекцию отрезка до пересечения с осью X, а для того, чтобы найти фронтальный след прямой, надо продлить горизонтальную проекцию отрезка до пересечения с осью X. На рисунке 12 показано построение следов отрезка прямой АВ.

Рисунок 12 – Построение следов отрезка прямой АВ
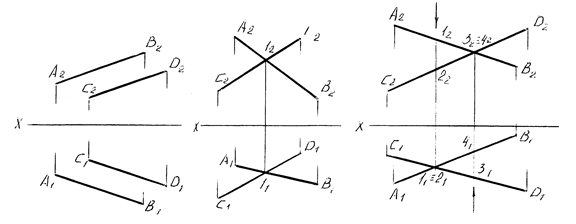
Взаимное положение прямых. Если прямые параллельны, то параллельны их одноименные проекции (рисунок 13 а), если прямые пересекаются, то точка пересечения их проекций лежит на одном перпендикуляре к оси X (рисунок 13 б), если прямые не параллельны и не пересекаются между собой, то они называются скрещивающимися (рисунок 13 в). Точки пересечения проекций этих прямых 1, 2 и 3, 4 называются конкурирующими точками. 1, 2 – горизонтально-конкурирующие, 3, 4 – фронтально-конкурирующие.
а б в
Рисунок 13 – Взаимное положение прямых
а – параллельные прямые, б – пересекающиеся прямые,
в – скрещивающиеся прямые
Теорема о проецировании прямого угла. Прямой угол, у которого хотя бы одна сторона параллельна какой-либо плоскости проекций, проецируется на эту плоскость в виде прямого же угла. Если прямая АВ параллельна горизонтальной плоскости проекций и на нее необходимо опустить перпендикуляр из точки С, то на горизонтальную проекцию этот угол проецируется в натуральную величину (рисунок 14).
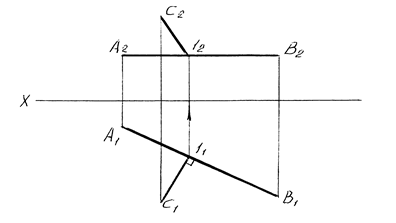
Рисунок 14 – Проецирование прямого угла