
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. Плоскость на чертеже может быть задана различными способами: тремя точками, не лежащими на одной прямой; прямой и точкой
|
|
Плоскость на чертеже может быть задана различными способами: тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на этой прямой; двумя параллельными прямыми; двумя пересекающимися прямыми; любой плоской геометрической фигурой; следами (рисунок 15).
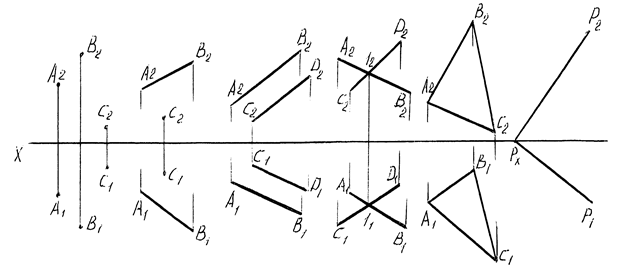
Рисунок 15 – Способы задания плоскостей
Плоскость, произвольно наклоненную к плоскостям проекций, называют плоскостью общего положения (все плоскости на рисунке 15).
Плоскости, перпендикулярные или параллельные плоскостям проекций, называются плоскостями частного положения.
Плоскости, перпендикулярные к плоскостям проекций, называются проецирующими (рисунок 16).
а б в
Рисунок 16 – Плоскости, перпендикулярные к плоскостям проекций
а – горизонтально-проецирующая, б – фронтально-проецирующая,
в – профильно-проецирующая
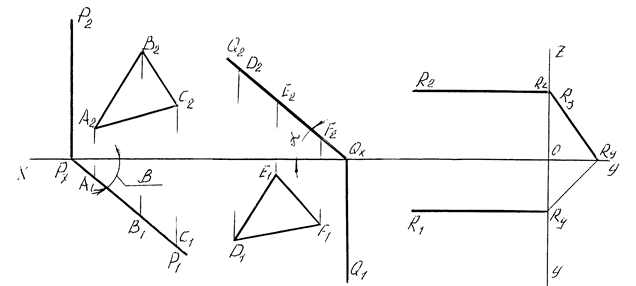
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня (рисунок 17).
а б в
Рисунок 17 – Плоскости, параллельные плоскостям проекций
а – горизонтальная, б – фронтальная, в – профильная
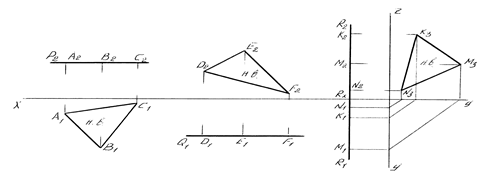
Точка принадлежит плоскости, если она расположена на какой-либо линии этой плоскости (рисунок 18 а). Прямая принадлежит плоскости, если она имеет с плоскостью две общие точки (рисунок 18 б).
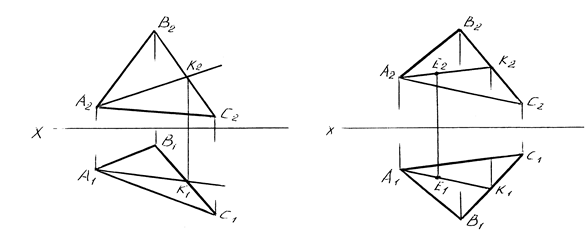
а б
Рисунок 18 – Принадлежность плоскости
а – точки, б – прямой
Некоторые прямые в плоскости могут занимать особое положение – это главные линии плоскости:
- горизонталь h параллельна плоскости П1 (рисунок 19а);
- фронталь f параллельна плоскости П2 (рисунок 19б);
- линия наибольшего ската плоскости – это перпендикуляр к горизонтальному следу плоскости (рисунок 19 в).
 а б в
а б в
Рисунок 19 – Главные линии плоскости
а – горизонталь, б – фронталь, в – линия наибольшего ската плоскости
Параллельность прямой линии и плоскости. Параллельность плоскостей. Прямая и плоскость параллельны, если в плоскости можно провести прямую, параллельную заданной плоскости (рисунок 20а). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (рисунок 20б). Если плоскости заданы следами, то должны быть параллельны их одноименные следы (рисунок 20 в).

а б в
Рисунок 20 – Взаимное положение прямой и плоскости, плоскостей
а – параллельность прямой и плоскости, б – параллельность плоскостей, заданных не следами, в – параллельность плоскостей, заданных следами
Пересечение плоскостей. Две плоскости пересекаются по прямой линии. Для построения этой прямой необходимо найти две точки, общие для пересекающихся плоскостей, или же найти одну такую точку и направление прямой. На рисунке 21 приведены примеры построения линии пересечения плоскостей, заданных следами.
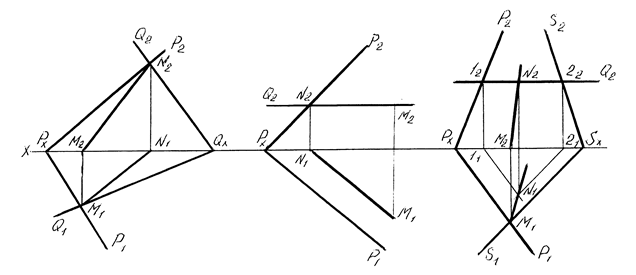
Рисунок 21 – Построение линии пересечения плоскостей
Пересечение прямой с плоскостью. Для того, чтобы построить точку пересечения прямой с плоскостью, выполняют следующие построения:
- заданную прямую заключают во вспомогательную плоскость частного положения Q;
- строят линию пересечения заданной и вспомогательной плоскостей (прямая МN);
- на пересечении прямых – заданной и построенной – находят искомую точку К.
На рисунке 22 приведены примеры построения точки пересечения прямой с плоскостью.

Рисунок 22 – Построение точки пересечения прямой с плоскостью