Лабораторная работа №3.

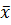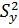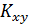1. По данным выборок и вариационных рядов (зад. 2, лаб.1) определить статистические оценки математического ожидания (, ), дисперсии , , среднего квадратического отклонения , , ковариации и коэффициента корреляции ().

Определение параметров по выборке для случайной величины Х.

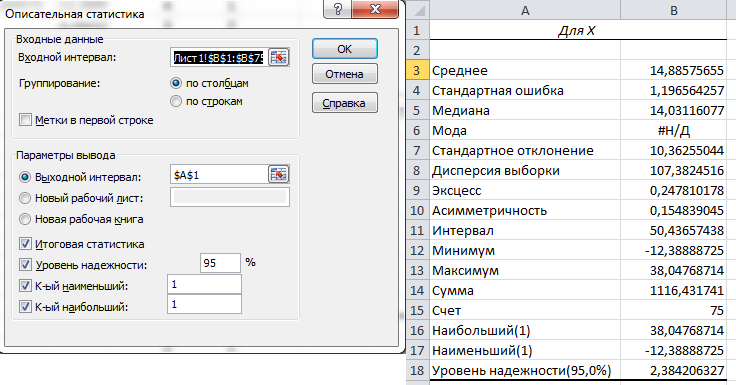
Рисунок 1 – Статистическая оценка математического ожидания (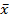), дисперсии 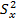, среднего квадратического отклонения

Определение параметров по выборке для случайной величины Y.

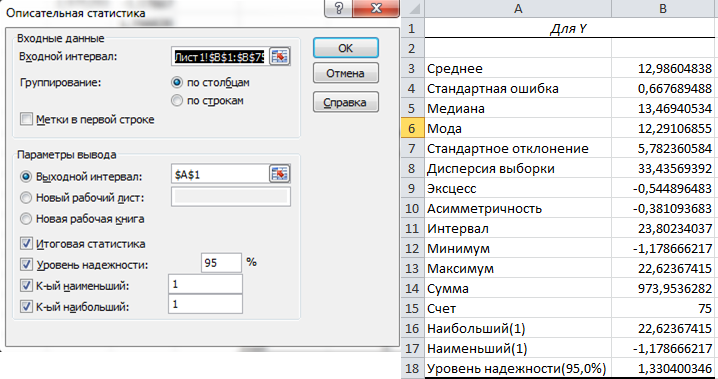
Рисунок 2 – Статистическая оценка математического ожидания (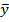), дисперсии , среднего квадратического отклонения

Определение параметров по вариационному ряду для случайной величины X.

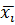
	-9, 236	-2, 932	3, 372	9, 677	15, 98	22, 286	28, 59	34, 895

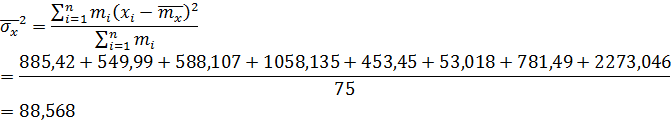
Определение параметров по вариационному ряду для случайной величины Y.

	0, 309	3, 283	6, 259	9, 234	12, 209	15, 185	18, 160	21, 135

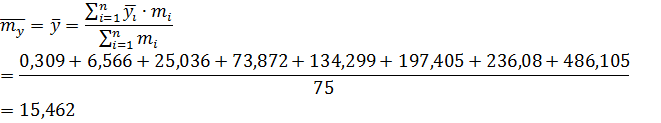
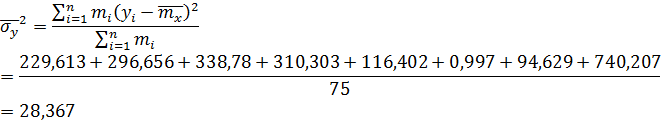
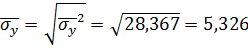
По данным выборок X, Y определим ковариацию 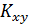и коэффициент

корреляции ().

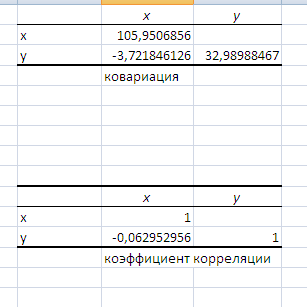
Рисунок 3 – Результат ковариации и коэффициента корреляции

2. Построить доверительные интервалы для статистических оценок математического ожидания, дисперсии, среднего квадратического отклонения (зад.2, лаб.1).

Определение доверительного интервала для статистических оценок математического ожидания.

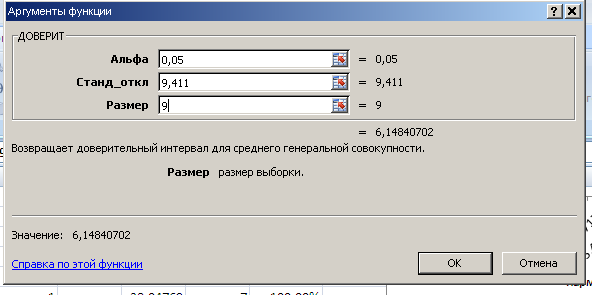
Рисунок 4 – Использование функции ДОВЕРИТ для случайной величины X

При .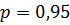

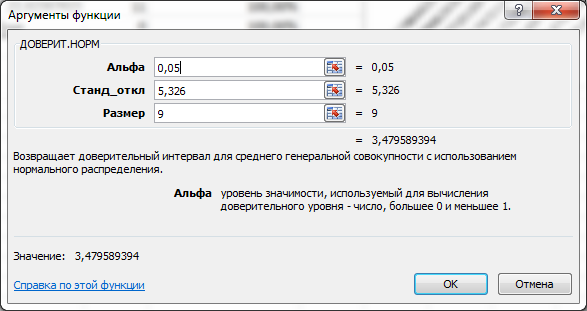
Рисунок 5 – Использование функции ДОВЕРИТ для случайной величины Y

При .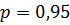

Определение доверительного интервала для дисперсии случайной величины X.

По величине доверительной вероятности определяем величины , .

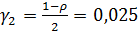По величинам , и определяем , .

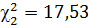Определяем границы доверительного интервала:

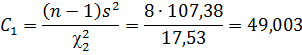
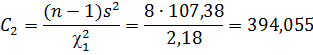
49, 003< 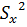< 394, 055

Среднее квадратическое отклонение для случайной величины X: 7, 0002< < 19, 85.

Определение доверительного интервала для дисперсии случайной величины Y.

По величине доверительной вероятности определяем величины , .

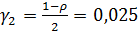По величинам , и определяем , .

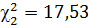Определяем границы доверительного интервала:

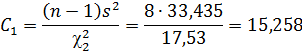
15, 258< 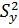< 122, 697

Среднее квадратическое отклонение для случайной величины Y: 3, 906< < 11, 076.