Относительное обоснование суждений

Относительное обоснование суждения есть установление его правдоподобности или истинности на основе знания истинности других суждений. Суждения, на основе которых обосновывается некоторое суждение, называются посылками, а суждение, которое обосновывается, называют заключением. Из посылок заключение следует по правилам логики.

Правила логики можно подразделить на два класса: индуктивные и дедуктивные. В соответствии с этим подразделим и относительное обоснование на индуктивное и дедуктивное обоснования. Рассмотрим методы каждого из этих обоснований.

(2А) Индуктивный метод обоснования истинности суждения.

Этот метод представляет установление на основе истинности посылок правдоподобности заключения. Логические правила, по которым происходит такое обоснование, называют индуктивными правилами. Это правила индуктивной логики. К ним относятся: неполная индукция, аналогия, правила Милля, фундаментальная индуктивная схема т.п. Рассуждения по этим правилам называются правдоподобными рассуждениями, т.к. они не обеспечивают 100% истинности выводного суждения, а сами правила – схемами правдоподобных рассуждений [45]. Все индуктивные правила являются неформальными, т.е. содержательными правилами. Это значит, что если мы не знаем содержания посылок (того, что и о чем они говорят), то нельзя гарантировать даже какой-то степени истинности заключения, а значит, можно получить заведомую ложь. Последнее будет видно при рассмотрении конкретных индуктивных правил и соответствующих им обоснований, например, следующих:

(2А1) Обоснование по методу неполной индукции имеет схему P (a₁), P(a₂), …, P(a_n) 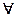x P(x). Схема показывает, что, если суждения о том, что объект а₁ обладает свойством Р и т.д. вплоть до энного объекта, который тоже обладает этим свойством, истинны, то суждение о том, что все объекты данного класса обладают свойством Р, т.е. 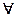x P(x), правдоподобно. Это значит, что суждение 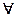x P(x) может иметь некоторую степень истинности, но может быть и ложным.

Но чтобы заведомо не получать ложь, чтобы были шансы по этому правилу получить хотя бы правдоподобное заключение, необходимо знать, о каких объектах /а₁,..., а_n/ и что /Р/ мы утверждаем. Например, нет никакого смысла применять правило неполной индукции к такому случаю: первый встретившийся человек – писатель, второй – тоже, энный – тоже. Тогда получится, что все люди – писатели, что заведомо неверно, и никакой правдоподобности нет. Поэтому знать содержание посылок P(a₁), …, P(a_n) необходимо. Отсюда данное индуктивное правило содержательное, а не формальное, о котором мы выше скажем подробнее.

Если посылки будут истинными суждениями о смертности встретившихся нам людей, то заключение по правилу неполной индукции будет правдоподобным. Уже иными методами можно обосновать, что оно не только правдоподобно, но и истинно, даже не просто истинно, но и необходимо истинно. История науки знает немало случаев, когда полученные по правилу неполной индукции выводы, считавшиеся правдоподобными, оказались ложными. К ним относится долго бытовавшее в Европе мнение о том, что все лебеди белые, полученное на основе наблюдения европейских лебедей.

(2А2) Обоснование по методу аналогии. Его схема такая: если суждения Р¹(а),..., Р^n-1(а), Р⁽ⁿ⁾ (а) истинны, и если суждения Р¹(b), …, Р^n-1(b) тожеистинны, то суждение Р⁽ⁿ⁾(b) правдоподобно. Пример: рядом химических элементов обладают как Солнце, так и Земля. Это истинные посылки. Когда на Солнце был открыт гелий, к истинным посылкам прибавилось утверждение об обладании Солнцем данным элементом. Отсюда был сделан вывод о правдоподобности обладания гелием и Землей. Затем была установлена эмпирически истинность этого суждения.

(2А3) Обоснование методом фундаментальной индуктивной схемы. Схема такова: если истинны суждение " если А, то В" и суждение " В", то суждение " А" правдоподобно. Заметим, что в суждении " если А, то В" не утверждается истинность А, а утверждается зависимость В от А. Тогда подтверждение следствия В придает правдоподобность гипотезе (предположению) А, но не обосновывает ее истинности. Правило это содержательное, ибо без знания конкретного содержания суждений его применение не имеет смысла.

Если подтверждается очень маловероятное следствие В, то это дает очень большую степень правдоподобности гипотезе А. Вообще из гипотезы А можно получать разные заключения В₁,..., В_n. И чем больше будет подтверждаться истинность этих заключений и чем они будут более маловероятны, тем больше будет подтверждаться правдоподобность гипотезы А. Так что данный метод является методом подтверждения гипотез.

(2А4) Частным видом индуктивного обоснования суждений являются индуктивные методы Милля. Индуктивны они потому, что из истинных посылок дают только лишь правдоподобные заключения. Специфика обосновываемых суждений состоит в том, что это суждения о существовании обусловливающих связей.

Сам Д.С. Милль считал свои методы методами обнаружения причинных связей. Таковыми они считаются и в учебниках по логике. При этом причинная связь понимается гораздо шире, чем это имеет место в физике по отношению к объективной причинной зависимости. В физическом мире материальные явления могут обусловливать возникновение других явлений только с помощью физических взаимодействий. Поэтому такое обусловливание одних явлений другими правомерно называть физической причинностью, которая всегда материальна.

Если же понимать под причиной и следствием явления такие, что, если имеет место первое явление, то имеет место и второе, а если нет первого, то нет и второго[46], то это просто связь обусловливания, и не обязательно физически причинная и даже не обязательно материальная. Это просто функциональная зависимость, и не обязательно причинная.

Поэтому методы Милля (единственного сходства и различия и т.п.) могут рассматриваться далеко не только как методы обнаружения причинных зависимостей, а просто как методы, позволяющие с какой-то степенью правдоподобия судить о наличии вообще какой-либо зависимости. Во всяком случае, гарантировать причинную зависимость они не могут никак.

(2Б) Дедуктивный метод обоснования суждения является доказательством истинности этого суждения путем его выведения из истинных посылок с помощью формальных (дедуктивных) правил дедуктивной логики. Формальный характер этих правил состоит в том, что их применение не зависит от знания содержания ни посылок, ни заключения. Каково бы ни было это содержание, если посылки истинны, то и обосновываемое заключение будет истинным. Например, по правилу " модус поненс" из " А" и " Если А, то В" следует заключение " В". И если суждения " А" и " Если А, то В" истинны, то суждение " В" будет всегда истинно. Такое обоснование суждения В не требует знания конкретного содержания посылок. Каковы бы они ни были, заключение будет истинным.

Причины разнообразия формальных логик различны. Одной из них является то, что, как мы говорим, сама истинность плюралистична. Это предопределяет пригодность той или иной системы логических правил обеспечивать получение из истинных (в каком-либо смысле истинности) суждений снова истинных суждений (в этом же самом смысле истинности).

Общеизвестным примером в этом случае являются понятия классической и конструктивной истинности. Классическая истинность характерна тем, что предполагает только две оценки истинностного значения суждения - истину и ложь. При этом не существенно, имеется ли эффективный (точнее – конструктивный) метод установления истинности. Это значит, что приемлем способ обоснования истинности каким-либо косвенным путем. Например, допустим, что нам надо обосновать истинность суждения о существовании некоторого объекта. Тогда предположим, что он не существует. Если, исходя из этого предположения, придем к противоречию, то по правилу доказательства от противного обоснуем истинность суждения о существовании данного объекта. Но при этом может не иметься никакого способа, как этот объект найти или как его построить.

Конструктивная истинность предполагает непременное наличие способа построения объекта, о существовании которого утверждается в обосновываемом суждении. Это не означает, что должны иметься материальные условия построения объекта. Их может и не быть. Но способ (метод) обязательно должен быть явно представлен.

Оказывается, чтобы на основе истинности посылок обосновать истинность заключения, нужны разные логические системы формальных правил для классической и конструктивной истинности. Для классической истинности нужна классическая логика, а для конструктивной истинности – конструктивная.

Таким образом, классическая логика – это система правил, преобразующая логическую форму суждений, но сохраняющая их классическую истинностную оценку. Иными словами, это логика, дающая из классически истинных суждений только классически истинные суждения. Однако классическая логика не сохраняет конструктивной истинностной оценки. Поэтому, чтобы логика сохраняла конструктивную истинность, необходимо перестроить систему классической логики. В результате строится конструктивная логика, которая сохраняет значение конструктивной истинности, т.е. из конструктивно истинных высказываний по правилам этой логики получаются только конструктивно истинные высказывания.

Если, допустим, надо сохранять иную оценку суждений, нежели истинность, то строится особая логическая система и т.д. Однако обоснования суждений в обычных науках в основном обходятся классической логикой. Поэтому в качестве примера формальных правил классической логики приведем нижеследующие:

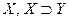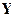├ . Это знакомое нам правило, называемое " модус поненс". Знак 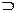означает связку " если…, то…", знак ├ - следует, 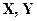- высказывания.

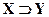, ù Y ├ ù 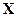, где ù - логическое отрицание. Правило " модус толленс".

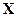├ , где знак 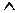означает союз " и".

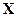├ , где знак 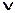означает союз " или".

ù ù ├ .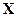

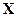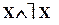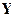├ . Это правило сообщает о том, что, если в теории имеется противоречие, то будет доказуемо в ней любое суждение, которое можно записать на языке данной теории. С другими правилами можно познакомиться по любому учебнику математической логики, которая и описывает системы логических правил дедуктивных логик. Аристотелевская и математическая логики – это искусственные построения, весьма незначительно отражающие процессы реального мышления. Математическая логика – это разнообразные исчисления, одно из которых (логика предикатов) находит очень незначительное применение к правилам мышления. Аристотелевская логика – тоже искусственное построение (в основном - силлогистика), которое тоже весьма незначительно относится к мышлению.

Теперь обратим внимание на то, что относительное обоснование есть вывод, который может быть как предметным выводом, т.е. выводом на основе свойств самого предмета, о котором мы рассуждаем, так и выводом аксиоматическим, т.е. выводом из аксиом [47]. Например, " великая теорема Ферма" была (если только она была) не выводом из аксиом, так как арифметика еще не была аксиоматизирована, а предметным выводом на основе анализа свойств предмета арифметики, т.е. натуральных чисел. Это совершенно различные выводы и их нельзя путать.

Итак, мы показали разнообразие методов обоснования суждений, которое можно наглядно представить следующей схемой:

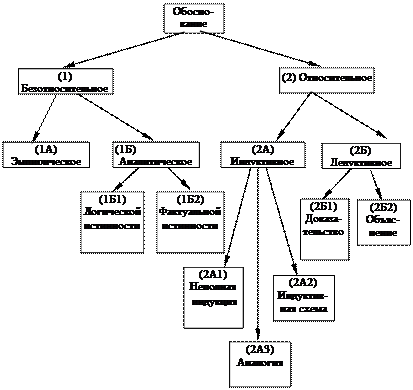Возможность и необходимость применения тех или иных методов обоснования истинности (или правдоподобности) зависит от конкретного содержания суждений, от поставленных перед обоснованием задач, от возможностей применения тех или иных методов обоснования. Обоснование суждений важно само по себе, и его методами необходимо уметь пользоваться. Оно приобретает более сложный характер, когда возникает потребность обоснования теорий. На этом вопросе мы подробнее остановимся в главе V.

До сих пор мы говорили об обосновании истинности простых суждений. Этой проблемой логика не занимается, она предполагает данную проблему решенной. Это дело методологии науки. Зато истинность сложных суждений – это уже компетенция логики. И если известны истинностные значения простых суждений, то, используя уже известный табличный метод, можно вычислить истинностное значение любого сложного суждения.

Пусть, например, дано суждение формы 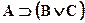и известно, что А=И, В=И, С=И. Тогда 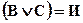. Но тогда 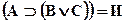. Аналогичным образом можно обосновывать истинность (или ложность) сколь угодно больших сложных суждений.