
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Семиотическая типология научных языков
|
|
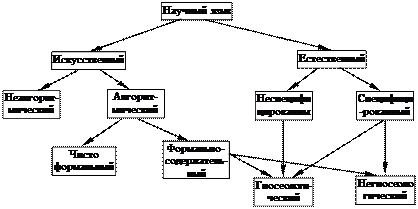 |
А теперь охарактеризуем каждый из типов научных языков, представленных в этой схеме. Не будем только останавливаться на естественном неспецифицированном языке, так как это обычный разговорный язык, который достаточно описан во всякого рода грамматиках.
Естественный специфицированный язык – это естественный язык, который дополняется специальными научными терминами (научной терминологией). Некоторые науки публикуют перечни своих научных терминов в виде словарей или энциклопедий (математическая, физическая, медицинская, философская энциклопедии и т.п.). На сводный каталог терминов многих наук претендуют общенаучные энциклопедии вроде БСЭ.
Метод построения специфицированного языка:
За основу выбирается естественный язык.
Уточняются с помощью эффективных определений некоторые термины этого языка. Добавляются новые специальные термины для отображения специфических свойств действительности, доступных только научному (но не обыденному) познанию, или для обозначения специального рода абстрактных объектов, вводимых наукой.
При этом грамматика и основной словарный состав языка берутся у обычного разговорного языка. Примеров специфицированных языков достаточно много. Фактически ими являются языки естественных и гуманитарных наук. Например, в языке физики такие термины естественного языка как " масса", " сила", " ускорение" из чисто качественных превращены в количественные, позволяющие делать вычисления. А также введены термины, не фигурирующие в обычном естественном языке: " протон", " нейтрон", " кварк", " виртуальная частица" и т.п. Однако построение терминов и предложений, распознавание их, отличение правильно построенных слов от неправильно построенных остается таким же, как в естественном языке.
Искусственные языки создаются для решения определенных проблем научной теории. Как разговорные языки они не употребляются. При построении искусственного языка естественный язык используется как средство мышления, необходимое для осуществления процесса построения. Но сам искусственный язык строится по совсем другим правилам построения, нежели естественный язык.
Прежде всего, искусственный язык отличается от естественного своими синтаксическими правилами построения. Эти правила не зависят от знания семантики слов языка. В типологии научных языков мы выделили искусственные неалгоритмические языки, синтаксические правила построения которых не являются алгоритмами. В настоящее время такие языки почти не применяются и мы на них более подробно останавливаться не будем. Зато огромное значение приобрели алгоритмически построенные языки.
Алгоритмически построенный язык – это язык, слова которого распознаются только формальными синтаксическими правилами. Чтобы пояснить особенность этих правил, представим, что из алфавита языка мы образовали все возможные строчки символов. Теперь из этого множества строчек символов нам надо отобрать строчки, являющиеся словами языка. В алгоритмически построенном языке для этого существует правило (алгоритм), согласно которому только по форме строчек символов, без всякой опоры на семантику, можно точно установить, принадлежит ли взятая строчка символов языку или не принадлежит. Для естественного языка это сделать невозможно. В силу такой специфики распознавания слов языка алгоритмический язык является формальным языком, а естественный язык – содержательным (неформальным).
В настоящее время построено много самых различных формальных языков. Например, в логике построены формальные языки различных логик. В математике построены формальные языки почти всех математических теорий, например, язык алгебры. Для этого языка синтаксические правила построения представляют алгоритм, согласно которому строчка символов " 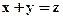 " относится к языку алгебры, а строчка "
" относится к языку алгебры, а строчка "  " не относится. И этот вопрос решается без всякого знания того, что обозначают символы
" не относится. И этот вопрос решается без всякого знания того, что обозначают символы 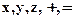 .
.
Метод построения формального языка следующий:
Выбирается алфавит.
Задаются формальные синтаксические правила построения слов в данном алфавите.
При необходимости знакам алфавита и словам языка может придаваться интерпретация (т.е. семантика).
Если формальному языку семантика не придается, то он называется чисто формальным языком. Если семантика придается, то он становится формально-содержательным языком. Формальным он остается потому, что его слова как до, так и после интерпретации продолжают распознаваться (строится) по чисто формальным синтаксическим правилам. Содержательным такой язык именуется в силу того, что его слова приобретают семантику. Здесь принимается во внимание то обстоятельство, что в языковых системах форма системы задается синтаксисом, а содержание - семантикой.
В связи с созданием искусственных языков возникла проблема отношения языка к действительности. Ясно, что чисто формальный язык непосредственно действительности не отображает (нет семантики). Но он все же строится с учетом того, чтобы построенные в результате интерпретации на его основе содержательные языки могли выполнять функцию отображения действительности.
Содержательные языки могут иметь двоякого рода семантику (в области теоретических и в области материальных объектов), а потому могут по-разному относиться к действительности. Областью интерпретации может быть, во-первых, система теоретических (абстрактных) объектов, в объективной (материальной) действительности не существующих. Например, такой системой может быть математическая система, в частности, какая-либо числовая система или система геометрических объектов (точек, линий, плоскостей с соответствующими отношениями). Но может быть и система теоретических объектов физической теории, например, система материальных точек, бесконечно больших скоростей, инерциальных систем измерения, в объективной действительности тоже не существующих. Областью интерпретации формального языка может быть и система материальных объектов.
В зависимости от области интерпретации языки могут подразделяться на негносеологические и гносеологические. Негносеологический язык – это формальный язык, имеющий интерпретацию на области системы абстрактных объектов. Гносеологический язык является языком, имеющим интерпретацию на области материальных объектов. Он может быть эмпирическим языком. Ясно, что один и тот же формальный язык может (в зависимости от рода интерпретации) быть негносеологическим или гносеологическим. Хорошо известный пример – это логический язык исчисления высказываний, который может иметь и арифметическую интерпретацию (язык так называемой 2 – арифметики), и электромеханическую интерпретацию (язык логики контактно-релейных схем).
В итоге мы рассмотрели языки, представленные как семиотические системы, т.е. как системы символов с синтаксическими правилами построения и семантическими правилами обозначения. Для анализа научных языков семиотический подход весьма важен. Но важен также и логический подход, с точки зрения которого язык рассматривается как логическая система.
Язык как логическая система представляет множество слов с логическими отношениями между ними, задаваемыми логическими правилами определения и преобразования. Правила определения говорят о том, как правильно на основе одних терминов языка определять другие его термины. Правила преобразования позволяют из одних истинных предложений получать другие истинные предложения. Как в обыденных, так и в научных рассуждениях мы этим постоянно пользуемся независимо ни от каких теорий. Поэтому логические правила выполняют в этом случае функцию логики языка.
Ясно, что, пользуясь правилами определения и преобразования, мы используем логику языка, каким бы ни был этот язык (естественным или искусственным). Из самого способа использования этой логики следует, что это логика дедуктивная, о которой мы уже говорили. Главное состоит в том, чтобы мы всегда могли с помощью правил преобразования из истинных в каком-то смысле посылок при всех преобразованиях их форм получить истинные в этом же самом смысле заключения. Оказалось, что это довольно трудная проблема не только научного, но и обычного рассуждения.
Не вдаваясь в глубину этого вопроса, поясним это на примере из гуманитарной сферы. Допустим, идет суд, на котором обвинитель (прокурор) доказывает виновность подсудимого, а защитник – невиновность. Спрашивается, одной логикой или различными логиками должны пользоваться прокурор и защитник? Если " да", то какой? Обычной? А если нет, то какими логиками им надлежит пользоваться?
Чтобы ответить на этот вопрос, зададим частный вопрос. Например, такой: может ли прокурор, предположив, что подсудимый невиновен, придти к противоречию и тем самым доказать виновность подсудимого? Ведь это рассуждение есть рассуждение по правилу доказательства от противного обычной (классической) логики.
Однако суд такого обоснования виновности не примет. Он потребует представления всей цепочки событий, составляющих преступление, т.е. потребует реконструкции событий преступления. Этим самым суд не признает правомерность использованного прокурором правила доказательства от противного. Но тем самым суд не признает правомерность классической логики для рассуждений прокурора. Его логика не должна содержать вышеупомянутого правила. Но это требует создания какой-то особой логики прокурора, т.е. перестройки всей обычной логики.
Ситуации, требующие перестройки классической логики, возникли в обосновании математики. Под влиянием этого обстоятельства такая перестройка действительно была произведена. В итоге была создана конструктивная логика, не содержащая правила доказательства от противного. Вот этой-то логикой и может пользоваться прокурор.
А теперь посмотрим на логику защитника. Если защитник воспользуется правилом доказательства от противного и из предположения виновности подсудимого придет к противоречию, тем самым доказывая невинность, то суд ничего против этого обоснования иметь не будет. Стало быть, защитник может пользоваться классической логикой в своих рассуждениях. Тем самым можно констатировать наличие разных логик языка применительно к разговорному (естественному) языку.
Если посмотреть на рассуждения в математике, физике, то тоже можно увидеть, что бывают обстоятельства, в которых надо использовать разного рода логики языка. Например, могут быть случаи, когда в математике необходимо использовать конструктивную логику (если требуется конструктивное обоснование истинности суждений). Есть пример Рейхенбаха, когда в рассуждениях о квантовых объектах надо применять трехзначную (неклассическую) логику языка физики. Все это указывает на то, что логики естественного, так и искусственных языков бывают различными. Их выбор существенно зависит от того, какого рода истинностная оценка должна сохраняться правилами логики языка при преобразовании предложений этого языка. Возникает методологическая проблема выбора логики языка. Для ее решения можно воспользоваться следующим общим методом.
Выявить идеализации суждений (предложений) языка.
На этой основе установить тип, вид и вообще специфику истинности этих суждений.
Используя построенные формальной логикой логические исчисления, выбрать логику, которая при преобразовании суждений сохраняет данную специфику истинности.
Допустим, что мы имеем дело с логически истинными суждениями. Тогда мы можем пользоваться как известным уже нам правилом модус поненс (Из " А" и " Если А, то В" следует " В"), так и правилом подстановки (если в истинное сложное суждение вместо входящего в него суждения подставить другое, то получим снова истинное суждение). Но если мы имеем дело с фактуально истинными суждениями, то правило модус поненс применять можно, а правило подстановки нельзя (иначе из истины можно получить ложь).
Не для всех фактуально истинных, так же как и не для всех логически истинных суждений применима одна и та же логика. Примеры на этот счет мы уже приводили. Поэтому в научном познании метод выбора логики языка иногда имеет не просто важное, а даже кардинальное значение.