
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава V. Методы гносеологического анализа теорий
|
|
Исследованию теорий различных семиотических типов посвящено огромное количество литературы. Анализ теорий чрезвычайно многоаспектен. Выбор аспектов существенно зависит от семиотического типа теорий. Например, анализ чисто формальных теорий имеет мало общего с анализом чисто содержательных (неформальных) гносеологических теорий.
Анализом теорий занимаются логика, семиотика, методология, философия, а также более специальные науки вроде науковедения, информатики и т.п. Все они имеют специфические задачи и соответствующие решению этих задач специальные методы исследования теорий. Знакомство со всем этим аналитическим арсеналом требует специальной подготовки и не может быть дано на базе только вышеизложенного материала. Поэтому мы ограничимся теми аспектами анализа теорий, для которых достаточно той методологической базы, с которой читатель уже был ознакомлен.
Обычные естественные и гуманитарные теории принадлежат к семиотическому типу чисто содержательных теорий. С ними читатель более всего знаком. Поэтому естественно дать изложение методов, предназначенных для анализа теорий именно этого типа. Это методы гносеологического анализа теорий.
Гносеология изучает отношение теории, как языкового образования, к объективной действительности. Отношение теории к системам абстрактных объектов, отношение одной теории к другой, отношение теории к языку, логические и семиотические свойства теорий изучает уже метатеория. Наиболее успешно разработана частного вида метатеория, относящаяся к математике и называемая метаматематикой. Поэтому изучение теории как отображения объективной действительности входит в компетенцию именно гносеологии. Главнейшей проблемой в этом изучении является проблема истинности.
Возникает проблема: что это за истинность, какого она семиотического типа, вида, индивидуальной специфики? Для ее решения необходимо исследование теории и в первую очередь изучение отношения теории к тому предмету, которым является область объектов, на которой законы теории истинны. Для этого и необходим метод гносеологического анализа предмета теории, который состоит в том, чтобы:
1. Выявить идеализаци, при которых теория отображает действительность.
2. Определить с помощью этих предпосылок непосредственный и опосредованный предметы теории. Опосредованный предмет теории - это та область объективной действительности, к решению задач относительно которой теория приложима. Это - область приложений теории. Непосредственный предмет теории - это система теоретических объектов, на которой теория (точнее - законы теории) интерпретируема. Это - область интерпретации теории. Ясно, что область интерпретации с точностью до определенных идеализаций приближается к области применимости теории, но все же это различные области. Законы любой теории имеют идеализированную интерпретацию. Материальную интерпретацию имеют приложения теории.
3. Исходя из специфики непосредственного и опосредованного предметов теории и принимаемых ей идеализаций, установить специфику истинности теории. Поясним действие метода гносеологического анализа более подробно и покажем его применение на конкретных примерах.
В главе III мы уже говорили о том, что теории, отображающие материальную действительность, являются гносеологическими теориями. Гносеологическая теория не может отобразить материальную действительность " так, как она есть сама по себе". Стало быть, отображение действительности «самой по себе» есть лишь недосягаемый предел ее отображения. А реально теория эту действительность отображает с точностью до определенных идеализаций. Но теория в то же время используется для решения практических задач, касающихся объективной действительности.
Поэтому теория имеет на самом деле два предмета. Во-первых, это - непосредственный предмет, представляющий систему теоретических объектов, с точностью до которых теория отображает объективную действительность. А, во-вторых, это опосредованный (непосредственным предметом) предмет, которым является сама отображаемая действительность, существующая вне и независимо от процесса ее отображения.
Ясно, что непосредственный и опосредованный предметы теории являются различными по своей природе системами. Первый - системой абстрактных (теоретических) объектов, второй - системой материальных объектов. Ясно также, что непосредственный предмет соотносится с опосредованным предметом теории лишь приблизительно, представляет его односторонне, а его специфика зависит от специфики задач, решаемых теорей.
Законы теории интерпретируются на системе теоретических объектов, представляющей непосредственный предмет теории. Поэтому истинность теории непосредственно является аналитической истинностью. Но так как теория применяется для решения задач, относящихся к объективной действительности, то опосредованно она эмпирически истинна. Но тогда аналитическая и эмпирическая истинности есть оценки отношения теории к разным ее предметам, и они не обязаны соответствовать друг другу.
Законы теории не могут формулироваться непосредственно для материальных систем. Все эти системы даже одного класса в действительности различны и индивидуальны. Для каждой системы законы не сформулировать. Законы формулируются лишь для того общего, а значит идеализированного, что существенно в изучаемых системах некоторого класса для решения определенных задач. Этим общим и является система теоретических объектов. Поэтому законы формулируются именно для систем теоретических объектов, а применяются с некоторой степенью приближения и точности для некоторого класса систем объективной действительности.
Конечно, у разных наук степень упрощения и идеализации областей материальной действительности различна. Относительно одних наук она мало заметна, а относительно других - чрезвычайно велика. Однако без упрощений и идеализаций не обходится ни одна наука. Чтобы продемонстрировать вышесказанное на каком-то конкретном примере, выберем средний вариант, который представляют, на наш взгляд, физические теории. В частности, теории механики.
Сформулируем нашу задачу относительно этих теорий более детально. Опосредованным предметом теорий механики является механическое движение материальных физических объектов. Возникает вопрос: как сформулировать законы, отображающие это движение? Для этого необходимо применить метод гносеологического анализа механического движения, упростить и идеализировать его так, чтобы созданные на этой основе теоретические термины и законы могли успешно применяться для решения задач, касающихся объективного механического движения.
Такого рода задачи бывают существенно различны. Поэтому существенно различны упрощения и идеализации механического движения. Но тогда будут существенно различны и законы, его описывающие (или отображающие).
Гносеологический анализ законов теории состоит в том, чтобы:
Выявить идеализации, при которых формулируется непосредственный предмет исследуемой теории.
Показать, что при этих идеализациях данные законы в области непосредственного предмета аналитически истинны.
Показать, что с помощью этих законов можно решать задачи, относящиеся к опосредованному предмету теории и тем самым …
показать эмпирическую истинность теории.
Чтобы продемонстрировать применение метода гносеологического анализа к теориям механики, мы воспользуемся уже известными результатами, ибо проделать всю эту работу полностью здесь не представляется возможным. Для экономности изложения в начале сделаем общий список идеализаций для всех рассматриваемых теорий механики, пронумеруем их, а при описании предпосылок конкретных теорий будем ссылаться только на эти номера, не переписывая самих предпосылок. Кроме того, так как предпосылки будут фактуально (а не логически) истинны, то любую из предпосылок можно формулировать в виде двух синтаксически несовместных утверждений. Эти утверждения в разных теориях (но не в одной теории) могут быть оба истинны. Одно из такого рода утверждений будем называть тезисом (Т), а другое – антитезисом (АТ). Рассмотрим нижеследующие идеализации теорий механики:
Т1. Движущийся объект является классическим объектом (нульмерным, имеющим траекторию движения).
АТ1. Движущийся объект является квантовым объектом (имеющим измерения, не имеющим траектории движения).
Т2. Измерение происходит только в инерциальных системах отсчета.
АТ2. Измерение происходит не только в инерциальных системах отсчета.
Т3. Скорость распространения физических взаимодействий (в том числе скорость света) неограниченна (бесконечна).
АТ3. Скорость распространения физических взаимодействий (в том числе скорость света) ограничена (не превышает с).
Т4. Прибор (измеряющий сигнал) не влияет на измеряемый объект.
АТ4. Прибор влияет на измеряемый объект.
Т5. Возможно с одинаковой определенностью одновременно измерить попарно любые свойства объекта.
АТ5. Невозможно одновременно измерить с одинаковой определенностью любые свойства объекта (канонически сопряженные - нельзя).
Можно показать, что ньютонова механика принимает предпосылки Т1, Т2, Т3, Т4, Т5, так как ее законы истинны именно на системе классических объектов при условии, что величины (пространство, время, масса, сила и т.п.), о которых утверждается в законах, измеряются только в инерциальных системах отсчета и при условиях, выраженных в других принимаемых ею тезисах. Нетрудно видеть, что эти тезисы очень сильно идеализируют объективно существующее механическое движение. Так, например, в природе нет объектов, вообще не имеющих измерений (классических объектов). Нет систем измерения (отсчета), на которые не действовали бы никакие силы (инерциальных систем измерения). Нет бесконечно больших скоростей. Нет объектов, никак не зависимых от влияния измеряющего сигнала (прибора).
Отсюда следует, что законы ньютоновой механики истинны в области теоретических объектов и эта истинность аналитическая, ибо теоретические объекты материально не существуют, а поэтому эмпирическими методами (наблюдения, измерения, материального эксперимента) нельзя проверить присущность или не присущность этим объектам каких-либо свойств или отношений. Аналитическую истинность можно установить только аналитическим методом, о котором мы уже говорили в главе III. Ясно, что эта истинность устанавливается в области интерпретации предмета ньютоновой механики, называемом ее физической реальностью.
Однако ньютонова механика приложима для решения задач, относящихся к определенной области объективно существующего механического движения. Эта область представляет опосредованный предмет ньютоновой механики. Относительно данной области ньютонова механика уже эмпирически истинна. Возникает вопрос, какова та область механического движения, которая является опосредованным предметом ньютоновой механики? Это может быть и нединамическое и динамическое движение.
Для ответа на поставленный вопрос опять-таки необходим анализ идеализаций Т1, …, Т5 этой теории. Предпосылки ньютоновой механики показывают, что классический объект больше всего подходит для описания нединамического и динамического движения макрообъектов. И если речь идет о динамическом движении макрообъектов, то описание будет асимптотическим и тем точнее, чем медленнее движение, т.е. чем более его скорость приближается к нулевой. В области нединамического движения истинность этой теории будет адекватной во всем диапазоне скоростей от 0 до ¥.
Релятивистская механика своим непосредственным предметом имеет физическую реальность, представляющую систему теоретических объектов, основанных на предпосылках Т1, Т2, АТ3, Т4, Т5. Существенное отличие от предпосылок ньютоновой механики состоит в том, что принимается в расчет то обстоятельство, что скорость распространения физических взаимодействий не бесконечна, а ограниченна. Ясно, что ньютонова и релятивистская механики в таком случае несовместимы (так как АТ3 несовместим с Т3). Но релятивистская механика также является аналитически истинной на системе уже иного рода объектов, основанных на только что указанных для нее идеализациях. А так как она применима для решения научно-практических задач, то истинна и эмпирически, но уже адекватно истинна на области динамического движения, не только близкой к нулевой, а во всем диапазоне скоростей от 0 до С. Асимптотически истинной она будет в области нединамического движения при скоростях приближающихся к 0.
Квантовая механика (точнее нерелятивистская квантовая механика) огрубляет и идеализирует механическое движение совершенно по-иному, чем классическая механика (ньютонова и релятивистская). Это видно из принимаемых ею идеализаций, выражаемых тезисами и антитезисами АТ1, Т2, Т3, АТ4, АТ5. Как видно, квантовая механика синтаксически несовместна и с ньютоновой механикой (так как антитезисы АТ1, АТ4 и АТ5 несовместны с Т1, Т4, Т5), и с релятивистской механикой (так как АТ1, Т3, АТ5 несовместны с Т1, АТ3, Т5).
Законы квантовой механики истинны на специфической системе теоретических объектов (вероятностных величин), представляющей квантово-механическую физическую реальность (ее непосредственный предмет). Поэтому истинность квантовой механики в области этого рода реальности, хотя и является аналитической, но существенно отличной от аналитической истинности (в области динамических величин) теорий классической механики.
Так как квантовая механика приложима для решения определенных прикладных задач, то она также и эмпирически истинна в области материального опосредованного предмета – объективной действительности специфического рода (механического движения квантовых объектов).
Метод гносеологического анализа теорий показывает таким образом, что он необходим для правильного применения методов установления истинности законов теорий. Действительно, чтобы правильно применить эти методы, надо прежде всего знать, относительно какого предмета теории устанавливается истинность. Если относительно непосредственного предмета, то истинность будет аналитической и методы ее установления надо применять аналитические. Если истинность устанавливается относительно опосредованного предмета, то она будет эмпирической и соответственно для ее установления надо применять эмпирические методы, и в первую очередь – прикладной (аппликативный) метод, метод решения прикладных задач.
Метод гносеологического анализа необходим также для решения проблемы сравнения теорий (§4, главы III). Дело в том, что сравнение теорий «в целом» показало свою полную бесперспективность. Теория представляет множество систем. Для решения проблемы сравнения теорий (проблемы " соизмеримости") существенно то, что теории представляют семиотические и гносеологические системы. Эти системы можно рассматривать в " чистом" виде. В первом случае рассмотрение теорий производится только в сфере языковых систем. Во втором случае теория рассматривается в сфере отношения языковой системы к чему-то внешнему по отношению к ней (ее опосредованному или непосредственному предмету, т.е. к области ее применимости или интерпретации). В обоих случаях происходит отвлечение от несущественных для данных целей аспектов теории и сравнение их по существенным для этих целей аспектам.
В общем виде метод гносеологического подхода к сравнению теорий будет следующим:
Уточнить, какого рода системы представляют сравниваемые теории, т.е. с точностью до каких идеализаций они рассматриваются.
Выяснить существенный аспект сравнения, т.е. установить тот конкретный род систем, по которым теории необходимо сравнивать в целях решения поставленной задачи.
Установить, сравнимы ли теории по выбранному аспекту. И если да, то найти результат этого сравнения. Для пояснения используем уже упоминавшийся по несколько иному поводу пример сравнения ньютоновой и релятивистской механик.
Эти механики являются и семиотическими, и гносеологическими системами. Последнее означает, что они являются языковыми системами, имеющими приложения в объективной действительности. Как языковые системы они представляют и синтаксические, и семантические системы. При этом в качестве семантических систем они являются и математическими и физическими системами, так как имеют и математическую, и физическую интерпретации (семантики).
Задачи, которые требуют сравнения теорий, могут быть самые различные. Допустим, нам надо проверить, соотносится ли релятивистская механика с ньютоновой по принципу соответствия Бора. Согласно условиям применения этого принципа существенно, чтобы обе теории могли быть представлены как семантические системы, имеющие математическую семантику (математические аппараты) в отвлечении от их физической семантики. Соответствие будет иметь место в том случае, когда математический аппарат любого закона релятивистской механики путем логической операции конкретизации можно будет свести к математическому аппарату некоторого закона ньютоновой механики. Но так как операция конкретизации является обратной по отношению к операции обобщения, то можно наличие соответствия показать путем обобщения математического аппарата закона ньютоновой механики в математический аппарат закона релятивистской механики. Этим приемом мы будем пользоваться.
Как математические системы, т.е. по математическим аппаратам, релятивистская и ньютонова механики, во-первых, сравнимы, так как рассматриваются с точностью до одних и тех же (математических) идеализаций, присущих теории действительных чисел. Во-вторых, они соотносятся как частная теория к общей.
Это можно показать, взяв математические аппараты законов ньютоновой механики, обобщив их и получив тем самым математические аппараты законов релятивистской механики. Например, возьмем закон ньютоновой механики  , где
, где 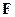 - сила,
- сила, 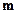 - масса,
- масса, 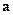 - ускорение. Рассмотрим этот закон с точностью до математической семантики, т.е. отвлечемся от его физической семантики. Тогда получим математический аппарат физического закон
- ускорение. Рассмотрим этот закон с точностью до математической семантики, т.е. отвлечемся от его физической семантики. Тогда получим математический аппарат физического закон  , где
, где 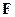 ,
, 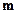 ,
, 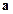 будут переменными для действительных чисел, и только. Сделаем ничего по существу не меняющие преобразования:
будут переменными для действительных чисел, и только. Сделаем ничего по существу не меняющие преобразования: 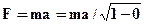 . Заметим, что 0 есть частное значение переменной
. Заметим, что 0 есть частное значение переменной 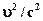 , где
, где 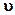 - переменная для чисел,
- переменная для чисел, 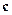 - число 300000. А теперь сделаем обобщение формулы
- число 300000. А теперь сделаем обобщение формулы 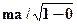 , поставив вместо 0 переменную
, поставив вместо 0 переменную 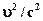 . Тогда получим математический аппарат закона релятивистской механики
. Тогда получим математический аппарат закона релятивистской механики 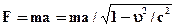 . Результат сравнения законен, так как семантика терминов
. Результат сравнения законен, так как семантика терминов 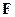 ,
, 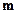 ,
, 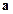 ,
, 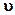 ,
, 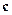 в частной и общей формулах одинаковы. После обобщения надо полученной математической формуле придать релятивистскую интерпретацию. В этой интерпретации переменные
в частной и общей формулах одинаковы. После обобщения надо полученной математической формуле придать релятивистскую интерпретацию. В этой интерпретации переменные 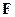 ,
, 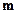 ,
, 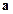 ,
, 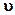 будут соответственно релятивистскими силой, массой, ускорением, скоростью, существенно отличными от соответствующих ньютоновских величин. Отличными хотя бы тем, что в релятивистской механике эти величины относительны, в то время как в ньютоновой механике они абсолютны. Символ
будут соответственно релятивистскими силой, массой, ускорением, скоростью, существенно отличными от соответствующих ньютоновских величин. Отличными хотя бы тем, что в релятивистской механике эти величины относительны, в то время как в ньютоновой механике они абсолютны. Символ 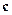 будет уже не просто означать число 300000, а скорость 300000 км/сек. В результате релятивистской интерпретации математическая формула
будет уже не просто означать число 300000, а скорость 300000 км/сек. В результате релятивистской интерпретации математическая формула 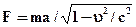 станет законом релятивистской механики.
станет законом релятивистской механики.
Пусть теперь перед нами поставлена другая задача: нам требуется сравнить результаты вычислений длины ракеты в полете и решить, какая из теорий более точно позволяет это сделать. Суть задачи говорит о том, что тут сравниваются теории как гносеологические системы, которые требуется сопоставить по адекватности отображения материального свойства иметь длину.
Допустим, длину ракеты измеряли на земле и получили результат 100 м. Но задача состоит в том, чтобы измерить ее в полете, т.е. в процессе динамического движения.
Представим себе, что ракета фотонная и летит со скоростью 270000 км/сек. Ясно, что измерить длину ракеты с Земли можно только при помощи лучей света. Выше мы уже говорили, что ньютонова механика принимает скорость света за бесконечную. Тогда в соответствии с законами преобразования координат в различных системах отсчета будет справедливым, что длина ракеты на Земле / ℓ 0 /и в полете /ℓ / одна и та же, т.е. ℓ = ℓ 0. Так как ℓ 0 = 100 м, то и ℓ =100 м.
 Однако релятивистская механика такую идеализацию скорости света не принимает и считает в соответствии с экспериментальными данными, что скорость света в вакууме равна 300000 км/сек. Тогда преобразования координат необходимо производить по законам Лоренца. В этом случае, если длина ракеты на Земле /ℓ 0/ была 100 м., то в движении она будет уже не ℓ 0, а ℓ 0 √ 1-
Однако релятивистская механика такую идеализацию скорости света не принимает и считает в соответствии с экспериментальными данными, что скорость света в вакууме равна 300000 км/сек. Тогда преобразования координат необходимо производить по законам Лоренца. В этом случае, если длина ракеты на Земле /ℓ 0/ была 100 м., то в движении она будет уже не ℓ 0, а ℓ 0 √ 1- 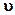 2 / c2. Если
2 / c2. Если 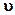 =270000 км/сек, а ℓ 0 =100 м, то измерение ракеты лучом света в полете покажет уже не 100 м, а только 50 м.
=270000 км/сек, а ℓ 0 =100 м, то измерение ракеты лучом света в полете покажет уже не 100 м, а только 50 м.
Какая же теория точнее, т.е. по законам какой теории надо измерять с земли длину ракеты в полете? Ответ ясен: если скорость приближается к c, то по законам релятивистской механики, так как скорость луча света не бесконечна, а конечна и реальное измерение не может быть осуществлено лучами света с бесконечной скоростью, ибо таковых в природе не существует. Так что в данном случае сравнение теорий по адекватности измерений, т.е. гносеологическому аспекту, приводит к выводу о большей адекватности релятивистской механики. Поэтому истинность утверждения о длине ракеты в релятивистской механике будет адекватной, а в ньютоновой - асимптотической.
Иного рода задачи могут потребовать сравнения теорий по иным аспектам, например, их сравнения как синтаксических систем или как семантических систем с физической семантикой и т.д. Во всех случаях сравнения теорий требуется метод их гносеологического анализа для выявления идеализаций, с точностью до которых рассматриваются сравниваемые теории. Последнее только и позволяет выделить аспекты сравнения. Вообще говоря, выявление идеализаций требуется для решения очень многих методологических и гносеологических проблем содержательных теорий.