Динамическое торможение с возбуждением от источника постоянного тока

Такое торможение осуществляется путем отключения обмотки статора от сети переменного тока и подключения ее к источнику постоянного тока, например, по одной из представленных на рис. 3.6. схем.

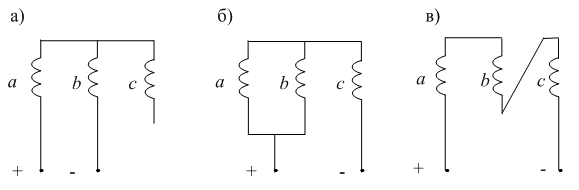
Рис. 3.6. Схемы подключения обмотки статора к источнику постоянного тока

Если обмотку статора подключить к источнику постоянного тока, то в воздушном зазоре двигателя образуется синусоидальное распределенное по расточке статора и неподвижное в пространстве электромагнитное поле. При вращении ротора проводники его обмотки будут пересекать неподвижное поле статора, и в них будет наводиться э.д.с. Под действием этой э.д.с. по обмотке ротора потечет ток, который образует также неподвижное в пространстве поле ротора. В результате взаимодействия неподвижных полей ротора и статора возникает тормозной момент.

Для того чтобы получить уравнения электромеханических характеристик двигателя в режиме динамического торможения, выраженные через те же параметры что и для двигательного режима, от реальной физической модели, которую мы представили выше, переходят к виртуальной модели, которую опишем. Первое предположение – двигатель питается не от источника постоянного тока, а от трехфазного источника переменного тока, обеспечивающего некоторый эквивалентный ток, создающий ту же м.д.с., что и реальный источник постоянного тока. Эквивалентный ток определяется из следующих соображений.

Амплитуда м.д.с., создаваемая переменным током, определяется соотношением

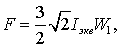
где w ₁ – число витков фазы статора. М.д.с. статорной обмотки, подключенной к источнику постоянного тока, например по схеме рис. 3.6.а, определяется соотношением:

Из условия равенства м.д.с. в обоих случаях, найдем

Так как переменный ток в статоре виртуальной модели создает вращающееся поле, а в реальном двигателе оно неподвижно, будем считать, что статор модели вращается навстречу полю с той же скоростью – поэтому его поле неподвижно в пространстве. Если проследить за процессом разгона статора против поля, то можно понять, что модель переходит на генераторный участок механической характеристики, см. рис. 3.4, в режим рекуперативного торможения.

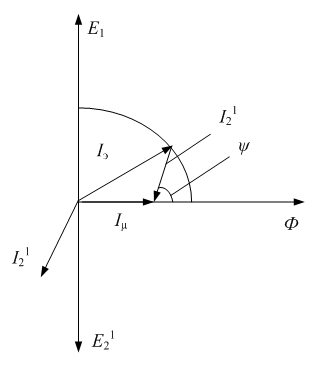
Рис. 3.7. Векторная диаграмма двигателя в режиме динамического торможения

Принимая во внимание что статорная обмотка подключена к источнику тока, векторная диаграмма двигателя имеет вид рис. 3.7, где обозначено E ₁, E ₂ ' – соответственно векторы э.д.с. статора и приведенной обмотки ротора. Ток намагничивания I _μ определяется геометрической суммой векторов приведенного вторичного – I ₂ ' и эквивалентного тока I _э. С понижением скорости ротора уменьшается вторичный ток и его фазовый сдвиг относительно э.д.с. E ₂ '. Напомним, что при этом модуль вектора эквивалентного тока постоянен. Поэтому при уменьшении скорости конец вектора тока I _э будет перемещаться по окружности по часовой стрелке и при заторможенном роторе совпадет с вектором I _μ . Следовательно, на малых скоростях двигатель оказывается сильно насыщен, а при больших – нет. Из векторной диаграммы имеем

(3.16)

I _э²=(I ₂ ')²+2 I _μ I ₂ ' sinΨ ₂+(I _μ )²;

(3.17)

где E ₂₀ ' – приведенная вторичная э.д.с. при синхронной скорости двигателя и намагничивающем токе I _μ , которая может быть найдена по кривой намагничивания двигателя, s =ω /ω ₀ – скольжение при динамическом торможении.

Решая совместно (3.16) и (3.17), находим

(3.18)

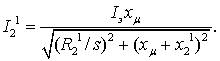
Механическая характеристика запишется выражением, аналогичным по структуре механической характеристике для двигательного режима,

(3.19)

M (s)=2 M _кт/(s / s _кт+ s _кт/ s),

где

(3.20)

M _кт=3 I _э² x _μ ²/(2ω ₀(x _μ − x ₂ '))

момент критический в режиме динамического торможения,

(3.21)

s _кт= R ₂ ' /(x ₁+ x ₂ ')

критическое скольжение в режиме динамического торможения.

Общий вид характеристик представлен на рис. 3.8.

Рис. 3.8. Механическая характеристика асинхронного двигателя
в режиме динамического торможения

Выражения (3.18), (3.19) показывают, что нам удалось выразить электромеханические характеристики в режиме динамического торможения при возбуждении двигателя постоянным током через те же параметры, что и в двигательном режиме при питании от сети переменного тока – (3.7), (3.13).