
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы регулирования момента и скорости
|
|
Рассматривая искусственные характеристики двигателей рис. 3.5, мы отметили, что их вид зависит от таких параметров, как активное сопротивление в цепи ротора, напряжение питания, индуктивное сопротивление в цепи статора, число пар полюсов и частота питающего напряжения.
Регулирование момента, как можно понять из анализа схемы замещения рис. 3.3, может быть осуществлено путем изменения напряжения. Например, с помощью тиристорного преобразователя или импульсным методом. При этом момент оказывается пропорционален квадрату напряжения, а регулирование возможно только вниз от номинального значения.
Регулирование скорости может быть осуществлено путем изменения активного сопротивления в цепи статора, изменением числа пар полюсов двигателя и регулированием частоты. Недостатком регулирования изменением активного сопротивления является то, что регулирование скорости осуществляется за счет изменения скольжения, а как следует из (3.8), электромагнитный к.п.д. двигателя определяется соотношением
(3.27)
η э= P / P э=ω /ω 0=1– s.
Следовательно, при уменьшении скорости уменьшается и электромагнитный к.п.д. Способ регулирования скорости числом пар полюсов лишен этого недостатка, так как он основан на изменении синхронной скорости при незначительном изменении скольжения. Недостатком такого способа является высокая дискретность регулирования и сложность обеспечения низких скоростей вращения. Всех перечисленных недостатков лишен частотный способ регулирования. Действительно, здесь регулирование осуществляется за счет изменения синхронной скорости при незначительном изменении скольжения, обеспечивающего высокое значение электромагнитного к.п.д. Причем скорость может регулироваться как вверх от номинальной, так и вниз. При использовании обратных связей частотное регулирование может обеспечить достаточно широкий диапазон регулирования скорости.
Можно отметить, что частотное регулирование является предпочтительным во всех отношениях для асинхронного двигателя, как при регулировании скорости, так и при регулировании момента и в этом отношении эквивалентно якорному управлению для двигателя постоянного тока независимого возбуждения, поэтому его мы рассмотрим подробнее.
Возможность частотного регулирования следует непосредственно из соотношения, определяющего синхронную скорость:
ω 0=2π f 1/ p.
Э.д.с. обмотки статора также пропорциональна частоте:
E 1= K Φ f 1.
Если пренебречь падением напряжения на обмотке статора, можно считать U ф≈ E 1. Отсюда
(3.28)
U ф≈ K Φ f 1.
Из этого выражения следует, что при неизменном напряжении и переменной частоте изменяется и поток двигателя. Уменьшение частоты ведет к увеличению потока и как следствие к насыщению машины, т.е. ухудшению энергетических показателей двигателя. Увеличение частоты ведет к снижению потока, т.е. к уменьшению момента и снижению перегрузочной способности двигателя. Решение очевидно – одновременно с частотой необходимо менять и напряжение.
При выборе соотношения между частотой и напряжением чаще всего исходят из условия сохранения постоянной перегрузочной способности двигателя, под которой понимают соотношениеλ = M к/ M с. Из уравнения (3.12), пренебрегая падением напряжения на обмотке статора и учитывая, что и x к∼ f 1 и ω 0∼ f 1, можно записать:
M к= A × U ф2/ f 12,
где A – коэффициент, независящий от напряжения и частоты. Тогда для любой частоты f 1 j и соответствующей ей скорости ω j можно записать:
λ (f 1 j)= M к j / M с(ω j)= A × U ф j 2/ f 1 j 2/ M с(ω j)=const,
где M с(ω j) – статический момент на валу двигателя при скорости ω j =2π f 1 j / p.
Из последнего выражения следует, что для любых двух значений частоты f 1 j и f 1 k должно выполняться условие
U ф j 2/ f 1 j 2/ M с(ω j)= U ф k 2/ f 1 k 2/ M с(ω k).
Отсюда следует основной закон изменения напряжения при частотном регулировании двигателя:
(3.29)

Принимая один из режимов, в частности (k), номинальным, т.е. полагая f 1 k = f 1н и U ф k = U фн, запишем основной закон изменения напряжения в относительных единицах:
(3.30)
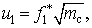
где u 1= U ф/ U фн, f 1*= f 1/ f 1н, m с= M с/ M сн.
Выражения (3.29) и (3.30) показывают, что напряжение должно меняться не только в функции частоты, но и в функции момента, который, в свою очередь, также может меняться при изменении скорости, например, в соответствии с выражением (1.3). Разделив обе части этого выражения на номинальный момент, мы получим общее выражение для зависимости относительного момента от скорости
m с= m 0+(1– m 0)(ω *) s,
где ω *=ω /ω н – относительная скорость. Подставляя полученное значение m с в уравнение (3.30), мы получим общий закон изменения напряжения от частоты при регулировании скорости:
при постоянном моменте на валу (s =0)
(3.31.а)
u 1=(f 1*)1,
при постоянной мощности (s =− 1)
(3.31.б)
u 1=(f 1*)1/2,
при вентиляторной нагрузке (s =2)
(3.31.в)
u 1=(f 1*)2.
Следует отметить, что полученные выражения в результате пренебрежения падением напряжения на обмотке статора являются приближенными. Однако их достаточно для того, чтобы иметь общее представление о закономерностях частотного регулирования асинхронных двигателей.