
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры обработки результатов измерений
|
|
Пример 1. Определение объема цилиндра с помощью штангенциркуля.
Предваряющий измерения анализ систематических погрешностей проведен в разд. 5. Измерение диаметра D и высоты h цилиндра проведем в разных местах и различных положениях цилиндра. Результаты измерений и вычислений занесем в табл. 2 и 3, где Δ Di=Dcp-Di и Δ hi=hcp-hi – разности между средним и измеренным значением.
Таблица 2
| № | Di, мм | Δ D i , мм | Δ Di2, мм2 | 
| Р и t |
| 21, 2 | 0, 1 | 0, 01 | 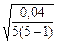 =
=0, 045 =
=0, 045
| P=0, 95 t=2, 8 | |
| 21, 4 | 0, 1 | 0, 01 | |||
| 21, 3 | 0, 0 | 0, 00 | |||
| 21, 2 | 0, 1 | 0, 01 | |||
| 21, 4 | 0, 1 | 0, 01 | |||
| Dср =21, 3 | Δ Dпр =0, 1 мм | Δ Dcл =0, 13 мм |
D =(21, 3 + 0, 16) мм
ε =0, 7% (9.1)
Р =0, 95
где абсолютная погрешность Δ D =0, 16 мм определяется соотношением 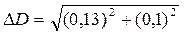 .
.
Таблица 3
| № | hi, мм | Δ hi, мм | (Δ hi)2, мм2 | 
| Р и t |
| 62, 1 | 0, 1 | 0, 01 | 0, 065 | P=0, 95 t=2, 8 | |
| 62, 3 | 0, 2 | 0, 04 | |||
| 62, 1 | 0, 0 | 0, 00 | |||
| 61, 9 | 0, 2 | 0, 04 | |||
| 62, 1 | 0, 0 | 0, 00 | |||
| hср =62, 1мм | Δ hпр =0, 1 мм | Δ hсл =0, 18 мм |
h =(62.1 + 0, 21) мм
ε =0, 34% (9.2)
Р =0, 95
Вычисляем среднее значение объема цилиндра:
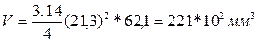 (9.3)
(9.3)
и относительную погрешность (см. формулу 3.13):
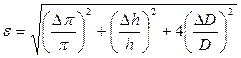 ; (9.4)
; (9.4)
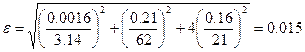 . (9.5)
. (9.5)
Первые два слагаемых подкоренного выражения меньше последнего более чем в 5 раз. Ими при вычислении можно пренебречь. Вычисляем абсолютную погрешность объема:
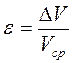 →
→ 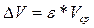 ; (9.6)
; (9.6)
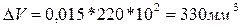 . (9.7)
. (9.7)
Записываем окончательный результат:
V =(221 + 3, 3)*102 мм3;
ε =1, 5%; (9.8)
Р =0, 95.
Убедимся в достоверности полученного значения объема цилиндра. Для этого его погрузим в мензурку с водой. Увеличение «объема воды» составило 22 мл, что в пределах погрешности измерений соответствует рассчитанному значению объема цилиндра.
Пример 2. Определение индуктивности катушки.
Индуктивность катушки определим из соотношения
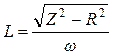 , (9.9)
, (9.9)
где Z – полное сопротивление катушки;
R – ее омическое сопротивление;
ω – циклическая частота переменного тока.
Полное сопротивление Z определим из закона Ома Iэф=Uэф/Z. (9.10)
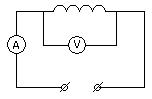 Проведем измерения силы тока Iэф в электрической цепи (рис. 6) при различных напряжениях.
Проведем измерения силы тока Iэф в электрической цепи (рис. 6) при различных напряжениях.
Результаты измерений и вычислений внесем в таблицу. Отметим полное сопротивление Z – косвенное измерение II класса
Рис. 6 Таблица 4
| № | Uэф, В | Iэф, А | Zi, Ом | Δ Zi | Δ Zi2 | Р и t |
| 0, 58 | 0, 95 4, 3 | |||||
| 0, 70 | ||||||
| 0, 95 | 99, 0 | |||||
| Zср =101 | Δ Zсл =5, 2 |
Чтобы найти абсолютную погрешность Δ Z, необходимо рассчитать и Δ Zпр, т.е. вклад приборных погрешностей и Δ Z. Из (9.10) на основании правила I имеем, что
 . (9.11)
. (9.11)
Для вольтметра на 150 В класса точности 0, 5 Δ Unp= 0.005*150В=0, 75В, для амперметра на 1 А класса точности 1, 5 Δ Inp =0, 015*1А=0, 015А. Учтя это, можно записать:
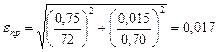 . (9.12)
. (9.12)
Отсюда
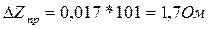 . (9.13)
. (9.13)
Так как 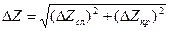 , (9.14)
, (9.14)
то в нашем случае
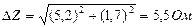 . (9.15)
. (9.15)
Таким образом, имеем
Z =(101 + 5, 5) Ом;
ε =5%; (9.16)
Р =0, 95.
R – определяем с помощью моста постоянного тока. Учитывая, что погрешность моста 0, 1%, окончательный результат можно записать в виде
R =(41, 4 + 0, 4) Ом;
ε =0, 10%; (9.17)
Р =0, 95.
Для сетевого переменного тока
ω =2π ν, (9.18)
где ν =(50 + 0, 1) Гц.
Зная R, Z, ω, легко рассчитать из уравнения (9.9) индуктивность L:
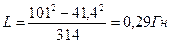 . (9.19)
. (9.19)
Для определения точности L выведем формулу относительной погрешности. В соответствии с правилом определения относительной погрешности (правило 1) из формулы (9.9) имеем:
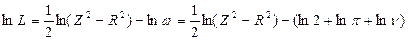 , (9.20)
, (9.20)
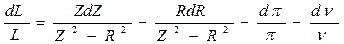 , (9.21)
, (9.21)
 . (9.22)
. (9.22)
Подставив значения, получим:
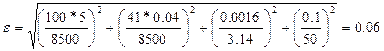 . (9.23)
. (9.23)
Легко заметить, что последними тремя членами подкоренного выражения можно пренебречь. Вычисление ε и Δ L производится устно. В результате наших измерений и вычислений мы получим, что
L =(0, 29 + 0, 018) Гн;
ε =6%; (9.24)
Р =0, 95.
Более детальный анализ методики измерений показывает, что мы допускаем систематическую погрешность при определении Z. В самом деле, мы определили Z как отношение показаний вольтметра Uэф к показаниям амперметра Iэф. Но из закона Ома
Z=Uэф/Iэф’, (9.25)
где Iэф’ – сила тока, идущего через катушку. Очевидно, что Iэф’ 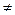 Iэф. Нетрудно показать, что если пренебречь индуктивным сопротивлением вольтметра в схеме (рис. 6), то
Iэф. Нетрудно показать, что если пренебречь индуктивным сопротивлением вольтметра в схеме (рис. 6), то
 , (9.26)
, (9.26)
где Iэф – показания амперметра;
Uэф – показания вольтметра;
RV – сопротивление вольтметра.
При RV → ¥ Z=Uэф/Iэф. В нашем примере для Uэф =94В, Iэф =0, 95А, Z =99, 2Ом. Сравнивая с данными табл. 4, видим, что систематическая погрешность Δ Zсист =0, 2 Ом. Эта систематическая погрешность значительно меньше случайной и ей можно пренебречь. Более того, взяв различные напряжения, мы эту систематическую погрешность частично обратили в случайную, частично учли.
Вставив в катушку сердечник, мы получили Iэф =0, 4А, Uэф =240В. Вольтметр стоял на пределе 300В, RV =40кОм. Если вычислить по формуле (9.9), получим Z =609Ом, т.е. погрешность первоначальной методики 9Ом или 1, 5%, что сравнимо с ошибкой величины Z (9.16). Следует помнить слова Менделеева Д. И. о том, что достойны внимания и обработки только те данные, где все влияния описаны, или, несомненно, приняты во внимание, т.е. вот почему, прежде чем измерять, необходимо тщательно проанализировать методику измерений, выявить и учесть систематические погрешности.
Для доказательства достоверности значений индуктивности катушки определите ее другим методом, например, с помощью моста Максвелла.
ЛИТЕРАТУРА
1. Агекян Т.А. Основы теории ошибок для астрономов и физиков.– 2-е изд. – М: Наука, 1972. –172с.
2. Касандрова О.Н, Лебедев В.В. Обработка результатов наблюдений. – М.: Наука, 1970. – 104с.
3. Зайдель А.Н. Ошибки измерений физических величин. –Л.: Наука, 1974. –108с.
4. Сквайрс Дж. Практическая физика/ Пер. с англ. под ред. Е.М. Лейкина. –М.: Мир, 1971. –246с.
5. Сурикова Е.И. Погрешности приборов и измерений. –Л.: Изд-во Ленингр. ун-та, 1975. –160с.
6. Румшинский Л.З. Математическая обработка результатов эксперимента. –М.: Наука, 1971. –192с.
7. Рабинович С.Г. Погрешности измерений. –Л.: Энергия, 1978. –262с.
8. Соловьев В.А., Яхонтова В.Е. Элементарные методы обработки результатов измерений. –Л.: Изд-во Ленингр. ун-та, 1977. –72с.
9. Кортнев А.В. и др. Практикум по физике. –М.: Высшая школа, 1963. –516с.
10. Лабораторный практикум по физике: Учебное пособие для студентов втузов./Под ред. А.С. Ахматова. –М.: Высшая школа, 1980. –360с.
СОДЕРЖАНИЕ.
1. Классификация измерений и их ошибок 1
2. Вероятность. Плотность вероятности. Доверительный
интервал и доверительная вероятность 2
3. Определение погрешности косвенных измерений 5
4. Приборы и их погрешности 9
5. Выявление, оценка и учет систематических погрешностей 14
6. Оценка истинного значения величины и достоверность
результатов измерений 17
7. Графики 18
8. Вычисления 20
9. Примеры обработки результатов измерений 21
Литература 26