Способы задания функции

1. Табличный.

При этом способе выписываются в определенном порядке значения аргумента 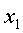, ,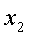..., 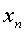и соответствующие значения функции

Таковы, например, таблицы тригонометрических функций, таблицы логарифмов и т. д. В результате экспериментального изучения явлений также могут получиться таблицы, выражающие функциональную зависимость между измеряемыми величинами. Так, например, в результате изме­рения температуры воздуха на метеорологической площадке в опре­деленный день получается следующая таблица:

Значение температуры Т (в градусах) в зависимости от времени t

(в часах)

Эта таблица определяет Т как функцию t.

2. Графический.

Если в прямоугольной системе координат на плоскости имеем некоторую совокупность точек М (х, у), при этом никакие две точки не лежат на одной прямой, параллельной оси Оу, то эта совокупность точек определяет некоторую однозначную функцию y = f(x); значениям аргумента являются абсциссы точек, значе­ниями функции — соответствующие координаты (рис.1).

Совокупность точек плоскости (хОу), аб­сциссы которых являются значениями неза­висимой переменной, а ординаты — соответ­ствующими значениями функции, называет­ся графиком данной функции.

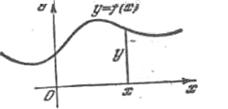
Рис.1

3. Аналитический

Сначала разъясним понятие «аналитическое выражение».

Аналитическим выражением будем называть символическое обозначение совокупности известных математических операций, которые производятся в определенной последовательности над числами и буквами, обозначающими постоянные или переменные величины. Отметим, что под совокупностью известных математических опе­раций будем понимать не только математические операции, извест­ные из курса средней школы (сложение, вычитание, извлечение корня и т. д.), но и те, которые будут определяться по мере изучения курса. Аналитическими выражениями, например, являются:

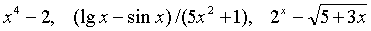
Если функциональная зависимость 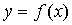такова, что f обозна­чает аналитическое выражение, то говорят, что функция у от x задана аналитически. Примеры функций, заданных аналитически: 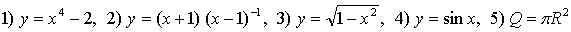и т. д. Здесь функции заданы аналитически с помощью одной формулы (под формулой понимается равенство двух аналитических выраже­ний).

Возрастание, убывание функции.

Если функция 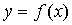такова, что большему значению аргумента соответствует большее значение функции, то функция 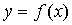называется возрастающей. Аналогичным обра­зом определяется убывающая функция.

Если функция 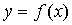такова, что большему значению аргумента соответствует меньшее значение функции, то функция 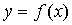называется убывающей.

Четность, нечЀ сть функции.

Функция называется четной, если для всех из области определения выполняется равенство: = . График четной функции симметричен относительно оси Оу.

Функция называется нечетной, если для всех из области определения выполняется равенство: = 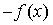. График нечетной функции симметричен относительно точки О(0; 0), т.е. относительно начала координат.

Замечание.

Иногда в определении понятия функции допу­скают, что каждому значению , принадлежащему некоторой области, соответствует не одно, а несколько значений или даже бесконеч­ное множество значений . В этом случае функцию называют мно­гозначной в отличие от определенной выше функции, которую назы­вают однозначной. В дальнейшем, говоря о функции, мы будем иметь в виду только однозначные функции. Если в силу необ­ходимости придется иногда иметь дело с многозначными функциями, то мы будем делать специальные оговорки.

Определим, далее, понятие элементарной функции.

Элементарной функцией называется функ­ция, которая может быть задана одной формулой вида у = f'(х), где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.

На основании определения следует, что элементарные функции являются функциями, заданными аналитическими.

Примеры элементарных функций: , ,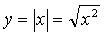

.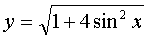