
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аддитивная мера
|
|
Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита:
I = l log h,
где I – количество информации, содержащейся в сообщении;
l – длина сообщения;
h – мощность исходного алфавита.
При исходном алфавите {0, 1}; l = 1; h = 2 и основании логарифма, равном 2, имеем
I = 1*log22 = 1.
Данная формула даёт аналитическое определение бита (BIT - BI nary digi T) по Хартли: это количество информации, которое содержится в двоичной цифре.
Единицей измерения информации в аддитивной мере является бит.
Пример 1. Рассчитать количество информации, которое содержится в шестнадцатеричном и двоичном представлении ASCII-кода для числа 1.
В соответствии с таблицей ASCII-кодов имеем: шестнадцатеричное представление числа 1 – 31, двоичное представление числа 1 – 00110001.
Тогда по формуле Хартли получаем:
для шестнадцатеричного представления I = 2log216 = 8 бит;
для двоичного представления I = 8 log22 = 8 бит.
Таким образом, разные представления ASCII-кода для одного символа содержат одинаковое количество информации, измеренной аддитивной мерой.
Статистический подход к измерению информации
В 30-х годах ХХ века американский ученый Клод Шеннон предложил связать количество информации, которое несет в себе некоторое сообщение, с вероятностью получения этого сообщения.
Вероятность p – количественная априорная (т.е. известная до проведения опыта) характеристика одного из исходов (событий) некоторого опыта. Измеряется в пределах от 0 до 1. Если заранее известны все исходы опыта, сумма их вероятностей равна 1, а сами исходы составляют полную группу событий. Если все исходы могут свершиться с одинаковой долей вероятности, они называются равновероятными.
Например, пусть опыт состоит в сдаче студентом экзамена по информатике. Очевидно, у этого опыта всего 4 исхода (по количеству возможных оценок, которые студент может получить на экзамене). Тогда эти исходы составляют полную группу событий, т.е. сумма их вероятностей равна 1. Если студент учился хорошо в течение семестра, значения вероятностей всех исходов могут быть такими:
p (5) = 0.5; p (4) = 0.3; p (3) = 0.1; p (2) = 0.1, где запись p (j) означает вероятность исхода, когда получена оценка j (j = {2, 3, 4, 5}).
Если студент учился плохо, можно заранее оценить возможные исходы сдачи экзамена, т.е. задать вероятности исходов, например, следующим образом:
p (5) = 0.1; p (4) = 0.2; p (3) = 0.4; p (2) = 0.3.
В обоих случаях выполняется условие:
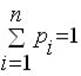
где n – число исходов опыта,
i – номер одного из исходов.
Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) - p i. Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле:
I = -log2 p i,
где p i – вероятность i-го сообщения (исхода).
Пример 1. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для студента-хорошиста.
Пусть I (j) – количество информации в сообщении о получении оценки j. В соответствии с формулой Шеннона имеем:
I (5) = -log2 0, 5 = 1,
I (4) = -log2 0, 3 = 1, 74,
I (3) = -log2 0, 1 = 3, 32,
I (2) = -log2 0, 1 = 3, 32.
Пример 2. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для нерадивого студента:
I (5) = -log2 0, 1 = 3, 32,
I (4) = -log2 0, 2 = 2, 32,
I (3) = -log2 0, 4 = 1, 32,
I (2) = -log2 0, 3 = 1, 74.
Таким образом, количество получаемой с сообщением информации тем больше, чем неожиданнее данное сообщение. Этот тезис использован при эффективном кодировании кодами переменной длины (т.е. имеющими разную геометрическую меру): исходные символы, имеющие большую частоту (или вероятность), имеют код меньшей длины, т.е. несут меньше информации в геометрической мере, и наоборот.
Формула Шеннона позволяет определять также размер двоичного эффективного кода, требуемого для представления того или иного сообщения, имеющего определенную вероятность появления.
Пример 3. Есть 4 сообщения: a, b, c, d с вероятностями, соответственно, р(a) = 0, 5; р(b) = 0, 25; р(c) = 0, 125; р(d) = 0, 125. Определить число двоичных разрядов, требуемых для кодирования каждого их четырех сообщений.
В соответствии с формулой Шеннона имеем:
I (a) = -log20, 5 = 2,
I (b) = -log20, 25 = 2,
I (c) = -log20, 125 = 3,
I (d) = -log20, 125 = 3.
Судя по примеру 1 из раздела эффективного кодирования, эффективное кодирование методом Шеннона-Фано сформировало для заданных сообщений (символов) коды полученной длины.
Пример 4. Определить размеры кодовых комбинаций для эффективного кодирования сообщений из примера 1.
Для вещественных значений объемов информации (что произошло в примере 1) в целях определения требуемого числа двоичных разрядов полученные значения округляются до целых по традиционным правилам арифметики. Тогда имеем требуемое число двоичных разрядов:
для сообщения об оценке 5 – 1,
для сообщения об оценке 4 – 2,
для сообщения об оценке 3 – 3,
для сообщения об оценке 2 – 3.
Проверим результат, построив эффективный код для сообщений об исходах экзамена методом Шеннона-Фано. Исходные данные – из примера 1. Имеем:
| Исходные символы | Вероятности | Коды |
| Сообщение об оценке 5 | 0, 5 | |
| Сообщение об оценке 4 | 0, 25 | |
| Сообщение об оценке 3 | 0, 125 | |
| Сообщение об оценке 2 | 0, 125 |
Таким образом, задача решена верно.
Помимо информационной оценки одного сообщения, Шеннон предложил количественную информационную оценку всех сообщений, которые можно получить по результатам проведения некоторого опыта. Так, среднее количество информации I ср, получаемой со всеми n сообщениями, определяется по формуле:
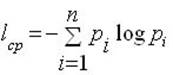
где pi – вероятность i-го сообщения.
Пример 5. Определить среднее количество информации, получаемое студентом-хорошистом, по всем результатам сдачи экзамена.
В соответствии с приведенной формулой имеем:
I ср = - (0, 5*log20, 5 + 0, 3*log20, 3 + 0, 1*log20, 1 + 0, 1*log20, 1) = 1, 67.
Пример 6. Определить среднее количество информации, получаемое нерадивым студентом, по всем результатам сдачи экзамена.
В соответствии с приведенной формулой имеем:
I ср = - (0, 1*log20, 1 + 0, 2*log20, 2 + 0, 4*log20, 4 + 0, 3*log20, 3) = 1, 73.
Большее количество информации, получаемое во втором случае, объясняется большей непредсказуемостью результатов: в самом деле, у хорошиста два исхода равновероятны.
Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. p 1 = p 2 = 0, 5. Тогда имеем в соответствии с формулой для расчета I ср:
I ср = -(0, 5*log20, 5 + 0, 5*log20, 5) = 1.
Эта формула есть аналитическое определение бита по Шеннону: это среднее количество информации, которое содержится в двух равновероятных исходах некоторого опыта, составляющих полную группу событий.
Единица измерения информации при статистическом подходе – бит.
На практике часто вместо вероятностей используются частоты исходов. Это возможно, если опыты проводились ранее и существует определенная статистика их исходов. Так, строго говоря, в построении эффективных кодов участвуют не частоты символов, а их вероятности.
Семантический подход к измерению информации
Учитывает целесообразность и полезность информации. Применяется при оценке эффективности получаемой информации и ее соответствия реальности.
В рамках этого подхода рассмотрим такие меры, как целесообразность, полезность (учитывают прагматику информации) и истинность информации (учитывает семантику информации).