Геометрическое определение

Ввиду соотношения 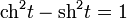гиперболические функции дают параметрическое представление гиперболы x ² − y ² = 1 (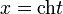, ). При этом аргумент t = 2 S, где S — площадь криволинейного треугольника OQR, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Свойства

Связь с тригонометрическими функциями

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

.

.

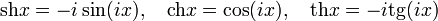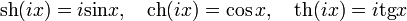Важные тождества

1. 
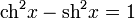
2. Чётность:
1. 
2. 
3. 
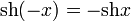
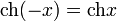
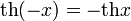
3. Формулы сложения:
1. 
2. 
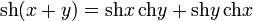
4. Формулы двойного угла:
1. 
2. 
3. 
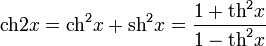
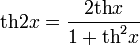
5. Формулы понижения степени
1. 
2. 

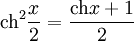
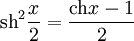
1. Производные:
1. 
2. 
3. 
4. 
5. 
6. 
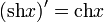
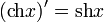
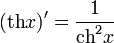
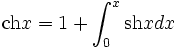
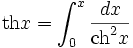
2. Интегралы:
1. 
2. 
3. 
4. 
5. 

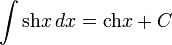
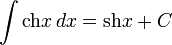
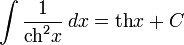
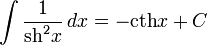
Разложение в степенные ряды

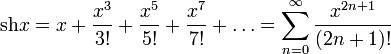
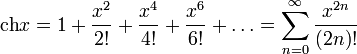
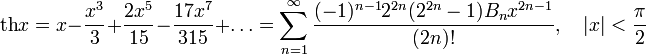
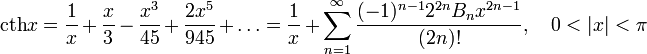(Ряд Лорана)

Здесь B_n — числа Бернулли.

Графики