
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Следствие из утверждений 11.11
|
|
и 11.12: Для того, чтобы прямую ли-нию из общего положения перевести в проецирующее, её необходимо прежде
вращением вокруг оси, перпендикуляр-
ной к одной плоскости проекций, пе-
ревести в положение линии уровня, а
затем, приняв это положение за исхо-
дное, вращением вокруг другой оси, перпендикулярной к другой плоскости проекций, перевести в искомое прое-цирующее положение.
11.2.2. Способ последовательного вращения вокруг двух проецирую-щих осей и решение метрических задач
1. Последовательное вращение отрезка АВ прямой общего положения вокруг двух взаимно-перпендикулярных осей и его графическая модель
Возможные варианты положения осей вращения і1 и і2 (рис.11.9, а - и):
Вариант а:
(і1 ^ П1)Î П2; (і2 ^ П2) Î П1; і1 х і2 = (А Î х12);
Вариант б:
(і1 ^ П1)Î П2; (і2 ^ П2) || П1;
Вариант в:
(і1 ^ П1) || П2; (і2 ^ П2)Î П1; і1 х і2 =(В Î П1);
Вариант г:
(і1 ^ П1) || П2; (і2 ^ П2)Î П1; і1 х і2 = С;
Вариант д:
(і1 ^ П1) || П2; (і2 ^ П2)Î П1; і1 ∸ і2;
Вариант е:
(і2 ^ П2) || П1; (і1 ^ П1)Î П2; і1 ∸ і2 ;
Вариант ж:
(і1 ^ П2) || П1; (і2 ^ П1)Î П2; і1 ∸ і2 ;
Вариант з:
(і1 ^ П1) || П2; (і2 ^ П2) || П1; і1 ∸ і2 ;
Вариант и:
(і2 ^ П2) || П1; (і1 ^ П1) || П2; і1 ∸ і2.
На выбор варианта расположения осей і1 и і2 влияют позиционные особен-ности исходного условия конкретной метрической задачи, что затем сказыва-ется на рациональности её графичес-кого решения.
Дано: а (а1, а2); і1 ^ П1; і2 ^ П2;
Требуется: 1. а ↷ а1 || П2;
2. а1 ↷ а2 ^ П1.
Решение (рис.11.10):
1. (О1 º і1) Î О1С1 ^ а1; С1 = О1С1 х а1;
2. О1С1 ↷ О1 С11 ^ х12; а1 ↷ а11 || х12;
а2 ® а12 = | a |; Ð j ° = | j °| а к П1.
3. ( О12 º і22 ) Î О12 112 ^ a12;
112 = O12112 х a12;

|
Рис. 11.11. Преобразование проекций
отрезка общего положения в его проекции в проецирующем
положении
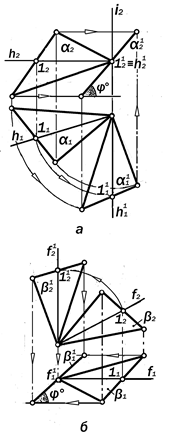
|
Рис.11.12. Преобразование проекций плоскости общего положения в её проекции проецирующего положения.
4. О12112 ↷ О22122 || х12; а12 ↷ а22 ^ х12 ;
a11 ® a21 - точка.
Если оси вращения проводить че-рез один из концов отрезка, то гра-фическое решение задачи упрощается
(рис. 11.6, 11.7).
ПРАВИЛО 4: Для того, чтобы пре-образовать ортогональные проекции прямой общего положения в проекции этой же прямой в том или ином про-ецирующем положении, необходимо и достаточно прежде преобразовать их в проекции линий уровня вращением вокруг первой оси, повернув радиус вращения отрезка до того или иного проецирующего положения, а затем, определив новый радиус вращения пря-мой в положении линии уровня, повер-нуть его вокруг второй оси до поло-жения, совпадающего с плоскостью уровня, проходящего через вторую ось вращения.
2. Вращение плоской фигуры вокруг одной оси (рис.11.12, а, б)
Классическим примером плоской фигуры является треугольник. В общем случае его стороны, как отрезки пере-секающихся прямых, занимают в прост-ранстве общее положение. Поэтому вращением вокруг одной проецирую-щей оси их невозможно привести в то или иное частное положение. Если же предположить, что одна сторона треу-гольника общего положения является его линией уровня, то, как следует из утверждения 11.12, её можно одним по-воротом вокруг проецирующей оси пе-ревести в положение, перпендикуляр-ное к тойплоскости проекций, по отно-шению к которой ось вращения парал-лельна. Тогда плоскость a треугольни-ка АВС, содержащая в себе перпенди-куляр к той или иной плоскости про-екций, также займёт то или иное прое-цирующее положение. При этом та или иная линия уровня этой плоскости при-обретает значение главного элементапреобразования её ортогональных про-екций.
Утверждение 11.12. Плоскую фигу-ра общего положения вращением во-круг той или иной проецирующей о си можно повернуть до того или иногопроецирующего положения если при-нять за основной элемент соответ-ствующего преобразования его орто-гональных проекций ту или иную её
линию уровня, которую одним поворо-том можно перевести в проецирую-щее положение.
Из этого утверждения вытекают два правила:
ПРАВИЛО 5: Для того, чтобы ор-тогональные проекции a1, a2 плоскос-ти a общего положения преобразо-вать в проекции этой же плоскости, но перпендикулярной к П2, необходимо и достаточно провести в ней горизон-таль h (h1, h2), выбрать ось і ^ П1 и по-вернуть вокруг неё a1 в конгруєнтную ей фигуру a11 таким образом, чтобы h1 заняла положение h11 ^ x12. Тогда h2 пре-образуется в точку h12, а a2 – в прямую a12, угол j° наклона которой к оси х12 метрически равен углу наклона пло-скости a к плоскости П1 (рис. 11.12, а).
ПРАВИЛО 6: Для того, чтобы ор-тогональные проекции b1, b2 плоскос-ти b общего положения преобразо-вать в проекции b11, b12 этой же плос-кости, но находящейся в горизонталь-но-проецирующем положении, необхо-димо и достаточно провести в ней фронталь f (f1, f2), выбрать ось враще-ния і ^ П2 и повернуть вокруг неё b2 в конгруэнтную ей фигуру b12 таким об-разом, чтобы f2 заняла положение f12 ^ x12. Тогда f 1 преобразуется в точку f 1, а b1- в прямую b11, угол j ° наклона ко-торой к оси х12 метрически равен углу наклона плоскости b к плоскости П2 (рис. 11.12, б).
3. Последовательное вращение плоской фигуры вокруг двух проециру-ющих осей и его графическая модель.
Дано 1. і1 ^ П1; і2 ^ П2; a (a1, a2);
(рис.11.13, а);
2. і1 ^ П2; і2 ^ П1; b (b1, b2);
(рис.11.13, б).
Требуется:
1.1. a ↷ a1 ^ П2; (і1 ^ П1);
1.2. a1 ↷ a2 ‖ П1; (і2 ^ П2);
2.1. b ↷ b1 ^ П1; (і1 ^ П2);
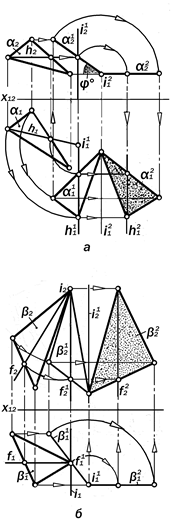
|
Рис. 11.13. Графическая модель
последовательного вращения плоской
фигуры вокруг двух проецирующих
осей
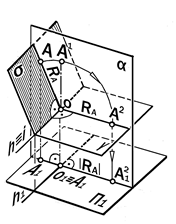
|
Рис11.14. Геометрическая модель процесса вращения точки, прямой и лоской фигуры вокруг линии уровня
2.2. b1 ↷ b2 ‖ П2; (і2 ^ П1).
Решение: (рис. 11.13, а):
1. h Î a; h2 ^ A2 A1; h1 É A1, 11;
2. i1 ^ П1; (і11 – точка; і12 ^ х12);
3. h1 ↷ h11 ‖ A1 A2; a1 ↷ a11 @ a1;
4. h2 ® h12 – в точку;
a2 ® a12 - в прямую;
Ð a21, x12 = | j° | Ð a, П1;
5. і2 ^ П2; (і22 – точка; і21 ^ х12);
6. a12 ↷ a22 ^ А1 А2;
7. a11 ® a21 @ | a | - истинный вид фигуры a, который содержит информа-цию о метрике её сторон, углов между ними, высот, площади и т.д.
Решение: (рис.11.13. б):
1. f Î b; f1 ^ A1 A2; f2 É A2, 12;
2. A Î i ^ П2 (і2 – точка, і11 ^ х12);
3. f2 ↷ f12 ‖ A1 A2; f1 ® f11 – точку;
b1 ® b11 - прямую;
4. і2^ П1 (і21 – точка; і22 ^ х12;
5. b11 ↷ b21 ^ А1 А2;
6. b12 ® b22 = | b | - искомый вид фигуры b, который содержит всю иско-мую информацию о его метрике.
ПРАВИЛО 7: Для того, чтобы пре-образовать ортогональные проекции плоской фигуры общего положения в проекции этой же фигуры, находящей-ся в том или ином положении уровня, необходимо и достаточно прежде изо-
бразить ту или иную её линию уровня, принять её за основной элемент пре-образования и, вращением вокруг пер-вой проецирующей оси, повернуть до проецирующего положения. В резуль-тате одна из проекций плоской фигу-ры выродится в наклонную прямую ли-нию, угол между которой и осью х12 ра-вен значению угла наклона её плоскос-ти к той или иной плоскости проек-ций. После этого следует выбрать вторую ось, параллельную новому по-ложению плоской фигуры и повернуть её вырожденную проекцию из наклон-ного положения в горизонтальное, что вызовет преобразование невыро-жденной проекции фигуры в первом по-ложении в новую проекцию, конгруэн-тную самой фигуре. Эта проекция является искомой, так как содержит
всю информацию о метрике этой фи-
гуры.