Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Производные высших порядков. Дифференциалы первого и высших порядков и их приложения.
|
|
Производной второго порядкаили второй производной функции у = f (х) называется производная от ее первой производной, т. Е. (у ')'. Обозначается вторая производная одним из следующих символов: у», f ''(х), 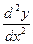 .
.
Если s = s (t) – закон прямолинейного движения материальной точки, то s '= 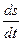 - скорость, а s»=
- скорость, а s»=  - ускорение этой точки.
- ускорение этой точки.
Если зависимость функции у от аргумента х задана в параметрическом виде уравнениями х = х(t), у=у(t), то:
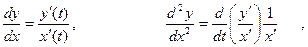 (3)
(3)
где штрих обозначает производную по t.
Производной n -го порядка функции у=t(х) называется производная от производной (n -1)-го порядка данной функции. Для n -й производной употребляются следующие обозначения: у(n), f (n) (х), 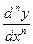 . Таким образом,
. Таким образом,
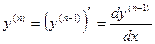 .
.
 Дифференциалом первого порядка функции у = f (x)называется главная, часть ее приращения, линейно зависящая от приращения
Дифференциалом первого порядка функции у = f (x)называется главная, часть ее приращения, линейно зависящая от приращения 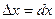 независимой переменной х. Дифференциал
независимой переменной х. Дифференциал 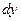 функции равен произведению ее производной и дифференциала независимой переменной
функции равен произведению ее производной и дифференциала независимой переменной 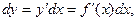 поэтому –справедливо равенство
поэтому –справедливо равенство 
Из рисунка видно, что если МN - дуга графика функции  МТ –касательная, проведенная к нему в точке М (х, у), и
МТ –касательная, проведенная к нему в точке М (х, у), и 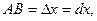 то CT = dy, а отрезок
то CT = dy, а отрезок  Дифференциал функции dy о
Дифференциал функции dy о  тличается от ее приращения
тличается от ее приращения  на бесконечно малую высшего порядка по сравнению с
на бесконечно малую высшего порядка по сравнению с 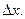
Непосредственно из определения дифференциала и правил нахождения производных имеем:
1) 


2)  если х – независимая переменная;
если х – независимая переменная;
3) 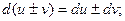
4) 
5) 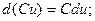
6) 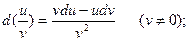

7) 
Дифференциалом n -го порядка функции у = f (х) называется дифференциал от дифференциала (n -1)-го порядка этой функции, т. Е. dny = d (dn -1 y).
Если дана функция у=f (х), где х – независимая переменная, то d2у= у»dх2, d3у=у'»dх3, …, dnу= y(n)dxn.
Если у=f (u), где u= 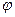 (x), то d2y=y//(du)2+y/d2u, где дифференцирование функции y выполняется по переменной и. (Это имеет место и для дифференциалов более высоких порядков.)
(x), то d2y=y//(du)2+y/d2u, где дифференцирование функции y выполняется по переменной и. (Это имеет место и для дифференциалов более высоких порядков.)
Так как дифференциал функции отличается от ее приращения на бесконечно малую величину высшего порядка по сравнению с величиной dх, то  или
или  , откуда
, откуда  .
.
Полученная формула часто применяется для приближенного вычисления значений функции при малом приращении 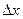 независимой переменной х.
независимой переменной х.
С помощью дифференциала функции вычисляют абсолютную погрешность функции 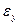 , если известна абсолютная погрешность
, если известна абсолютная погрешность  аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
Пусть требуется вычислить значение функции у = f (х) при некотором значении аргумента х, истинная величина которого нам неизвестна, но дано его приближенное значение x 0 с абсолютной погрешностью  : х= x 0+ dх,
: х= x 0+ dх, 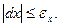 Тогда
Тогда

Отсюда видно, что 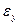 =
= 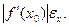 Относительная погрешность функции
Относительная погрешность функции  выражается формулой
выражается формулой
 =
= 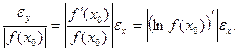
Литература: К.А. Хасеинов Каноны математики. Стр.167-184
Практическое занятие 7
Найти производные следующих функций.
1.  2.
2. 
3. 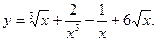 4.
4. 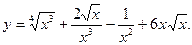
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 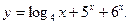
11. 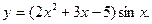 12.
12. 
168. 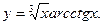 169.
169. 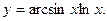
13.  14.
14. 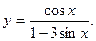
15.  16.
16. 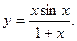
17 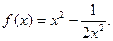 Найти
Найти 
18. 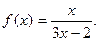 Найти
Найти 
19.  Найти
Найти  .
.
20. 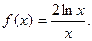 Найти
Найти 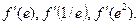
21. 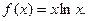 Найти
Найти 
22 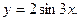 23.
23. 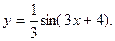
24. 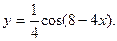 25.
25. 
26. 
27.  28.
28. 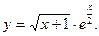
29.  30.
30. 
31.  32.
32. 
33. 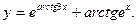 34
34 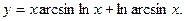
35. 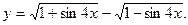 36.
36. 
37. 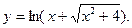 38.
38. 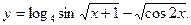
39. 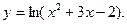 40.
40. 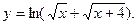
41. 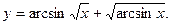 42.
42. 
43 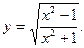 44.
44. 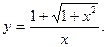
45.  46.
46. 
47. 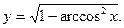 48.
48. 
49. 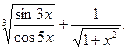 50.
50. 
51.  52.
52. 
53 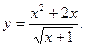 54.
54. 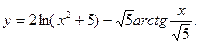
55.  56.
56. 
57. 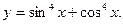 58.
58. 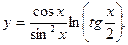
Для функций, заданных параметрически, найти 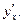
59. 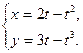 60.
60. 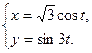
61. 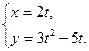 62.
62. 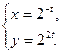
63. 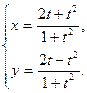 64.
64. 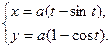
65.  66.
66. 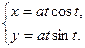
67.  68.
68. 
69.  70.
70. 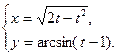
71. 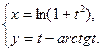 72.
72. 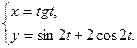
Найти  в указанных точках.
в указанных точках.
73. 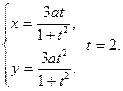 74.
74. 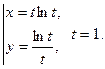
75. 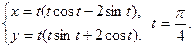 76.
76. 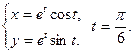
Найти  для следующих функций, заданных неявно.
для следующих функций, заданных неявно.
77.  78.
78. 
79. 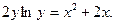 80.
80. 
81.  82.
82. 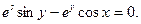
83. Найти  в точке (0; 1), если
в точке (0; 1), если 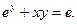
84. Найти значение  в точке х = 1, если
в точке х = 1, если 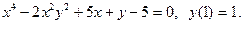
Найти дифференциалы следующих функций.
1. 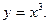 2.
2. 
3. 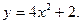 4.
4. 
5. 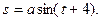 6.
6. 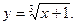
7. 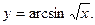 8.
8. 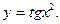
9. 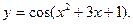 10.
10. 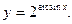
11. 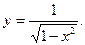 12.
12. 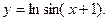
13. Вычислить приближенно:
а)  б)
б) 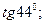 в)
в) 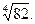 г)
г) 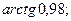
д) 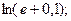 е)
е)  при х = 2, 01.
при х = 2, 01.
ж)  при х = 2, 9.
при х = 2, 9.
Найти производные второго порядка.
1. 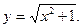 2.
2. 
3.  4.
4. 
5. 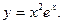 6.
6. 
7.  8.
8. 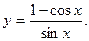
Найти производные указанного порядка от данных функций.
9.  10.
10. 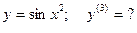
11. 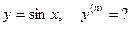 12.
12. 
Контрольная работа по теме «Производная и дифференциал»
Вариант 1
Найти производные:
1. 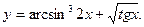 2.
2. 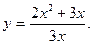
3.  4.
4. 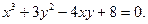
5. Найти частное значение производной от функции 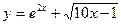 при х =1.
при х =1.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 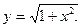
8. Найти вторую производную от функции 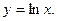
Вариант 2
Найти производные:
1. 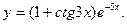 2.
2. 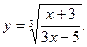
3.  4.
4. 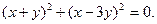
5. Найти частное значение производной от функции 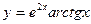 при х =1.
при х =1.
6. Написать уравнение касательной к кривой 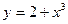 в точке с абсциссой
в точке с абсциссой
х =1.
7. Найти дифференциал функции 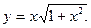
8. Найти вторую производную от функции 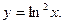
Вариант 3
Найти производные:
1. 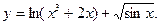 2.
2. 
3.  4.
4. 
5. Найти частное значение производной от функции  при х =
при х = 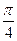 .
.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =2.
в точке с абсциссой х =2.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 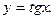
Вариант 4
Найти производные:
1. 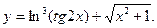 2.
2. 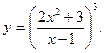
3. 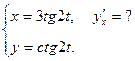 4.
4. 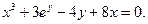
5. Найти частное значение производной от функции 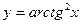 при х =1.
при х =1.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 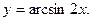
Вариант 5
Найти производные:
1.  2.
2. 
3.  4.
4. 
5. Найти частное значение производной от функции  при х =0.
при х =0.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 
Вариант 6
Найти производные:
1.  2.
2. 
3. 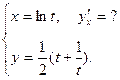 4.
4. 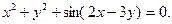
5. Найти частное значение производной от функции  при х =0.
при х =0.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =0.
в точке с абсциссой х =0.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 
Вариант 7
Найти производные:
1. 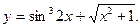 2.
2. 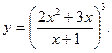
3. 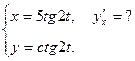 4.
4. 
5. Найти частное значение производной от функции 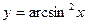 при х =1.
при х =1.
6. Написать уравнение касательной к кривой 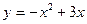 в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 
Вариант 8
Найти производные:
1.  2.
2. 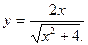
3.  4.
4. 
5. Найти частное значение производной от функции  при х =0.
при х =0.
6. Написать уравнение касательной к кривой  в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 
8. Найти вторую производную от функции 
Вариант 9
Найти производные:
1. 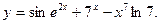 2.
2. 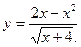
3.  4.
4. 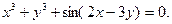
5. Найти частное значение производной от функции  при х =0.
при х =0.
6. Написать уравнение касательной к кривой 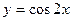 в точке с абсциссой х =0.
в точке с абсциссой х =0.
7. Найти дифференциал функции 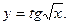
8. Найти вторую производную от функции 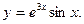
Вариант 10
Найти производные:
1.  2.
2. 
3. 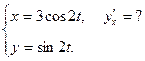 4.
4. 
5. Найти частное значение производной от функции  при х =1.
при х =1.
6. Написать уравнение касательной к кривой 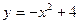 в точке с абсциссой х =1.
в точке с абсциссой х =1.
7. Найти дифференциал функции 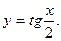
8. Найти вторую производную от функции