Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрицы и операции над ними.
|
|
Определение. Матрицей называется множество чисел, которое составляет прямоугольную таблицу, состоящее из m строк и n столбцов
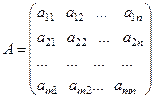
коротко матрицу обозначают так:
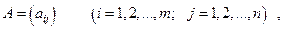
где 
элементы данной матрицы, i – номер строки, j – номер столбца.
Если в матрице число строк равно числу столбцов (m = n), то матрица называется квадратной n -го порядка, а в противном случае – прямоугольной.
Если m= 1 и n > 1, то получаем однострочную матрицу
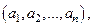
которая называется вектор-строкой, если, же m > 1 и n =1, то получаем одностолбцовую матрицу
,
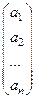которая называется вектор-столбцом.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой элементы главной диагонали равны единице, называется единично, обозначается E.
Матрица, полученная из данной заменой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается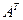 
.
Две матрицы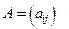 
и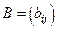 
равны, если равны между собой элементы, стоящие на одинаковых местах, то есть если
при всех i и j (при этом число строк (столбцов) матриц A и B должно быть одинаковым).
1°. Суммой двух матриц A =(aij) и B =(bij) с одинаковым количеством m строк и n столбцов называется матрица C =(cij), элементы которой определяются равенством
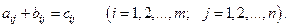
Сумму матриц обозначают C = A + B.
Пример.
.
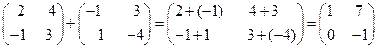20. Произведением матрицы A =(aij) на число λ называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы A на число λ:
λ A = λ (aij)=(λ aij), (i =1, 2…, m; j =1, 2…, n).
Пример.
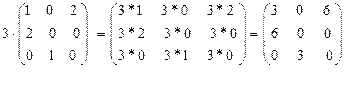
30. Произведением матрицы A =(aij), имеющей m строк и k столбцов, на матрицу B =(bij), имеющей k строк и n столбцов, называется матрица C =(cij), имеющая m строк и n столбцов, у которой элемент cij равен сумме произведений элементов i -ой строки матрицы A и j -го столбца матрицы B, то есть
При этом число столбцов матрицы A должно быть равно числу строк матрицы B. В противном случае произведение не определено. Произведение матриц обозначается A*B = C.
Пример.
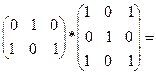
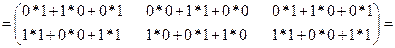
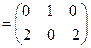
Для произведения матриц не выполняется равенство между матрицами A*B и B* A, в общем случае одна из них может быть не определена.
Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.
Пример. Пусть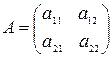 
, 
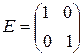, тогда согласно правилу умножения матриц имеем
=
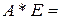
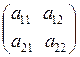
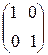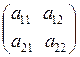
и
,
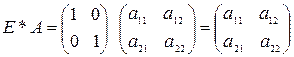откуда заключаем, что
и 