Определители.

Пусть дана квадратная матрица третьего порядка:

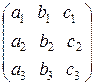(1)

Определение. Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом

и определяемое равенством

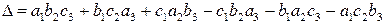.(2)

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «-», полезно использовать следующее правило треугольников.

«+» «-»

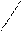
Пример.

Свойства определителей рассмотреть самостоятельно.

Определение. Матрица называется обратной квадратной матрице A, если .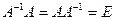

Определение. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.

Утверждение. Всякая невырожденная матрица имеет обратную.

Элементарными преобразованиями матриц являются:

1. перестановка местами двух параллельных рядов матрицы;

2. умножение всех элементов матрицы на число, отличное от нуля;

3. прибавление ко всем элементами ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Матрица В, полученная из матрицы А с помощью элементарных преобразований, называется эквивалентной матрицей.

Элемент строки матрицы называется крайним, если он отличен от нуля, а все элементы строки, находящиеся левее него, равны нулю. Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. Например:

- не ступенчатая; 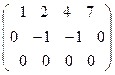- ступенчатая.