Односторонние пределы функции.

НЕДЕЛЯ 5

Лекция 9

Функция. Действительные числа. Предел функции.

Односторонние пределы функции.

Совокупность рациональных Q и иррациональных чисел образует множество действительных (вещественных) чисел R. Между множе­ством точек прямой и множеством R всегда можно установить взаимно однозначное соответствие. Если это соответствие установлено, то прямую называют числовой осью.Совокупность всех чисел х, удовле­творяющих условию а< х< b (а 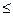х 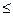b), называется интервалом (от­резком)и обозначается (a; b) ([а; b]).

Модулем (абсолютной величиной)действительного числа а назы­вают неотрицательное число |а|, определяемое условиями: 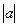=а, если а 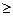0, и 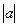= - а, если а < 0. Для любых действительных чисел а и b верно неравенство |а+ b| 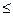|а|+| b|.

Числа, получающиеся в результате счета, называются натуральными. Множество натуральных чисел обозначается N. Множество натуральных чисел, множество целых отрицательных чисел и число 0 образуют множество целых чисел, которое обозначается Z.

Рациональным числом называется число, представимое в виде 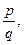где р – целое, а знаменатель q – натуральное число. Множество рациональных чисел обозначается Q.

Всякое число, не представимое в виде 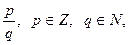называется иррациональным числом. Определение рациональных и иррациональных чисел можно дать в следующем виде: Числа, представимые в виде конечной десятичной или бесконечной десятичной периодической дробью называются рациональными числами. Числа, которые представляются бесконечными, но непериодическими десятичными дробями называются иррациональными числами.

Множество всех рациональных и иррациональных чисел называются множеством действительных (вещественных) чисел. Множество действительных чисел обозначается R,. R = {-¥, +¥ }

Абсолютной величиной или модулем действительного числа х, обозначаемого | x|, называется неотрицательное число, определяемое равенствами

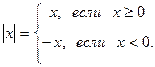
Свойства абсолютной величины действительного числа.

Абсолютная величина алгебраической суммы нескольких действительных чисел не больше суммы абсолютных величин слагаемых.

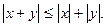
Абсолютная величина разности двух действительных чисел не меньше

разности абсолютных величин уменьшаемого и вычитаемого..

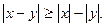
3. Абсолютная величина произведения действительных чисел равна произведению абсолютных величин сомножителей..

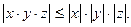
4. Абсолютная величина частного двух действительных чисел равна частному абсолютных величин делимого и делителя.

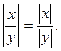
Переменной величиной называется такая величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной. Переменные величины обычно обозначаются буквами x, y, z, u, t,.., постоянные величины – a, b, c, ….

Множество всех числовых значений переменной величины называется областью изменения или областью значений этой величины.

Для указания вида областей изменения переменной величины х вводятся следующие понятия.

1. Замкнутый интервал или сегмент.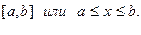

2. Открытый интервал или просто интервал: (а, b) или a < x < b.

3. Полузамкнутый или полуоткрытый интервалы: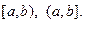

4. Бесконечные интервалы: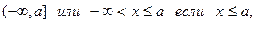

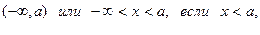
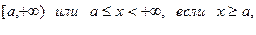
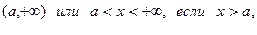
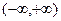- множество действительных чисел.

5. Окрестностью точки 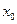называется любой открытый интервал, содержащий эту точку.

e-окрестностью точки 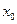называется открытый интервал, с центром в точке 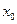, длиной 2e, т.е. интервал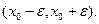

Логические символы, применяемые для краткой символической записи математических предложений:

" - “ любой ”, “ для всех ”, “ каков бы ни был ”. Пример: 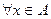- любой элемент множества A, 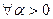- для любого положительного числа a.

$ - “существует ”, “ найдется ”. Пример: 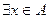- существует такой элемент множества А, что…, 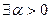- существует такое положительное число a, что…

Символы " и $ называются кванторами. " - квантор всеобщности, $ - квантор существования.

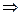- “ влечет за собой ”, “ следует ” – логическое следствие. Запись 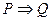означает, что из некоторого утверждения Р следует утверждение Q. (если имеет место Р, то имеет место и Q.) Например,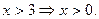

Û - “ эквивалентно ”, “ равносильно ”, логическая равносильность. Равносильность двух утверждений P и Q, 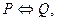означает, что 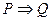и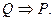

Литература: К.А. Хасеинов Каноны математики. Стр.124--128.

Лекция 10