Комплексные числа и действия над ними

Комплексным числом называется выражение вида 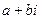, где а и b –действительные числа, а i – так называемая мнимая единица, определяемая равенством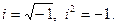

Числа а и b называются соответственно действительной и мнимой частями комплексного числа 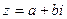и обозначаются a = Rez;. .

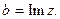Форма записи комплексных чисел в виде a + bi называется алгебраической формой комплексных чисел. Если а = 0, то число bi называется чисто мнимым, если b =0, то получаем действительное число. Таким образом, действительные числа являются частным случаем комплексных чисел. Комплексные числа 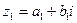и 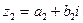считаются равными тогда и только тогда, когда 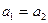и .

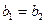Комплексные числа 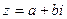и 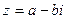, отличающиеся знаком мнимой части, называются сопряженными.

Каждому комплексному числу соответствует точка комплексной плоскости.

Комплексное число можно записать, используя полярную систему координат, в виде

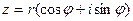
где r -полярный радиус точки М, 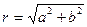. Число r называется модулем комплексного числа z, Полярный угол точки М, изображающей комплексное число z, равный φ, называется аргументом комплексного числа

z, φ = arg z

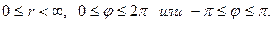
y

b M(a, b)

r

φ

O a x

Переход от записи комплексного числа в алгебраической форме 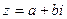к его записи в тригонометрической форме 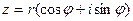и обратно совершается по формулам

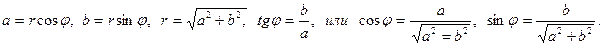
Аргумент комплексного числа определен с точностью до слагаемых, кратных 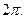В качестве главного значения аргумента выбирается значение, определяемое неравенством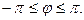

Аргумент z, 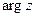, вычисляют по формулам: