
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи и примеры к разделу 9
|
|
Задача 9.5.1. Расчёт допускаемой ширины камер и ленточных междукамерных целиков (итерационный метод, детерминированный вариант)
Условие задачи
Определить допускаемую ширину камер и прочные размеры ленточных междукамерных целиков в следующих условиях:
налегающие породы:
| - мощность Н = 250 м; |
| - средний объёмный вес γ П = 26 кН/м3; |
| - средняя прочность на одноосное сжатие R П ср = 75 МПа; |
| - выход керна в кусках 100 мм и более - 50%; |
| - расстояние между главными нарушениями - 1, 0 м; |
| - характер нарушений - прерывные, поверхности не разделены, стенки прочные; |
| - приток воды в выработки, - 0 л/мин; |
| - направление простирания главных нарушений относительно длинной оси камеры - поперек; |
| - угол падения главных нарушений α = 80О от забоя; |
рудное тело:
| - мощность h = 10 м; |
| - угол падения β = 5О; |
| - средний объёмный вес руды γ Р = 35 кН/м3; |
| - временное сопротивление образцов кубической формы (ребро 5 см) одноосному сжатию: RР1 = 56 МПа; RР2 = 64 МПа; RР3 = 62 МПа; RР4 = 68 МПа; RР5 = 54 МПа. |
| - коэффициент структурного ослабления рудного массива КСО – 0, 9; |
| - длина камеры L – 100 м. |
Решение
Проявление горного давления при выполнении очистных работ в большей мере определяется горно-геологическими условиями разрабатываемого месторождения (или его участка) и принятой технологией горных работ.
Для обеспечения безопасности, высокой интенсивности и экономичности очистных работ необходимо выбрать оптимальный способ управления горным давлением.
В данной задаче рассматривается один из наиболее простых и распространенных способов управления горным давлением – оставление постоянных целиков. Это единственный способ, обеспечивающий сохранение равновесия налегающий и вмещающих пород. Зона влияния выработок невелика, опорное давление проявляется резко. Количество выделяемой энергии до достижения нового условия равновесия незначительно. Горное давление проявляется в виде деформации обнажений пород в камерах и дополнительных (к ранее существующим в массиве) нагрузках на оставляемые целики.
С экономической точки зрения применение этого способа целесообразно при разработке малоценных полезных ископаемых (каменной соли, мрамора, гипса, песчаника и др.) или при разработке месторождений бедной руды.
Оставление постоянных целиков также может быть обусловлено сложными гидрогеологическими условиями, необходимостью сохранить поверхность от оседания и обрушения в связи с наличием рек, озер, ответственных сооружений и т.д.
Полезное ископаемое и вмещающие породы должны быть достаточно устойчивыми.
По своему виду целики могут быть ленточными и изолированными (в данной задаче рассматриваются ленточные).
Выбранные размеры целиков должны обеспечивать безопасность и экономическую эффективность (излишние размеры целиков увеличивают потери полезного ископаемого).
Прочные размеры целиков выбирают на основе:
- расчетов;
- исследований на моделях;
- опытным путем на основе данных практики разработки аналогичных месторождений.
В настоящее время для сокращения потерь полезного ископаемого в целиках получили широкое применение искусственные целики из твердеющей смеси (заполнение отработанных камер твердеющим раствором с последующим извлечением целиков полезного ископаемого). Данная технология позволяет разрабатывать месторождения богатых руд.
1. Расчетная схема (рис.1).
|

Рис. 1. Расчетная схема к определению допускаемой ширины камер и ленточных междукамерных целиков
2. Определение допускаемой ширины камер.
Принимая во внимание небольшую глубину расположения выработок (250 м), допускаемую ширину камер определим по методике ЮАР.
По методике ЮАР показатель устойчивости обнажения:
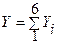 , баллы
, баллы
| где | Yi | - | баллы по учитываемым факторам, определяемые по методике ЮАР (приложения 3 – 9), баллы. |
а) Для определения количества баллов по первому фактору рассчитаем среднее значение прочности породы на одноосное сжатие RРср:
 , МПа
, МПа
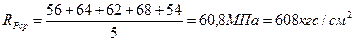
По приложению 3 находим Y1
Y1 = 7 баллов (т.к. сопротивление породы одноосному сжатию RРср находится в пределах > 500 < 1000 кгс/см2).
б) По приложению 4 находим Y2
Y2 = 8 баллов (т.к. выход керна = 25 %).
в) По приложению 5 находим Y3
Y3 = 20 баллов (т.к. величина расстояния между главными нарушениями в массиве = 1000 мм).
г) По приложению 6 находим Y4
Y4 = 25 баллов (т.к. нарушения прерывные, поверхности не разделены, стенки нарушений прочные).
д) По приложению 7 находим Y5
Y5 = 10 баллов (т.к. приток воды на 10 м выработки = 0 л/мин).
е) По приложениям 8, 9 находим Y6
Y6 = 0 баллов (т.к. простирание нарушений перпендикулярно оси выработки, угол падения нарушений от забоя и находится в пределах > 45о < 90о).
Сумма баллов Y = 7 + 8 + 20 + 25 + 10 – 0 = 70 баллов
По сумме баллов определяем класс породы (приложение 10). При Y = 70 баллов, класс породы II (характеристика хорошая).
Учитывая класс породы (II), определяем эквивалентный пролет АЭ по графику зависимости пролета выработки от времени ее устойчивого состояния (приложение 11, рис. 37).
По графику получили, что АЭ = 15 м при сроке службы 1 месяц.
Т.к. камера не является протяженной выработкой, необходимо определитьее допускаемую ширину А с учетом ее длины L:
Из формулы
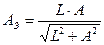 , м
, м
выразим 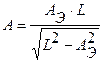 , м
, м
| где | А | - | допускаемая ширина камеры, м; |
| АЭ | - | эквивалентный пролет, м; | |
| L | - | длина камеры, м. |
Допускаемая ширина А камеры составит:
 м
м
Принимаем допускаемую ширину камеры А = 15 м.
3. Определение ширины междукамерных ленточных целиков.
При расчете прочных размеров междукамерных целиков необходимо решить две задачи:
- определить величину нагрузки на целик;
- определить несущую способность целика.
Ввиду большой сложности, эти задачи имеют только приближенные инженерные решения.
Так за нагрузку на целик принимается полный вес приходящихся на него налегающих пород до земной поверхности (рис. 1).
Тогда ширина ленточных междукамерных целиков определяется по формуле:
 , м
, м
| где | А | - | ширина камеры, м; |
| Н | - | мощность толщи налегающих пород, м; | |
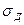
| - | удельная (на 1 м2) несущая способность целика, кПа; | |
| h | - | высота целика (мощность рудного тела), м; | |
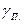
| - | объемный вес налегающих пород, кН/м3; | |
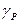
| - | объемный вес материала целика (в данной задаче - руды), кН/м3. |
За удельную несущую способность целика  акад. Шевяков Л.Д. принимает допускаемое напряжение при испытании образцов из материала целика на одноосное сжатие. При этом коэффициент структурного ослабления массива целика и форма его поперечного сечения (a/h) не учитывается, что вносит большую погрешность в результат расчета ширины целика.
акад. Шевяков Л.Д. принимает допускаемое напряжение при испытании образцов из материала целика на одноосное сжатие. При этом коэффициент структурного ослабления массива целика и форма его поперечного сечения (a/h) не учитывается, что вносит большую погрешность в результат расчета ширины целика.
Наиболее точно удельная несущая способность целика определяется итерационным методом проф. Панина И.М. (детерминированный и статистический варианты). За основу принимается временное сопротивление сжатию образцов из материала целика кубической формы, а также учитываются коэффициент структурного ослабления массива целика и его форма поперечного сечения (a/h).
В данной задаче расчет ширины междукамерных целиков ведется итерационным методом (детерминированный вариант).
Удельная несущая способность целика  определяется по формуле:
определяется по формуле:
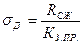 , кПа
, кПа
| где | Rсж | - | временное сопротивление руды на одноосное сжатие по данным испытания образцов кубической формы, кПа; |
| КЗ.ПР. | - | коэффициент запаса прочности (по Шевякову Л.Д. КЗ.ПР = 2 – 3). |
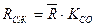 , кПа
, кПа
| где | 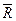
| - | среднее значение временного сопротивления сжатию образцов руды кубической формы, кПа; |
| КСО | - | коэффициент структурного ослабления массива. |
Определим среднее значение временного сопротивления сжатию образцов руды кубической формы 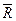 .
.
 , кПа
, кПа
| где | Rрi | - | временное сопротивлениена одноосное сжатие i -го образца руды кубической формы, кПа; |
| n | - | общее число испытаний образцов. |
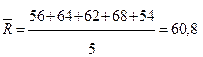 МПа = 60, 8 · 103 кПа
МПа = 60, 8 · 103 кПа
Расчитаем временное сопротивление на сжатие руды в массиве:  = 60, 8 · 103 · 0, 9 = 54, 72 МПа = 54720 кПа
= 60, 8 · 103 · 0, 9 = 54, 72 МПа = 54720 кПа
Допускаемое напряжение  в целиках по данным испытания образцов кубической формы (далее кубиковая прочность) составит:
в целиках по данным испытания образцов кубической формы (далее кубиковая прочность) составит:
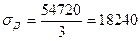 кПа
кПа
а а0 по кубиковой прочности  :
:
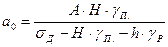 , м
, м
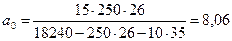 м
м
Далее, так как а0 ≠ h вносим первое уточнение в значение несущей способности целика:
 , кПа
, кПа
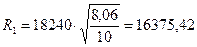 кПа
кПа
Находим новое значение ширины целика а1:
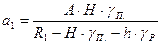 , м
, м
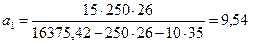 м
м
Рассчитав а0 и а1, мы определили нижний и верхний (т.е. наименьшее и наибольшее значения) пределы области значений ширины целика.
Далее расчет ведется по нижеприведенным формулам до тех пор, пока разница между соседними значениями а (т.е. |аi – а i-1|) не будет  0, 1 м. Графическое представление расчета ширины целиков итерационным методом представлен на рис. 2.
0, 1 м. Графическое представление расчета ширины целиков итерационным методом представлен на рис. 2.
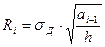 , кПа
, кПа
 , м
, м
 кПа;
кПа;
 м;
м;
| а2 – а1 | = |8, 36 – 9, 54| = 1, 18 м > 0, 1 м; продолжаем расчет
 кПа;
кПа;
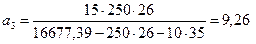 м;
м;
| а3 – а2 | = |9, 26 – 8, 36| = 0, 9 м > 0, 1 м; продолжаем расчет
 кПа;
кПа;
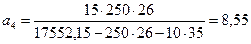 м;
м;
| а4 – а3 | = |8, 55 – 9, 26| = 0, 71 м > 0, 1 м; продолжаем расчет
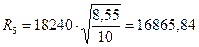 кПа;
кПа;
 м;
м;
| а5 – а4 | = |9, 1 – 8, 55| = 0, 55 м > 0, 1 м; продолжаем расчет
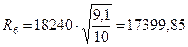 кПа;
кПа;
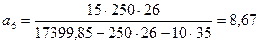 м;
м;
| а6 – а5 | = |8, 67 – 9, 1| = 0, 43 м > 0, 1 м; продолжаем расчет
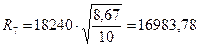 кПа;
кПа;
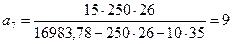 м;
м;
| а7 – а6 | = |9 – 8, 67| = 0, 33 м > 0, 1 м; продолжаем расчет
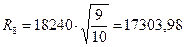 кПа;
кПа;
 м;
м;
| а8 – а7 | = |8, 74 – 9| = 0, 26 м > 0, 1 м; продолжаем расчет
 кПа;
кПа;
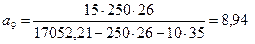 м;
м;
| а9 – а8 | = |8, 94 – 8, 74| = 0, 2 м > 0, 1 м; продолжаем расчет
 кПа;
кПа;
 м
м
| а10 – а9 | = |8, 79 – 8, 94| = 0, 15 м ≈ 0, 1 м; расчет окончен

Рис. 2. Расчет ширины целика итерационным методом
Принимаем ширину целика а = 8, 9 м при R ≈ 17, 1 МПа
Задание для самостоятельного решения
Определить допускаемую ширину камер и прочные размеры ленточных междукамерных целиков в условиях, приведенных в табл. 1.
Таблица 1.
| Показатель | Значения по вариантам | |||||
| 1 | 2 | 3 | ||||
| налегающие породы: | ||||||
| мощность Н, м | ||||||
| средний объёмный вес, γ П, кН/м3 | ||||||
| налегающие породы: | ||||||
| средняя прочность на одноосное сжатие R П ср , МПа | ||||||
| выход керна 100 мм и более, % | ||||||
| расстояние между главными нарушениями, м | 1, 5 | 1, 0 | 1, 0 | |||
| характер нарушений | прерывные, поверхности не разделены, стенки прочные | |||||
| приток воды в выработки, л/мин | ||||||
| Направление простирания главных нарушений относительно длинной оси камеры | вдоль | поперёк | вдоль | |||
| угол падения главных нарушений α, град | ||||||
| рудное тело: | ||||||
| мощность h, м | ||||||
| угол падения β, град | ||||||
| ср. объёмный вес руды γ Р , кН/м3 | ||||||
| временное сопротивление образцов кубической формы (ребро 5 см) одноосному сжатию, МПа | 50; 60; 65; 70; 75 | 55; 65; 75; 70; 60 | 50; 60; 70; 80; 55 | |||
| коэффициент структурного ослабления рудного массива КСО | 0, 85 | 0, 8 | 0, 9 | |||
| длина камеры L, м | ||||||
 Н
h
Н
h  a A
a A