
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построить линии влияния .
|
|
Расчетная схема балки изображена на рис. 5.
В расчетной схеме приняты следующие обозначения: длина пролета – L, длина консоли – b, расстояние от опоры А до точки С – a, расстояние от опоры А до точки приложения единичной подвижной нагрузки - X. Размеры балки приведены в табл. 5.1, а в приложении приведены данные соответствующего варианта.
Величину a выбирают из условий:
при X < 0 а = 1 м;
при 0 < X < l/2 a = 2 м;
при l/2< X< l a=3 м;
при l < X a = 4 м.
Таблица 5.1
| Показатель | Группа | |||||
| l, м | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
| b, м | 3.0 | 3.5 | 3.0 | 3.5 | 3.0 | 3.5 |
1. Определить и построить Л.В. реакций опор.
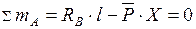 ;
;  . При
. При 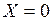 ;
; 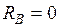 . При
. При 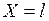 ;
;  . Строим
. Строим  , (см. рис. 5).
, (см. рис. 5).
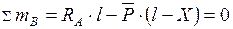 ;
; 
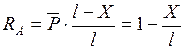 . При
. При 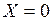 ;
; 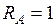 . При
. При 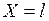 ;
; 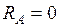 . Строим
. Строим 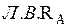 , (рис. 5).
, (рис. 5).
Определить и построить Л.В. 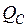 – поперечной силы в сечении
– поперечной силы в сечении 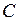 .
.
а) Положение груза 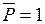 справа от
справа от 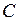 . Рассмотрим левую отсеченную
. Рассмотрим левую отсеченную
часть при 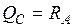 . Строим действительную часть
. Строим действительную часть 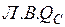 справа
справа 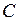 .
.
б) Положение груза 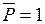 слева от
слева от 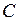 . Рассмотрим правую отсеченную часть при
. Рассмотрим правую отсеченную часть при 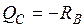 . Строим действительную часть
. Строим действительную часть 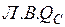 слева от
слева от 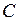 .
.
Определяем значение единичных ординат в сечении С.
Определить и построить Л.В. 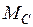 – изгибающего момента в сечении
– изгибающего момента в сечении 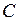 .
.
в) Положение груза 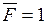 справа от
справа от 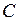 . Рассмотрим левую отсеченную часть.
. Рассмотрим левую отсеченную часть. 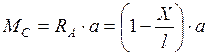 . При
. При 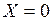 ;
; 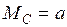 .
.
При 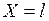 ;
; 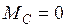 . Строим действительную часть
. Строим действительную часть 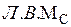 по ординатам справа от
по ординатам справа от 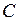 .
.
г) Положение груза 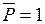 слева от
слева от 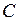 . Рассмотрим правую отсеченную часть при
. Рассмотрим правую отсеченную часть при 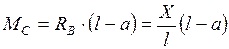 . При
. При 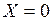 ;
; 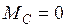 . При
. При 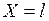 ;
; 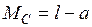 .
.
Строим действительную часть 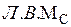 по ординатам слева от
по ординатам слева от 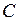 . Ордината пересечения правой и левой ветви определяет значение момента в сечении
. Ордината пересечения правой и левой ветви определяет значение момента в сечении 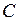 .
.
При 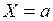 значение момента слева–справа
значение момента слева–справа
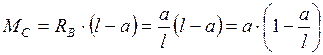 .
.
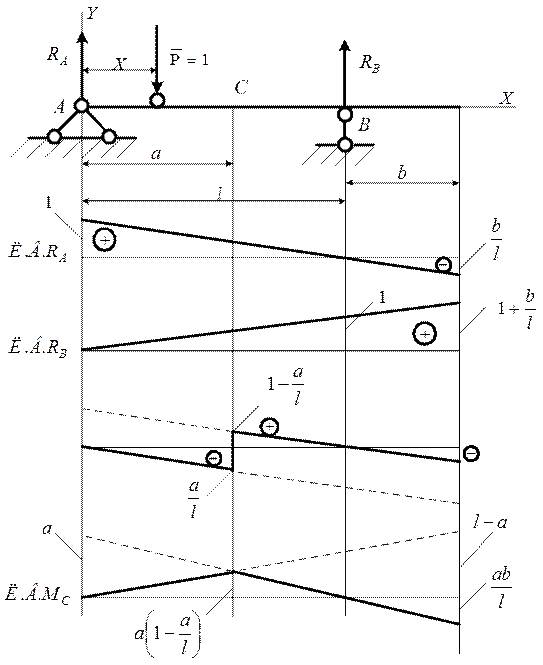
Рис. 5. Двухшарнирная балка с правой консолью
Задача № 6
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР НАСТЕННОГО КРАНА С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ
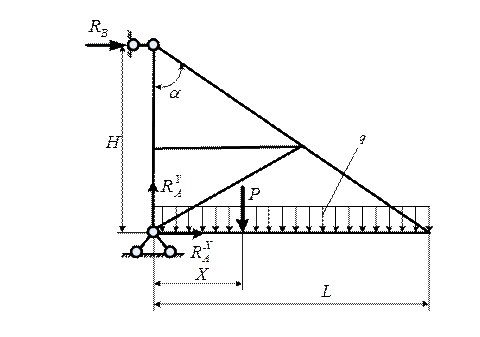
Рис. 6.1. Схема настенного крана
Кран загружен весом консоли и подвижной крановой нагрузкой
Требуется построить линии влияния реакций опор 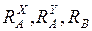 для настенного крана и определить указанные величины от действия сосредоточенной силы Р и распределенной нагрузки q при заданном значении X.
для настенного крана и определить указанные величины от действия сосредоточенной силы Р и распределенной нагрузки q при заданном значении X.
Расчетная схема настенного крана приведена на рис.6.1. В расчетной схеме приняты следующие обозначения: геометрические параметры настенного крана H и L, сосредоточенная нагрузка Р, распределенная нагрузка q.
Размеры настенного крана и нагрузки приведены в табл.6.1, а в приложении приведены данные соответствующеговарианта.
Таблица 6.1
| Показатель | Группа | |||||
| H, м | ||||||
| L, м | ||||||
| P, кН | ||||||
| q, кН/м | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 |
Численный пример:
Исходные данные: 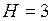 м;
м; 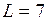 м;
м; 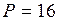 кН;
кН; 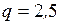 кН/м;
кН/м;
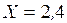 м.
м.
Приведем упрощенную расчетную схему при действующей единичной подвижной нагрузке, рис. 6.2 а.
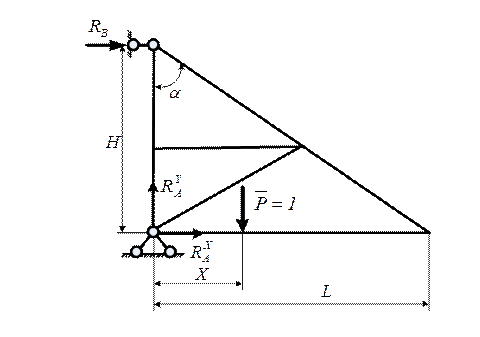
Рис. 6.2. Упрощенная расчетная схема
Для построения линии влияния 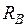 запишем уравнение моментов относительно
запишем уравнение моментов относительно 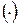 А:
А:
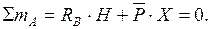 (6.1)
(6.1)
Отсюда 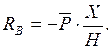 (6.2)
(6.2)
Строим линии влияния 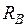 (рис. 6.3), задав некоторые значения
(рис. 6.3), задав некоторые значения 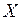 в уравнении (6.2):
в уравнении (6.2):
При 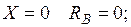 при
при 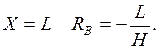
Для построения линии влияния 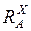 запишем уравнение моментов относительно
запишем уравнение моментов относительно 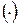 В:
В:
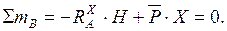 (6.3)
(6.3)
Отсюда 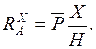 (6.4)
(6.4)
Строим линии влияния 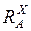 (рис. 6.3), задав некоторые значения
(рис. 6.3), задав некоторые значения 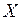 в уравнении (6.4):
в уравнении (6.4):
При 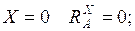 при
при 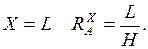
Зависимость 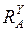 определяем из суммы проекций на ось Y:
определяем из суммы проекций на ось Y:
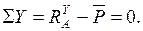 (6.5)
(6.5)
Отсюда 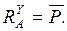
Строим линии влияния 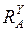 (рис. 6.3).
(рис. 6.3).
Применяя принцип пропорциональности и независимости действия сил, определяем реакции в опорах от действия сосредоточенной силы Р и распределенной нагрузки q.
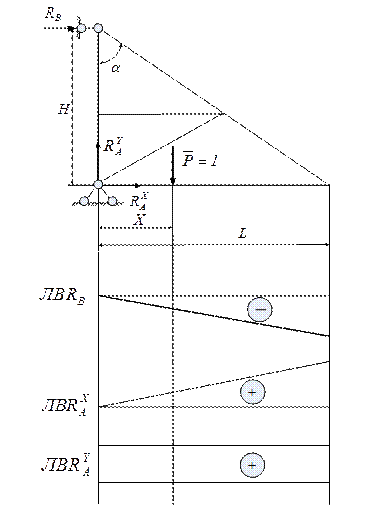
Рис. 6..3. Линии влияния
Задача № 7
ОПРЕДЕЛЕНИЕ ПОПЕРЕЧНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА НА КОНСОЛИ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ
Построить линии влияния 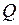 и
и 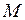 на консоли в заданном сечении.
на консоли в заданном сечении.
Определить силу 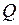 и момент
и момент 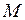 от действия сосредоточенной силы
от действия сосредоточенной силы 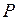 и распределенной нагрузки
и распределенной нагрузки 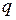 .
.
На рис.7 приведена расчетная схема балки. В расчетной схеме приняты следующие обозначения: сосредоточенная сила – Р, распределенная нагрузка - q, расстояния между опорами - L, расстояние от шарнирной подвижной опоры В до точки F – C, расстояние от точки F до конца консоли балки – К.
Размеры балки и величины действующих нагрузок приведены в табл.7.1, а в приложении приведены данные соответствующего варианта.
Таблица 7.1
| Показатель | Группа | |||||
| Р, кН | ||||||
| q,, кН/м | ||||||
| L, м | ||||||
| C, м | ||||||
| К, м |
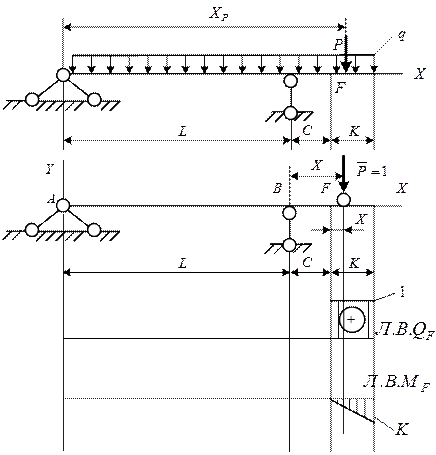
Рис. 7. Л.В. поперечных сил и моментов на консоли балки
Численный пример:
Исходные данные: 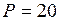 кН;
кН; 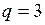 кН/м;
кН/м; 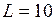 м;
м; 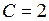 м;
м; 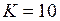 м;
м; 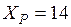 м.
м.
На первом этапе рассмотрим действие на балку с консолью единичной подвижной нагрузки 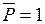 . Определяем реакции опор
. Определяем реакции опор 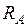 и
и 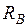 .
.
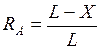 ;
;
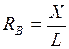 .
.
Для построения линий влияния поперечных сил на консоли рассмотрим два случая положений единичной силой 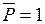 .
.
1. Сила 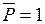 слева от сечения
слева от сечения  .
. 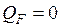 .
. 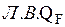 слева от
слева от  равна нулю.
равна нулю.
2. Сила 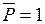 справа от сечения
справа от сечения  .
. 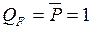 .
. 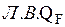 справа от
справа от  равна единице.
равна единице.
Для построения линий влияния моментов изгибающих на консоли рассмотрим два случая положения единичной силой 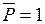 .
.
1. Сила 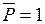 слева от сечения
слева от сечения  , рассматриваем правую часть.
, рассматриваем правую часть. 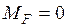 .
. 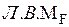 слева от
слева от  равна нулю.
равна нулю.
2. Сила 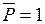 справа от сечения
справа от сечения  , рассматриваем левую часть.
, рассматриваем левую часть.
 (7.1)
(7.1)
Подставляя значения 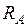 и
и 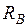 получим:
получим:
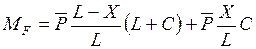 (7.2)
(7.2)
В уравнении (7.2) подставляем значения 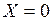 и
и 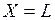 . По этим данным строим линию влияния изгибающего момента в
. По этим данным строим линию влияния изгибающего момента в 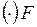 , (см.рис. 7).
, (см.рис. 7).
Применяя принцип независимости действия сил и пропорциональности, определяем перерезывающую силу 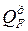 и изгибающий момент
и изгибающий момент 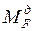 от действия сосредоточенной силы Р и распределенной нагрузки q.
от действия сосредоточенной силы Р и распределенной нагрузки q.
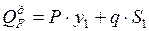 (7.3)
(7.3)
 (7.4)
(7.4)
Где 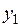 и
и 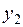 – соответствующие ординаты линий влияния
– соответствующие ординаты линий влияния 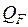 и
и 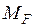 ;
;
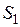 и
и 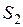 – соответствующие площади линий влияния
– соответствующие площади линий влияния 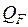 и
и 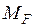 .
.
Задача № 8
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ С ПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ ОТ ЕДИНИЧНОЙ ПОДВИЖНОЙ НАГРУЗКИ
Построить линии влияния усилий в стержнях 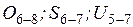 .
.
Вычислить величины указанных усилий в сечении 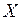 . Езда по нижнему поясу.
. Езда по нижнему поясу.
На рис.8.1 приведена расчетная схема фермы. В расчетной схеме приняты следующие обозначения: высота фермы – H, длина панели – a, угол наклона раскоса – 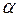 . Геометрические размеры фермы приведены в табл.8.1, а в приложении приведены данные соответствующего варианта.
. Геометрические размеры фермы приведены в табл.8.1, а в приложении приведены данные соответствующего варианта.
Таблица 8.1
| Показатель | Группа | |||||
| H, м | 1, 0 | 1, 3 | 1, 5 | 1, 7 | 1, 9 | 2, 1 |
| a, м | 1, 5 | 1, 5 | 1, 5 | 1, 5 | 1, 5 | 1, 5 |
Численный пример:
Исходные данные:
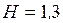 м;
м; 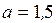 м;
м; 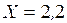 м. Проводим сечение
м. Проводим сечение 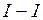 при пересечении не более 3-х стержней.
при пересечении не более 3-х стержней.
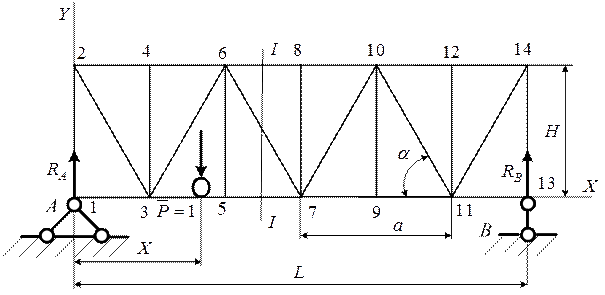
Рис. 8.1. Схема фермы с подвижной нагрузкой по нижнему поясу
Определим угол наклона раскоса 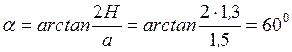 .
.
Строим линии влияния опорных реакций, см. задачу № 5.
Для построения 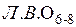 выберем моментную точку
выберем моментную точку 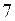 , см. рис. 8.2 (два других стержня пересекаются в точке 7).
, см. рис. 8.2 (два других стержня пересекаются в точке 7).
Составим уравнение моментов:
а) груз находится справа от сечения, запишем уравнение моментов левой отсеченной части 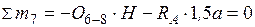 ;
;
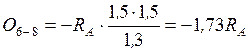 . Откладываем
. Откладываем 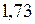
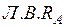 со знаком минус. Действительная ветвь расположена от узла
со знаком минус. Действительная ветвь расположена от узла 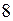 , ближайшего от сечения, т.к. передача нагрузки происходит в узлах фермы, до опоры
, ближайшего от сечения, т.к. передача нагрузки происходит в узлах фермы, до опоры 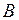 , т.е. в загруженной части фермы.
, т.е. в загруженной части фермы.
б) груз находится слева от сечения, запишем уравнение моментов правой отсеченной части 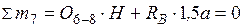 ;
;
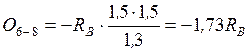 . Откладываем
. Откладываем 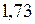
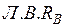 со знаком минус.
со знаком минус.
Действительная ветвь расположена от узла 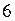 до опоры
до опоры 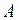 . Соединим точку 6 на левой прямой и точку 8 на правой прямой
. Соединим точку 6 на левой прямой и точку 8 на правой прямой 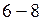 , называемой передаточной прямой.
, называемой передаточной прямой.
Для построения 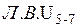 берем моментную точку
берем моментную точку 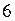 . Составим уравнение моментов:
. Составим уравнение моментов:
а) груз находится справа от сечения, запишем уравнение моментов левой отсеченной части 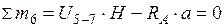 ;
; 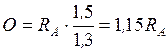 . Откладываем
. Откладываем 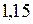
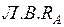 со знаком плюс. Действительная ветвь расположена от узла
со знаком плюс. Действительная ветвь расположена от узла 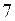 до опоры
до опоры 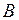 , т.е. в загруженной части фермы.
, т.е. в загруженной части фермы.
б) груз находится слева от сечения, запишем уравнение моментов правойотсеченной части 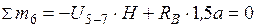 ;
; 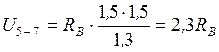 .
.
Откладываем 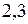
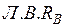 со знаком плюс. Действительная ветвь расположена от узла
со знаком плюс. Действительная ветвь расположена от узла 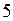 до опоры
до опоры 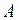 . Строим передаточную прямую между узлами
. Строим передаточную прямую между узлами 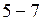 .
.
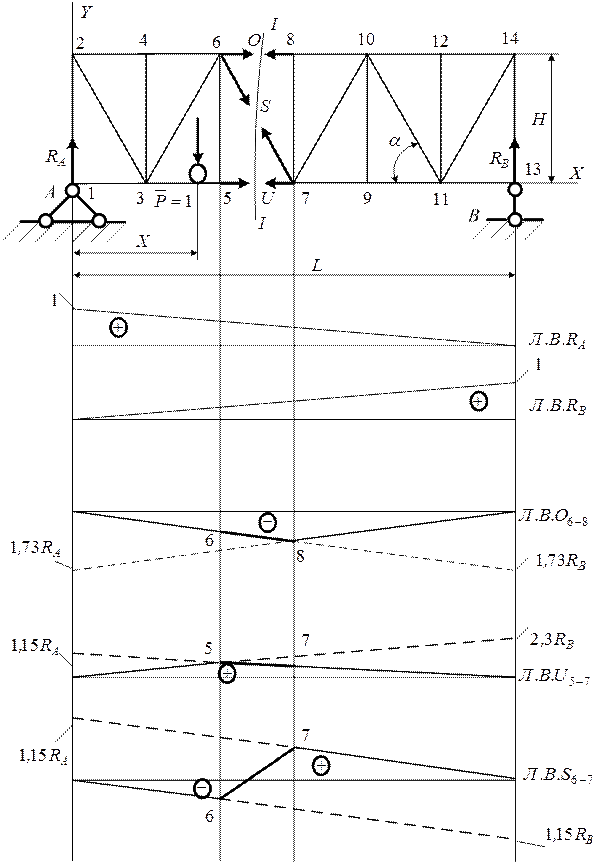
Рис. 8.2. Линии влияния в сечении 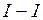
Примечание: При построении линий влияния 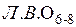 и
и 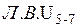 следует помнить – пересечение линий влияния левых и правых ветвей должно происходить в моментных точках, т.е.в
следует помнить – пересечение линий влияния левых и правых ветвей должно происходить в моментных точках, т.е.в 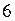 и
и 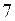 .
.
Для построения линий влияния в раскосе 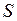 используем способ проекций, рассмотривая левую и правую отсеченные части отдельно.
используем способ проекций, рассмотривая левую и правую отсеченные части отдельно.
а) груз находится справа от сечения, рассмотрим равновесие левой отсеченной части как сумму проекций сил на ось 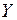 :
: 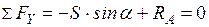 ;
; 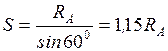 . Откладываем
. Откладываем 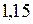
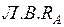 со знаком плюс от узла
со знаком плюс от узла 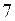 до опоры
до опоры 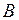 .
.
б) груз находится слева от сечения, рассмотрим равновесие правой отсеченной части как сумму проекций сил на ось 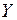 :
: 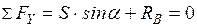 ;
; 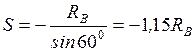 . Откладываем
. Откладываем 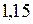
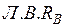 со знаком минус от узла
со знаком минус от узла 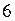 до опоры
до опоры 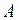 . Строим передаточную прямую между узлами
. Строим передаточную прямую между узлами 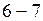 .
.
Для построения линий влияния в стойках используем способ вырезания узлов как частный случай способа проекций, см. рис. 8.3. Вырежем узел 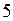 .
.
а) при езде понизу нагрузка находится вне узла 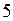 . Сумма проекций сил на ось
. Сумма проекций сил на ось 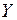 :
: 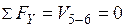 .
.
б) при езде понизу нагрузка находится в узле 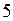 . Сумма проекций сил на ось
. Сумма проекций сил на ось 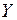 :
: 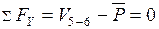 ;
; 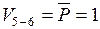 .
.
Отложим положительную ординату в сечении узла 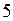 . Соединим смежные узлы переходными прямыми, получим
. Соединим смежные узлы переходными прямыми, получим 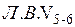 . При езде поверху
. При езде поверху 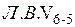 будет нулевой линией.
будет нулевой линией.
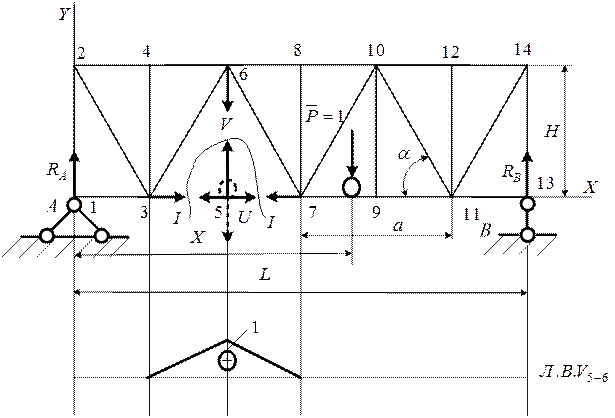
Рис. 8.3. Линии влияния в стойках
Задача № 9
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР И ИЗГИБАЮЩЕГО МОМЕНТА В ПРОЛЕТЕ БАЛКИ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ ОТ ДЕЙСТВИЯ СИСТЕМЫ СОСРЕДОТОЧЕННЫХ СИЛ И РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
На рис. 9.1 представлена расчетная схема.
В расчетной схеме приняты следующие обозначения: пролет балки – L, длина консоли балки – b, сосредоточенные нагрузки от колес тележки – 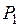 и
и 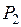 , распределенная нагрузка – q, расстояние от опоры до сечения C в пролете балки – a, расстояние между колесами тележки – d.
, распределенная нагрузка – q, расстояние от опоры до сечения C в пролете балки – a, расстояние между колесами тележки – d.
Геометрические размеры балки и действующие на нее •нагрузки приведены в табл.9.1, а в приложении приведены данные соответствующего варианта.
Таблица 9.1
| Показатель | Группа | |||||
| L, м | 4, 0 | 5, 0 | 6, 0 | 4, 0 | 5, 0 | 6, 0 |
| b, м | 4, 0 | 3, 5 | 3, 0 | 4, 0 | 3, 5 | 3, 0 |
| a, м | 1, 0 | 2, 0 | 3, 0 | 1, 5 | 2, 5 | 3, 5 |
| d, м | 0, 4 | 0, 6 | 0, 8 | 1, 0 | 1, 2 | 1, 4 |
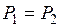 , кН , кН
| ||||||
| q, кН/м | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 |
Численный пример:
Исходные данные: 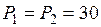 кН;
кН; 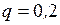 кН/м;
кН/м; 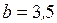 м;
м; 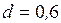 м;
м; 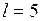 м;
м; 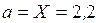 м.
м.
В виду симметрии нагрузки от двухосной тележки, упростим расчетную схему.
На рис. 9.2 дана упрощенная схема. Строим 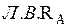 и
и 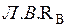 . Затем строим
. Затем строим 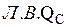 и
и 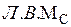 , см. задачу № 8.
, см. задачу № 8.
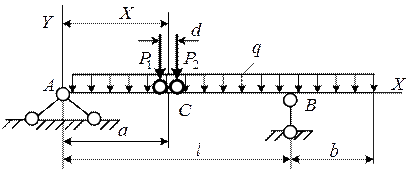
Рис. 9.1. Схема балки с распределенной нагрузкой и грузовой тележкой
Определим значения сил и моментов в указанном сечении 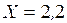 м.
м.
Т.к. значения сосредоточенных сил на оси равны, установим тележку одной осью на вершину линий влияния, 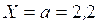 м.
м.
Для определения максимальных значений, вторую ось необходимо расположить на более пологой ветви, т.е. иметь большие значения сил и моментов. В нашем примере, вторые оси расположим справа от максимумов 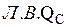 и
и 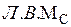 .
.
Вычисление значений реакций 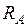 и
и 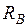 .
.
а) Определим ординаты на 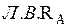 под сосредоточенными силами
под сосредоточенными силами 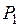 и
и 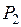 . Составим пропорции с учетом
. Составим пропорции с учетом 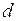 . При этом тележку размещаем слева от
. При этом тележку размещаем слева от 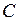 , см. рис. 9.3. Вычисляем ординаты под сосредоточенными силами.
, см. рис. 9.3. Вычисляем ординаты под сосредоточенными силами.
Реакция 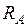 от сосредоточенных сил
от сосредоточенных сил
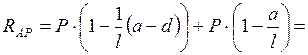
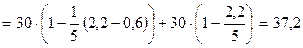 кН.
кН.
Реакция 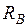 от сосредоточенных сил
от сосредоточенных сил
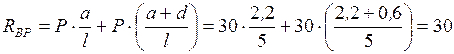 кН.
кН.
Реакции 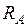 и
и 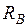 от распределенной нагрузки
от распределенной нагрузки 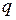 .
.
б) Определим площади 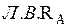 и
и 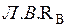 под распределенной нагрузкой с учетом знака, см. рис. 10.3.
под распределенной нагрузкой с учетом знака, см. рис. 10.3.
Реакция 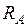 от распределенной нагрузки
от распределенной нагрузки
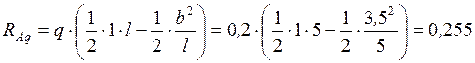 кН.
кН.
Реакция 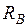 от распределенной нагрузки
от распределенной нагрузки
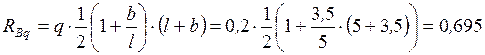 кН.
кН.
Полные реакции опор 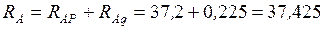 кН;
кН;
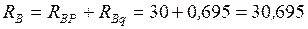 кН.
кН.
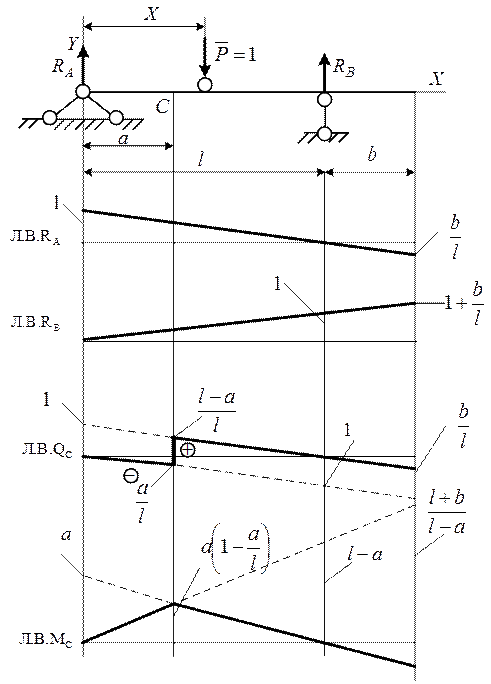
Рис. 9.2. Линии влияния реакций опор, поперечной силы и момента в сечении 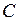
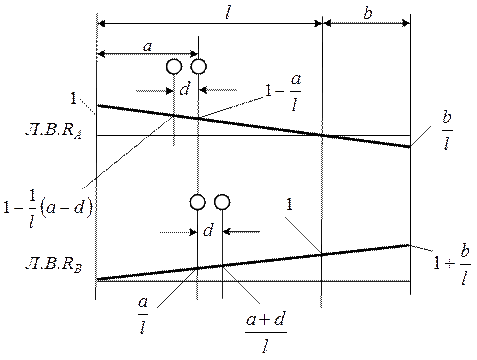
Рис. 9.3. Определение действительных реакций опор
Вычисление действительных значений поперечной силы 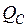 в сечении
в сечении 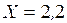
Представим 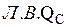 и
и 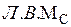 для вычисления действительных значений, см. рис. 9.4.
для вычисления действительных значений, см. рис. 9.4.
Предварительно определим ординаты линий влияния под грузовой тележкой.
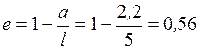 ;
; 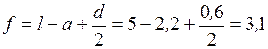 ;
;
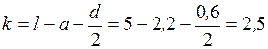 .
.
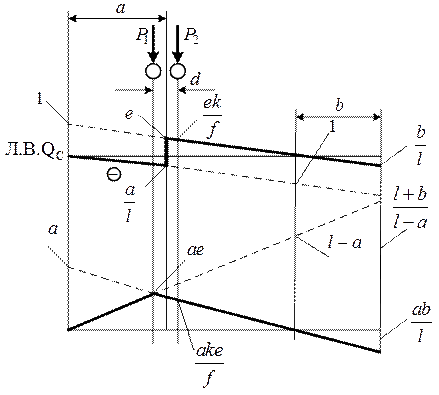
Рис. 9.4. Определение действительных значений поперечных сил и изгибающих моментов
Сила 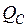 от сосредоточенных сил
от сосредоточенных сил
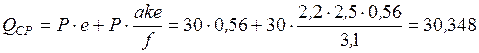 кН;
кН;
Сила 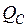 от распределенной нагрузки
от распределенной нагрузки
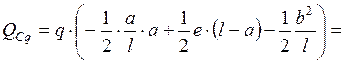
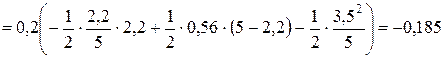 кН.
кН.
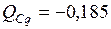 . Сумма
. Сумма 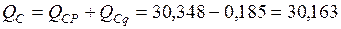 кН.
кН.
Момент изгибающий от сосредоточенных сил
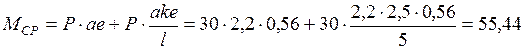 кНм;
кНм;
Момент изгибающий от распределенной нагрузки
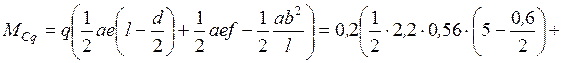
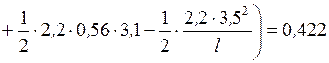 кНм.
кНм.
Сумма 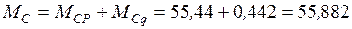 кНм.
кНм.
Задача № 10
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ С ПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ ОТ СОСРЕДОТОЧЕННОЙ И РАСПРЕДЕЛЕННОЙ НАГРУЗОК
Схема представлена на рис. 10.1.
В расчетной схеме приняты следующие обозначения: длина панели – a, высота фермы – H. длина пролета – L, расстояния между колесами тележки – d, распределенная нагрузка от собственного веса фермы – q, нагрузки на колеса от веса тележки с грузом – 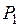 и
и 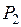 , расстояние от шарнирно-неподвижной опоры до оси тележки – X.
, расстояние от шарнирно-неподвижной опоры до оси тележки – X.
Размеры фермы и действующие нагрузки приведены в табл.10.1, а в приложении приведены данные соответствующего варианта.
Таблица 10.1
| Показатель | Группа | |||||
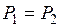 , кН , кН
| ||||||
| q, кН/м | ||||||
| d, м | 1, 0 | 1, 0 | 1, 0 | 1, 0 | 1, 0 | 1, 0 |
| H, м | 2, 5 | 2, 3 | 2, 1 | 1, 9 | 1, 7 | 1, 5 |
| a, м | 1, 5 | 1, 5 | 1, 5 | 1, 5 | 1, 5 | 1, 5 |
Численный пример:
Исходные данные: 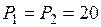 кН;
кН; 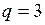 кН/м;
кН/м; 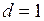 м;
м; 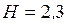 м;
м; 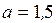 м;
м; 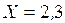 м.
м.
Вычислить действительные значения сил и моментов от сосредоточенных сил и распределенной нагрузки в элементах фермы 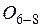 ;
; 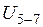 ;
; 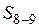 .
.
Определим угол наклона раскоса 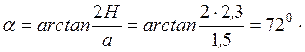
Сечением 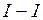 рассекаем три стержня: элементы верхнего пояса
рассекаем три стержня: элементы верхнего пояса 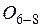 и нижнего пояса
и нижнего пояса 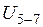 и раскоса
и раскоса 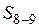 , требующих определения усилий.
, требующих определения усилий.
На рис. 10.2 изображена упрощенная схема фермы с разрезами панелей.
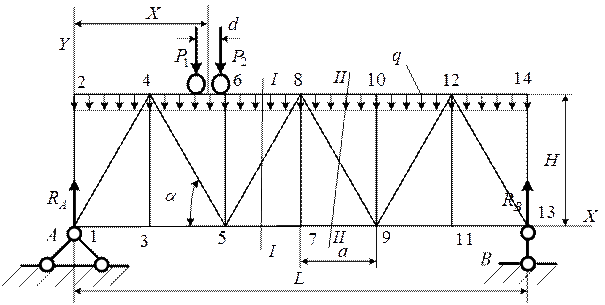
Рис.10.1. Расчетная схема фермы с ездой поверху
Для элемента 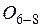 моментной точкой является
моментной точкой является 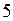 .
.
а) Груз справа от 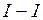 , рассматриваем левую отсеченную часть
, рассматриваем левую отсеченную часть
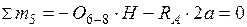 ;
;
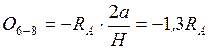 .
. 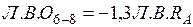 . Действительная правая
. Действительная правая
прямая – правая ветвь от узла 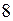 до
до 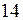 .
.
б) Груз слева от 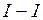 , рассматриваем правую отсеченную часть
, рассматриваем правую отсеченную часть
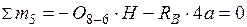 ;
;
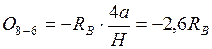 .
. 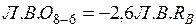 Действительная прямая – левая ветвь от узла
Действительная прямая – левая ветвь от узла 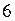 до
до 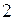 . Переходная прямая
. Переходная прямая 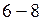 . Элемент верхнего пояса сжат.
. Элемент верхнего пояса сжат.
Рассмотрим 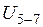 . Моментной точкой является
. Моментной точкой является 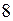 .
.
а) Груз справа от 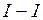 , рассматриваем левую отсеченную часть
, рассматриваем левую отсеченную часть
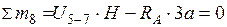 ;
; 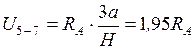 .
. 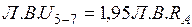 . Действительная прямая – правая ветвь от узла
. Действительная прямая – правая ветвь от узла 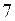 до
до  .
.
б) Груз слева от 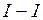 , рассматриваем правую отсеченную часть
, рассматриваем правую отсеченную часть
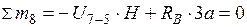 ;
;
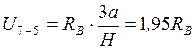 .
. 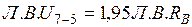 . Действительная прямая – левая ветвь от узла
. Действительная прямая – левая ветвь от узла 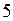 до
до 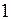 . Переходная прямая
. Переходная прямая 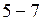 . Элемент нижнего пояса растянут.
. Элемент нижнего пояса растянут.
По сечению 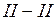 выделим раскос
выделим раскос 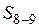 .
.
а) Груз справа от 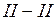 , рассматриваем левую отсеченную часть
, рассматриваем левую отсеченную часть
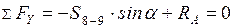 ;
;
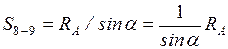 .
. 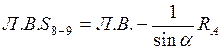 . Действительная положительная прямая – правая ветвь от узла
. Действительная положительная прямая – правая ветвь от узла 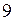 до
до  .
.
б) Груз слева от 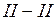 , рассматриваем правую отсеченную часть
, рассматриваем правую отсеченную часть
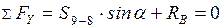 ;
;
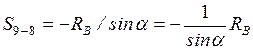 .
. 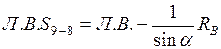 .
.
Действительная отрицательная прямая – левая ветвь от узла 8 до 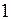 . Переходная прямая
. Переходная прямая 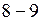 . Панель меняет сжатие на растяжение.
. Панель меняет сжатие на растяжение.
Вычисление действительных усилий в стержнях. Отдельно определим усилия от сосредоточенных сил и распределенной нагрузки.
Предварительно, необходимо вычислить ординаты под сосредоточенными силами, составив ряд пропорций, см. рис. 10.3.
Стержень 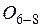 .
.
а) 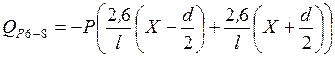 ;
;
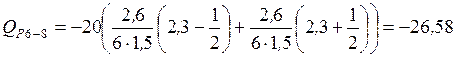 кН.
кН.
б) 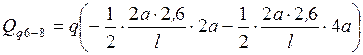 ;
;
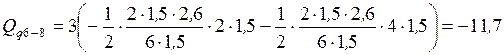 кН.
кН.
Суммарное усилие 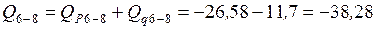 кН.
кН.
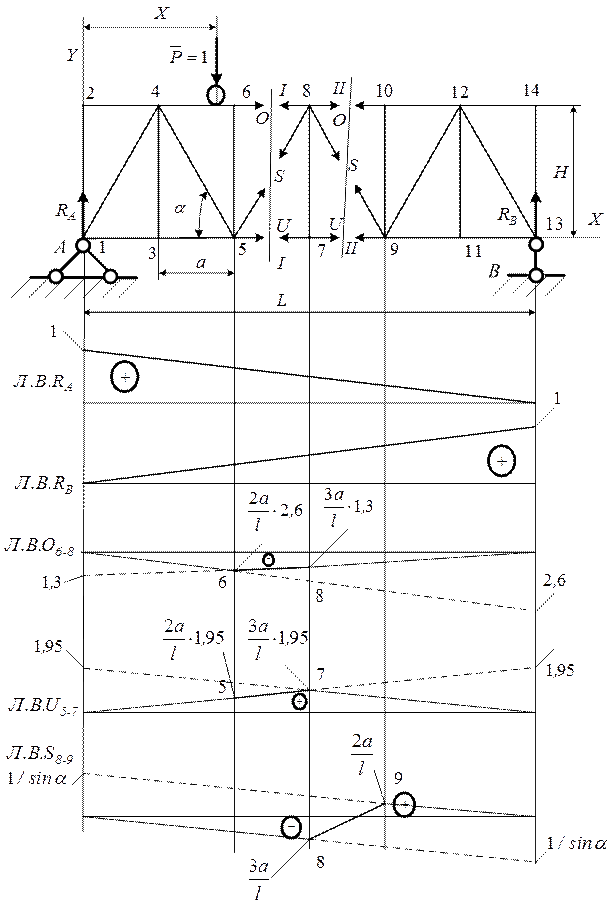
Рис. 10.2. Линии влияния 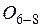 ;
; 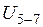 ;
; 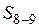
Стержень 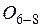 сжат.
сжат.
Стержень 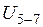 .
.
а) 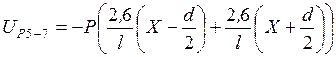 ;
;
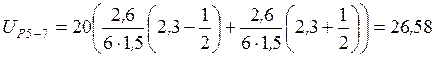 кН.
кН.
б) 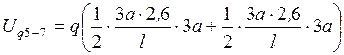 ;
;
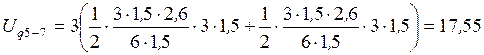 кН.
кН.
Суммарное усилие 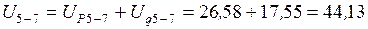 кН.
кН.
Стержень 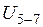 растянут.
растянут.
Стержень 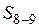 .
.
а) 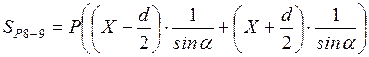 ;
;
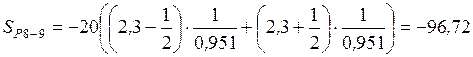 кН.
кН.
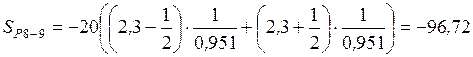 кН.
кН.
б) 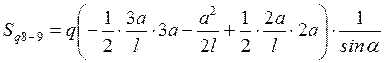 ;
;
Примечание: площадь на переходном участке 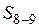 равна площади трапеции
равна площади трапеции
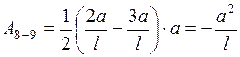 .
.
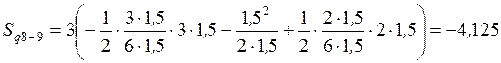 кН.
кН.
Суммарное усилие 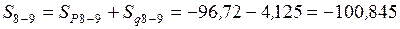 кН.
кН.
Стержень 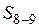 сжат.
сжат.
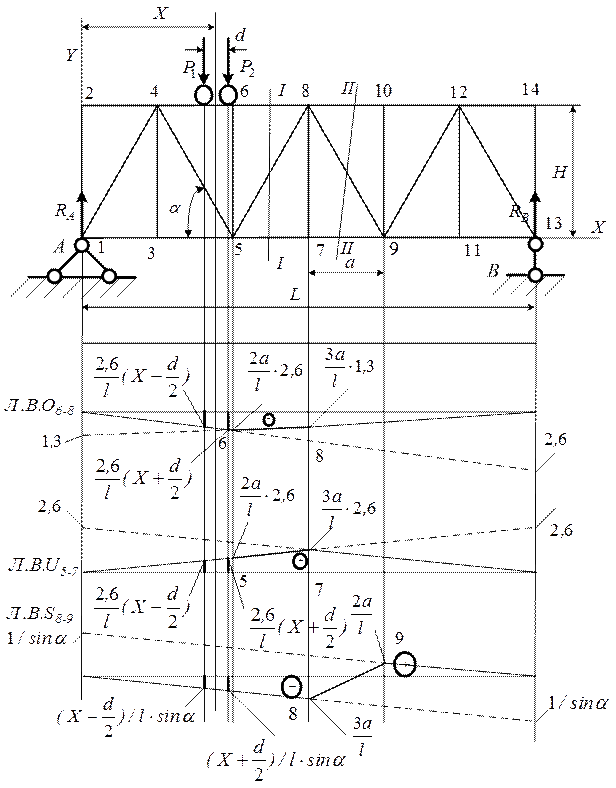
Рис. 10.3. Линии влияния с определением ординат
Список литературы к изучению дисциплины «Строительная механика и металлоконструкции»
1. Доркин В. В. Металлические конструкции: учебник / В. В. Доркин, М. П. Рябцева. - М.: Инфра-М, 2010. - 457 с.: ил.
2. Константинов И. А. Строительная механика: учебник / И. А. Константинов, В. В. Лалин, И. И. Лалина; Санкт-Петербургский государственный политехнический университет. - М.: Проспект, 2015. - 432 с.: ил. - Библиогр.: с. 420-421
3. Москалев Н. С. Металлические конструкции: учебник / Н. С. Москалев, Я. А. Пронозин. - М.: АСВ, 2010. - 344 с.: ил.
4. Юсупов А. К. Металлические конструкции в вопросах, в ответах и в проектировании / А. К. Юсупов. - М.: Типография ДНЦ РАН, 2010. - 807 с.: ил.