Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Картка-консультант
⇐ ПредыдущаяСтр 132 из 132
|
|
Картка-консультант
| № кроку | Алгоритм виконання | Розв’язання | |
| Завдання. Знайти проміжки зростання і спадання та екстремуми функції f(x)= 1/4х4 – 5/3x3 + 3x2 + 10 | |||
| Знаходимо похідну функції f'(x) | f'(x)= x3 – 5x2 + 6x | ||
| Знаходимо критичні точки при яких f'(x)=0 (Розкладаємо на множники) Критичні точки функції | x3 – 5x2 + 6x = 0 x(x2 – 5x + 6)=0 x(x – 2)(x – 3)=0 x1=0, x2=2, x3=3 | ||
| Знаходимо додатні та від’ємні проміжки f'(x) |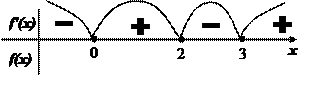  
| ||
| Визначаємо точки екстремумів. У критичних точках f'(x) змінює знак: якщо “ – ” на “ + ” тоді хmin якщо “ + ” на “ ‑ ” тоді хmax | Екстремуми функції: хmin: х1=0, х3=3 хmax: х2=2 | ||
| Визначаємо проміжки спадання та зростання функції f(x). Якщо f'(x)> 0, тоді f(x) зростає (ä) Якщо f'(x)< 0, тоді f(x) спадає (æ) |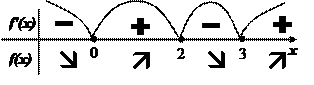 
Функції f(x) спадає напроміжку (-∞; 0) та (2; 3).
Функції f(x) зростає напроміжку (0; 2) та (3; ∞).
| ||
Картка-консультант
| № кроку | Алгоритм виконання | Розв’язання | |||||||||
| Завдання. | |||||||||||
| Знаходимо похідну функції f'(x) | |||||||||||
| Знаходимо критичні точки при яких f'(x)=0 (Розкладаємо на множники) Критичні точки функції | |||||||||||
| Знаходимо додатні та від’ємні проміжки f'(x) | 
| ||||||||||
| Визначаємо точки екстремумів. У критичних точках f'(x) змінює знак: якщо “ – ” на “ + ” тоді хmin якщо “ + ” на “ ‑ ” тоді хmax | Екстремуми функції: хmin: хmax: | ||||||||||
| Визначаємо проміжки спадання та зростання функції f(x). Якщо f'(x)> 0, тоді f(x) зростає (ä) Якщо f'(x)< 0, тоді f(x) спадає (æ) |
Функції f(x) спадає напроміжку Функції f(x) зростає напроміжку | ||||||||||