Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания лабораторной работы 1
|
|
1. Написать файл-функции для решения поставленных далее задач.
2. Сохранить их в отдельных m-файлах (среда Матлаб)
3. Выполнить и оформить в виде отчета поставленные далее задачи.
Задача №1. Решить задачу Коши на отрезке [x0, X] методом Рунге-Кутта четвертого порядка, применяя деление отрезка на N частей. Оценить погрешность.
Варианты заданий в табл.1.
Табл.1.
| № варианта | Уравнение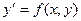 
| Начальное условие | [x0, X] | N |
| y'(x)=sin(xy2) | y(0)=1 | [0, 2] | 10 | |
| y'(x)=cos(x) + y2 | y(0)=2 | [0, 2] | 20 | |
| y'(x)= cos(xy2) | y(0)=3 | [0, 2] | 30 | |
y'(x)=sin 
| y(0)=1 | [0, 2] | 40 | |
y'(x)=tg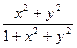 
| y(0)=2 | [0, 2] | 50 | |
| y'(x)=x + y2 | y(1)=3 | [1, 2] | 10 | |
y'(x)=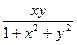 
| y(1)=1 | [1, 2] | 20 | |
y'(x)=cos 
| y(1)=2 | [1, 2] | 30 | |
y'(x)=sin (x  )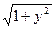
| y(1)=3 | [1, 2] | 40 | |
y'(x)=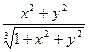 
| y(1)=1 | [1, 2] | 50 | |
| y'(x)=x ln(1+y2) | y(1)=2 | [1, 3] | 10 | |
| y'(x)=y cos(x+y2) | y(1)=3 | [1, 3] | 20 | |
| y'(x)=ex x+y2 | y(1)=1 | [1, 3] | 30 | |
| y'(x)=sin(x(1+y2)) | y(1)=2 | [1, 3] | 40 | |
y'(x)=lg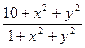 
| y(1)=3 | [1, 3] | 50 | |
| y'(x)=x+y2 3x | y(-1)=1 | [-1, 1] | 10 | |
| y'(x)=|x-y|(1+x2+y2) | y(-1)=2 | [-1, 1] | 20 | |
y'(x)=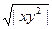 
| y(-1)=3 | [-1, 1] | 30 | |
| y'(x)=x+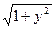
| y(-1)=1 | [-1, 1] | 40 | |
y'(x)=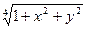 
| y(-1)=2 | [-1, 1] | 50 | |
y'(x)=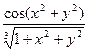 
| y(0)=3 | [0, π ] | 10 | |
| y'(x)=sin(x) ln(1+y2) | y(0)=1 | [0, π ] | 20 | |
| y'(x)=sin(y) cos(x+y2) | y(0)=2 | [0, π ] | 30 | |
| y'(x)=ex sin(y)+x2 ey | y(0)=3 | [0, π ] | 40 | |
| y'(x)= cos(x) (x+y2) | y(0)=1 | [0, π ] | 50 | |
y'(x)=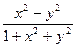 
| y(π /2)=2 | [π /2, π ] | 10 | |
| y'(x)=x 2y+y 2x | y(π /2)=1 | [π /2, π ] | 20 | |
| y'(x)= |x - y| cos(x2 + y2) | y(π /2)=3 | [π /2, π ] | 30 | |
y'(x)= 
| y(π /2)=2 | [π /2, π ] | 40 | |
| y'(x)=(y + x )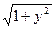
| y(π /2)=3 | [π /2, π ] | 50 |
Задача №2. Решить задачу Коши для дифференциального уравнения сведением к задачи Коши для системы уравнений первого порядка.
Табл.2.
| № варианта | Дифференциальное уравнение | Начальное условие | [x0, X] | N |
| y(x)=x y(x)+ sin(x) | y(0)=1, y'(0)=2 | [0, 2] | 10 | |
| y" '(x)=2x2 y(x) y" (x) | y(0)=2, y'(0)=2, y" (0)=1 | [0, 2] | 20 | |
| y" (x) – 3cos(x) y(x)=tg(x) | y(0)=3, y'(0)=2 | [0, 2] | 30 | |
| " 'y(x)=x y'(x) | y(0)=1, y'(0)=1, y" (0)=1 | [0, 2] | 40 | |
| y" '(x)=-cos(x) y" (x) – y(x) sin(x) | y(0)=2, y'(0)=2, y" (1)=1 | [0, 2] | 50 | |
| y" (x)– sin(x) y(x)=sin(x) | y(1)=3, y'(1)=1 | [1, 2] | 10 | |
| y" (x) – 2x2 y(x)=cos(x) | y(1)=1, y'(1)=1 | [1, 2] | 20 | |
| y" '(x)=(x – 1) y(x) + x y" (x) | y(1)=2, y'(1)=1, y" (1)=1 | [1, 2] | 30 | |
| y" (x) - sin(x) y(x)=sin3(x) | y(1)=3, y'(1)=1 | [1, 2] | 40 | |
| y" '(x)=x y(x) - sin(x) y'(x) | y(1)=1, y'(1)=1, y" (1)=1 | [1, 2] | 50 | |
| y" (x)-cos(x) y(x)=x | y(1)=2, y'(1)=1 | [1, 3] | 10 | |
| y" '(x) – 2x2 y(x)=x2 | y(1)=3, y'(0)=1, y" (0)=1 | [1, 3] | 20 | |
| y" (x) - lgx y(x)=2x | y(1)=1, y'(1)=1 | [1, 3] | 30 | |
| y" '(x) - 2|sin(x)| y'(x)=3x3 | y(1)=2, y'(1)=1, y" (1)=1 | [1, 3] | 40 | |
| y" (x) – 2lnx y(x)=1+x | y(1)=3, y'(1)=1 | [1, 3] | 50 | |
| y" '(x) - |cos(x)| y(x)=x | y(-1)=1, y'(-1)=1, y" (-1)=1 | [-1, 1] | 10 | |
| y" (x) - 2|x| y(x)=cos2(x) | y(-1)=2, y'(1)=1 | [-1, 1] | 20 | |
| y" '(x) - y(x)=e2x | y(-1)=3, y'(-1)=1, y" (-1)=1 | [-1, 1] | 30 | |
| y" (x) – ln(1+x2) y(x)=sin(2x) | y(-1)=1, y'(1)=1 | [-1, 1] | 40 | |
| y" '(x) – sin|x| y(x)=sin(x) | y(-1)=2, y'(-1)=1, y" (-1)=1 | [-1, 1] | 50 | |
| y" (x) - 2y(x)=sin(x) | y(0)=3, y'(0)=2 | [0, π ] | 10 | |
| y" '(x)=3y(x)+y" (x) cos(x) | y(0)=1, y'(0)=1, y" (0)=1 | [0, π ] | 20 | |
| y" (x) - 2x y(x)=x3 | y(0)=2, y'(0)=2 | [0, π ] | 30 | |
| y" '(x) - x y(x)=x4y'(x) | y(0)=3, y'(0)=1, y" (0)=1 | [0, π ] | 40 | |
| y" (x) - 2x2 y(x)=x2 | y(0)=1, y'(0)=2 | [0, π ] | 50 | |
| y" '(x)=cos(x) y(x)+ex y" (x) | y(2)=2, y'(2)=1, y" (2)=1 | [2, π ] | 10 | |
| y" (x) - 2x2 y(x)=2x ex | y(2)=3, y'(0)=2 | [2, π ] | 20 | |
| y" '(x) - 5y" (x)=32x | y(2)=1, y'(2)=1, y" (2)=1 | [2, π ] | 30 | |
| y" (x) - 2sin(x) y(x)=sin(3x) | y(2)=2, y'(0)=2 | [2, π ] | 40 | |
| y" '(x) - lnx y'(x)=1 | y(2)=3, y'(2)=1, y" (2)=1 | [2, π ] | 50 |
Задача №3.
Найти методом Рунге-Кутта с точностью ε = 10-8 решение задачи Коши y'(x)=2x(1+y2), y(0)=0 в точке x=1.
(Точным решением является функция y(x)=tg(x2))
Задача №4.
Решить методом Эйлера на отрезке [1, 2] задачу Коши
y'(x)=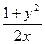 
, y(1)=0.
(Точным решением данной задачи является функция y(x)=tg(ln 
).
Контрольные вопросы:
1. Какое уравнение называется обыкновенным дифференциальным уравнением?
2. Какие методы решения задач для дифференциальных уравнений вы знаете?
3. В каком случае решение дифференциального уравнения единственно?
4. Рассказать правило Рунге для оценки погрешности.