Краевые задачи для обыкновенных дифференциальных уравнений

Лабораторная работа 2

Численные методы решения

обыкновенных дифференциальных уравнений (4 часа)

Краевые задачи для обыкновенных дифференциальных уравнений

Примерами краевых задач для обыкновенных дифференциальных уравнений являются следующие:

1) Найти функцию u(x), которая удовлетворяет на отрезке [a, b] уравнению

u" (x)=-f(x), (20)

а на концах отрезка условиям

u(a)=u(b)=0. (21)

Задача (20), (21) имеет следующее физическое состояние. Между точками x= a и x= b натянута упругая струна, находящаяся под действием внешней изгибающей нагрузки. f(x) – величина нагрузки, а u(x) – прогиб струны в безразмерных единицах.

2) Двухточечная краевая задача для линейного дифференциального уравнения второго порядка:

u" (x)+ p(x) u¢ (x)+ q(x) u(x)= f(x), (22)

α ₀ u(a)+ α ₁ u'(a)= A,

β ₀ u(b)+ β ₁ u'(b)= B. (23)

Рассмотрим частный случай задачи (22), (23):

u" (x)+ p(x) u(x)= f(x), x 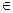[0, X], (24)

u(0)= a, u(X)= b. (25)

Введем сетку x_i= ih, i= 1, 2, …, N; h= X/N. Обозначим через u_i приближенное значение u(x) в узлах сетки. Рассмотрим уравнение (24) во внутренних узлах x_i, i= 1, 2, …, N-1 и заменим производную второго порядка разностной формулой

u" (x_i)= . (26)

Тогда из (24), (25) получим для определения u_i систему линейных уравнений

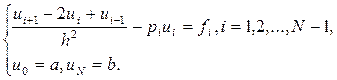(27)

Система (27) при p(x)≥ 0 имеет решение.

Система (27) представляет собой систему линейных уравнений с трехдиагональной матрицей

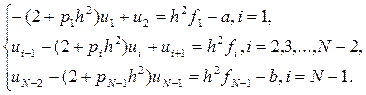(28)

и для ее решения применим метод прогонки, который фактически является методом исключения неизвестных Гаусса.

1. Прямой ход прогонки. Запишем первое уравнение (28) в виде

u₁= α ₁u₂ + β _1, α ₁= 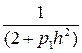, β ₁= 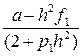. (29)

Подставив (29) во второе уравнение (28) и упростив выражения, увидим, что можно для u_i получить формулы

u_i= α _iu_i+1 + β _{i, ,}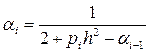

_, i= 2, …, N-2 (30)

Из последнего уравнения (28), учитывая (30) при i= N – 2, получим

u_N-1= β _N-1, α _N-1= 0, β _N-1= . (31)

2. Обратный ход прогонки. После вычисления прогоночных коэффициентов можно найти значения решения задачи. Формула (31) дает значение u_N-1:

u_N-1= β _N-1. (32)

Остальные значения вычисляем в обратном порядке:

u_i= α _iu_i+1 + β _i, , i= N-2, N-3, …, 2, 1. (33)

Рассмотрим метод пристрелки на примере решения линейной краевой задачи (24), (25). Если известны частное решение u(x) неоднородного уравнения u" (x)- p(x) u(x)= f(x) и два линейно независимых решения u₁(x), u₂(x) однородного уравнения u" (x) - p(x) u(x)= 0, то общее решение неоднородного дифференциального уравнения u" (x)- p(x) u(x)= f(x) можно записать в виде

u(x) + C₁u₁(x) + C₂u₂(x).

Постоянные C₁, C₂ можно определить из краевых условий (25).

В методе пристрелки используется следующий способ.

Сначала находят частное решение u(x) неоднородного уравнения u" (x)- p(x)u(x)= f(x), удовлетворяющее условию u(0)= a, и частное решение u₁(x) однородного уравнения u" (x) - p(x) u(x)= 0 удовлетворяющее условию u(0)=0.

Затем общее решение u(x) неоднородного уравнения u" (x)- p(x) u(x)= f(x), удовлетворяющее условию u(0)= a, записывают в виде u(x) + Cu₁(x). Остается найти постоянную С из условия u(x) + Cu₁(x)= b.

Приведем сеточный аналог метода пристрелки. Пусть краевая задача приведена к системе уравнений (27)

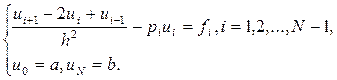(34)

Найдем частные решения неоднородной (35) и однородной (36) систем уравнений:

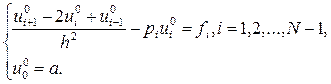(35)

(36)

Выбирая произвольные значения для 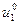, 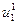(при этом должно быть 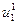≠ 0), находим из (35) и (36) формулы для вычисления частных решений:

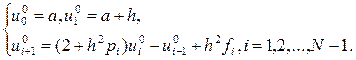(37)

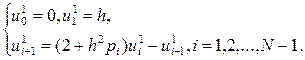(38)

Найдем С из условия 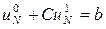и запишем решение:

(39)

(40)

Алгоритм метода пристрелки заключается в том, чтобы выбрать шаг h и выполнить последовательно вычисления по формулам (37) - (40).