
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекція 5. Симплекс-метод.
|
|
Суть вирішення будь-якої задачі лінійного програмування полягає у виборі з кінцевого числа припустимих базисних рішень системи обмежень такого рішення, на якому функція цілі приймає оптимальне значення. Геометрично це відповідає перебору всіх кутових крапок багатогранника рішень, утвореного перетином прямих ліній, побудованих за рівняннями системи обмежень.
Число припустимих базисних рішень, що перебираються, можна скоротити, якщо перебір робити не безладно, а з урахуванням змін лінійної функції цілі, тобто, щоб кожне наступне рішення було ближче до оптимального, ніж попереднє. Такий перебір дозволяє скоротити кількість кроків (ітерацій) при пошуку оптимуму цільової функції ОЗЛП.
Ідея послідовного поліпшення рішення лягла в основу універсального методу рішення задач ЛП - симплекс-методу (симплексного методу). Для реалізації симплексного методу – методу послідовного поліпшення рішення – необхідно задати:
1) спосіб визначення первинного припустимого базисного рішення;
2) правила переходу до кращого (не гіршого) рішення;
3) критерій перевірки оптимальності знайденого рішення.
Для використання симплекс-методу задача ЛП повинна бути зведена до ОЗЛП. Нехай у задачі ЛП є n змінних і m незалежних рівнянь обмежень. Виберемо k = n -m змінних у якості вільних. Тоді рівняння обмежень ОЗЛП можна записати в канонічному вигляді:
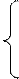
| a11 х1 + a12 х2+ … + a1k хk + b1 = S1 | |
| a21 х1 + a22 х2+ … + a2k хk + b2 = S2 | ||
| (4.1) | ||
| am1 х1 + am2 х2+ … + amk хk + bm = Sm |
Прирівняємо до 0 усі вільні змінні: х1= 0, х2= 0,... хk= 0. Тоді значення базисних змінних: S1 = b1, S2 = b2, … Sm = bm представляють первинне базисне рішення, що може бути або припустимим, або неприпустимим.
Рішення буде припустимим, якщо всі змінні (і вільні, і базисні) в отриманому рішенні невід’ємні. Якщо припустиме рішення вдається одержати одразу, то перший етап рішення задачі закінчується.
При переході до другого етапу рішення задачі аналізується значення цільової функції
W = c1 х1 + c2 х2+ … + ck хk для початкового базисного рішення. Якщо для даного базисного рішення у виразі для цільової функції W хоча б один з коефіцієнтів від’ємний
(ci < 0), то значення цільової функції можна зменшити, якщо відповідну змінну зробити відмінною від 0 (хi ≠ 0).
При цьому вільна змінна xi вважається базисною, а одна з базисних змінних Sj - вільною, тобто вільна і базисна змінні міняються місцями.
У тому випадку, коли у виразі для цільової функції W від’ємні коефіцієнти сi - відсутні, то рішення задачі завершується на першому етапі, тому що отримане базисне рішення є оптимальним.
При виборі базисних (основних) змінних на першому кроці можна скористатися таким правилом:
у якості базисних (основних) змінних на першому кроці варто вибрати, по можливості, такі m змінних, кожна з яких входить тільки в одне з m рівнянь системи обмежень, при цьому немає таких рівнянь системи, у які не входить жодна з цих змінних.
Основний алгоритм симплекса-методу.
Ітераційний процес при реалізації симплекс-методу складається з 4-х кроків.
Крок 1. Використовуючи стандартну (канонічну) форму запису ОЗЛП визначити початкове допустиме базисне рішення, прирівнюючи нулю k вільних змінних.
Крок 2. З числа вільних змінних вибирається змінна, що включається в новий базис, збільшення якої забезпечує поліпшення цільової функції W. Якщо такої змінної немає (ck > 0) рішення завершується. В іншому випадку здійснюється перехід до кроку 3.
Крок 3. З числа базисних перемінних S1,.. Sm вибирається виключна змінна, котра повинна прийняти нульове значення (стати вільною змінною).
Крок 4. Знаходиться нове базисне рішення, що відповідає новому складу вільних і базисних змінних. Після виконання кроку 4 алгоритм повторюється, починаючи з кроку 2.
Приклад.
Підприємство виробляє дві моделі продукції. Для виготовлення однієї моделі потрібно 3 одиниці сировини, а для іншої - 4 одиниці. Загальна кількість сировини, що витрачається протягом місяця, не повинне перевищувати 1700 одиниць. Для виготовлення 1-ої моделі потрібно 12 хв., для виготовлення другий - 30 хв. Середня кількість робочих днів у місяці – 20. Тривалість робочого дня – 8 годин. Виріб першого типу приносить 2 г.о. прибутку, другого - 4 г.о. прибутку.
Скільки виробів другої моделі необхідно випускати на місяць, щоб дістати максимальний прибуток.
Складаються рівняння обмежень:
- по затрачуваній сировині: 3 x1 + 4 х2 ≤ 1700;
- по витратах часу: 12 x1 + 30 х2 ≤ 20 х 8 х 60;
чи 2 x1 + 5 х2 ≤ 1600;
Цільова функція: W = 2 x1 + 5 х2 à максимум
чи W = - 2 x1 - 5 х2 à мінімум.
Приведемо задачу до ОЗЛП канонічного виду.
3 x1 + 4 х2 + S1 = 1700
2 x1 + 5 х2 + S2 = 1600
чи
S1 = 1700 - 3 x1 - 4 х2
S2 = 1600 - 2 x1 - 5 х2
Крок 1.1. Покладемо x1 = 0; x2 = 0. Тоді S1 = 1700; S2 = 1600. Отримане початкове базисне рішення є припустимим, тому що S1 і S2 > 0.
Проаналізуємо цільову функцію. Для обраного початкового базисного рішення W =0. Оскільки у виразі для цільової функції обидва коефіцієнти при вільних змінних менші нуля
(x1, x2 < 0), то рішення можна поліпшити, надавши одній із вільних змінних ненульове значення. Не рекомендується змінювати обидві вільні змінні одночасно.
Крок 2.1. Виберемо ту зі змінних, коефіцієнт при якій більше за модулем. Це змінна x2. Тоді, із системи обмежень ОЗЛП для S1 і S2 випливає; що при x1 = 0; x2 = 1700/4 = 425 і
x2 = 1600/5 = 320. З двох значень вибираємо мінімальне:
x2 = min{425, 320} = 320.
Визначаємо значення цільової функції W для x1 = 0; x2 = 320.
Одержимо W = - 2 x 0 – 4 x 320 = -1280. Крім того, S1 = 420, S2 = 0.
Крок 3.1. З числа базисних змінних вибираємо ту, котра повинна стати вільною. Нехай це буде базисна змінна з найменшим значенням, тобто S 2 = 1600. Вихідне рівняння, у якому буде виконуватися ця заміна, називається ведучим рівнянням. Формуємо нову систему рівнянь з нової вільної змінної S2. Нову систему можна сформувати, використовуючи, наприклад, стандартну процедуру виключення по методу Гаусса-Жордана.
Спочатку формується нове ведуче рівняння за правилом:
Новий ведучий рядок = (старий ведучий рядок): (ведучий елемент).
Ведучий елемент - це коефіцієнт при виключній змінній. Одержуємо:
| S2 | = | - | x1 -x2 | ||
Після цього формуємо інші рівняння, включаючи рівняння для цільової функції W. Як видно в новому ведучому рівнянні коефіцієнт при x2 = 1. Користуючись методом виключення, забезпечимо рівність нулю коефіцієнтів при x2 у всіх рівняннях системи, крім ведучого. Одержимо:
| x1 | + | х2 | + | S1 | + | S2 | = | ||||||
| x1 | + | х2 | + | S1 | + | S2 | = | х (-4) | |||||
| x1 | + | х2 | + | S1 | - | S2 | = | ||||||
Крок 4.1. Нова система рівнянь прийме такий вид:
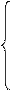
| x1 | + | х2 | + | S2 | = | ||||||
| x1 | + | S1 | - | S2 | = | |||||||
де x1, S2 - вільні змінні, x2, S1 - базисні змінні.
При x1 = 0 і S2 = 0: x2 = 320, S1 = 420, тобто є новим базисним рішенням.
З виразу для цільової функції виключимо нові базисні змінні.
| -2 | x1 | - | х2 | = | W | ||||||||
| x1 | + | х2 | + | S2 | = | х (-4) | |||||||
| - | x1 | + | S2 | = | W + 1280 | ||||||||
Отже одержали нове рівняння для цільової функції W. Повертаємося до кроку 2.
Крок 2.2. У виразі для цільової функції W, отриманому на попередньому кроці коефіцієнт при змінній x1 – від’ємний. Це означає, що якщо зробити змінну x1 базисною, то рішення можна поліпшити. Тому виконуємо наступну ітерацію, тобто приймаємо в якості базисної змінної змінну x1, а в якості вільної, замість x1 - S1. Ведуче рівняння:
| x1 | + | S1 | - | S2 | = | |||
Крок 3.2. Система рівнянь:
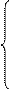 |
| x1 | + | S1 | - | S2 | = | |||||||
| - | х2 | + | S1 | - | S2 | = | - 500 | |||||
Крок 4.2. При S1, S2 = 0 одержуємо чергове базисне рішення: x1 = 300, x2 = 200. Використовуючи ведуче рівняння, одержуємо цільову функцію у вигляді:
| W | = | S1 | + | S2 | - 1400. | ||
Таким чином, останнє базисне рішення є оптимальним рішенням задачі.
Висновок. Симплекс-метод дозволяє одержати оптимальне рішення задачі за мінімальну кількість кроків.
Завдання. Перевірити отримане рішення графічним методом.