
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекція 6. Динамічне програмування.Розподілення капіталовкладень.
|
|
Динамічне програмування (ДП) – метод оптимізації, пристосований до операцій, у яких процес прийняття рішення може бути розбитий на етапи (кроки). Такі операції називаються багатокроковими.
Моделі лінійного програмування, розглянуті раніше, використовуються для прийняття великомасштабних (макроекономічних) рішень.
У великих економічних системах постійно потрібно приймати локальні (мікроекономічні) рішення. Моделі ДП цінні тим, що дозволяють на основі стандартного підходу при мінімальному втручанні людини приймати такі рішення. У тому випадку, якщо кожне окреме рішення не оцінюється як істотне, то в сукупності ці рішення можуть вплинути на підсумковий прибуток.
Моделі ДП застосовуються при рішенні таких задач:
- розробка правил управління запасами, що встановлюють момент поповнення запасів і розмір поповнюючого запасу;
- при розробці принципів календарного планування виробництва і вирівнювання зайнятості в умовах коливного попиту на продукцію;
- при розподілі дефіцитних капітальних вкладень між можливими новими напрямками їхнього використання;
- при складанні календарних планів поточного і капітального ремонту складного устаткування і його заміни;
- при розробці довгострокових правил заміни основних фондів, що вибувають з експлуатації (заміна устаткування);
- оптимізації маршрутів інформації й ін.
У загальному вигляді задачу ДП можна сформулювати в такому вигляді. Розглядається керований процес. У результаті керування система (об'єкт керування) S переводиться з початкового стану s0 у стан s’. Припустимо, що керування можна розбити на n кроків, тобто рішення приймається послідовно на кожному кроці, а керування, що переводить систему S з початкового стану в кінцевий являє собою сукупність n покрокових управлінь.
Позначимо через Хk керування на k- ому кроці (k =1, 2,... n). Змінні Хk задовольняють деяким обмеженням, тобто є припустимими. Нехай Х(Х1, Х2, … Хn) – керування, що переводить систему S зі стану s0 у стан s’. Позначимо через sk стан системи після k- го кроку керування. Одержимо послідовність станів s0, s1, … sk-1, sk, …, sn-1, sn = s’...
Показник ефективності розглянутої керованої операції – цільова функція – залежить від початкового стану і керування: Z = F(s0, X).
Задача покрокової оптимізації (задача ДП) формулюється так: визначити таке припустиме керування Х, що переводить систему S зі стану s0 у стан s’, при якому цільова функція приймає найбільше (найменше) значення.
Модель ДП. має такі особливості:
1. Задача оптимізації інтерпретується як n- кроковий процес керування.
2. Цільова функція дорівнює сумі цільових функцій кожного кроку.
3. Вибір керування на k- ому кроці залежить тільки від стану системи до цього кроку, не впливає на попередні кроки (немає зворотного зв'язку).
4. Стан sk після k- го кроку керування залежить тільки від попереднього стану sk-1 і керування Хk (відсутність післядії).
5. На кожному кроці керування Хk залежить від кінцевого числа керуючих перемінних, а стан sk – від кінцевого числа параметрів.
Замість загальної постановки задачі ДП із фіксованим числом кроків n і початковим станом s0 розглянемо послідовність задач задаючи послідовно n = 1, 2, … при різних s - однокрокову, двокрокову і т.ін. – використовуючи принцип оптимальності, сформульований Р. Беллманом у 1953 р.
Принцип оптимальності:
У будь-якому стані s системи в результаті деякого числа кроків, на найближчому кроці потрібно вибирати керування так, щоб воно в сукупності з оптимальним керуванням на всіх наступних кроках приводило до оптимального виграшу на всіх кроках, що залишилися, включаючи поточний. Даний принцип вірний, якщо процес керування – без зворотного зв'язку, тобто керування на даному кроці не повинне впливати на попередні кроки.
Уведемо деякі додаткові позначення.
На кожному кроці будь-якого стану системи sk-1 рішення Хk потрібно вибирати з урахуванням того, як цей вибір впливає на наступний стан sk і подальший процес керування, що залежить від sk, тому що це випливає з принципу оптимальності.
Однак є крок, останній, котрий можна планувати оптимально для будь-якого стану sn-1, виходячи тільки з міркувань цього кроку.
Розглянемо n -й крок: sn-1 - стан системи до початку n - го кроку, sn = s’ - кінцевий стан, Хn - керування на n -му кроці, fn(sn-1, Хn) - цільова функція (виграш) n - го кроку.
Відповідно до принципу оптимальності, Хn потрібно вибирати так, щоб для будь-яких станів sn-1 одержати максимум (мінімум) цільової функції на цьому кроці.
Позначимо через Z*n (sn-1) максимум цільової функції - показника ефективності n -го кроку за умови, що до початку останнього кроку система S була в довільному стані sn-1, а на останньому кроці керування було оптимальним.
Z*n (sn-1) називається умовним максимумом цільової функції на n -му кроці. Очевидно, що
Z*n (sn-1) = max fn(sn-1, Хn) (5.1)
{Хn}
Максимізація ведеться по всіх припустимих керуваннях Хn.
Рішення Хn, при якому досягається Z*n (sn-1), також залежить від sn-1 і називається умовним оптимальним керуванням на n -му кроці. Воно позначається через Х*n (sn-1).
Вирішивши одномірну задачу локальної оптимізації по рівнянню (5.1), знайдемо для всіх можливих станів sn-1 дві функції: Z*n (sn-1) і Х*n (sn-1).
Розглянемо тепер двокрокову задачу: приєднаємо до n -го кроку (n-1) -й.
Для будь-яких станів sn-2, довільних керувань Хn-1 і оптимальному керуванні на n -му кроці значення цільової функції на двох останніх кроках дорівнює:
fn-1(sn-2, Хn-1) + Z*n (sn-1) (5.2)
Відповідно до принципу оптимальності для будь-яких sn-2 рішення потрібно вибирати так, щоб воно разом з оптимальним керуванням на останньому (n -му) кроці приводило б до максимуму цільової функції на двох останніх кроках. Отже, потрібно знайти максимум виразу (5.2) по всіх припустимих керуваннях Хn-1. Максимум цієї суми залежить від sn-2, позначається через Z*n-1 (sn-2) і називається умовним максимумом цільової функції при оптимальному керуванні на двох останніх кроках. Відповідне керування Хn-1 на (n-1) -му кроці позначається через Х*n-1 (sn-2) і називається умовним оптимальним керуванням на (n-1) -му кроці.
Z*n-1 (sn-2) = max {fn-1 (sn-2, Хn-1) + Z*n (sn-1)} (5.3)
{Хn-1}
У результаті максимізації тільки за однією змінною відповідно до рівняння (5.3) знову виходять дві функції: Z*n-1 (sn-2) і Х*n-1 (sn-2).
Далі розглядається трикрокова задача: до двох останніх кроків приєднується
(n - 2) -й і т.д.
Позначимо через Z*k (sk-1) умовний максимум цільової функції, отриманої при оптимальному керуванні на n-k+1 кроках, починаючи з к -го до кінця, за умови, що до початку к -го кроку система знаходився в стані sk-1. Фактично ця функція дорівнює
n
Z*k (sk-1) = max ∑ fi (si-1, Хi)
{(xk, …xn)} i=k
Тоді
n
Z*k+1 (sk) = max ∑ fi (si-1, Хi)
{(xk+1, …xn)} i=k+1
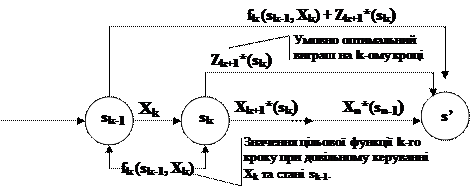 |
Мал. 5.1.
Цільова функція на n-k останніх кроках при довільному керуванні Хk на k -му кроці й оптимальному керуванні на наступних n-k кроках дорівнює
fk(sk-1, Хk) + Z*k+1 (sk)
Відповідно до принципу оптимальності, Хk вибирається з умови максимуму цієї суми на основі рекурентних співвідношень, що дозволяють знайти попереднє значення цільової функції, знаючи наступне тобто
Z*k (sk-1) = max {fk (sk-1, Хk) + Z*k+1 (sk)} (5.4)
{Хk}
k = n-1, n-2, … 2, 1.
Рівняння (5.4) називається рівнянням Беллмана.
Керування Хk на k-м кроці, при якому досягається максимум у (5.4), позначається через Х*k (sk-1) і називається умовним оптимальним керуванням на k -му кроці.
Якщо з (5.1) знайти Zn*(sn-1), то при k = n- 1 з (5.4) можна визначити вираз для
Zn-1*(sn-2) і відповідні Х*n-1 (sn-2) вирішивши задачу максимізації для всіх можливих значень sn-2. Після цього з Zn-1*(sn-2) з використанням (5.4) знаходяться рівняння станів.
Процес рішення рівнянь (5.1) і (5.4) називається умовною оптимізацією.
У результаті умовної оптимізації виходять дві послідовності.
1. Умовних максимумів цільової функції на останньому, на двох останніх, на …, на n кроках: