
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Елементи теорії ігор.
|
|
Основний постулат теорії ігор – будь-який суб'єкт системи – щонайменше так само розумний, як і сторона, що оперує, і робить усе можливе, щоб досягти своїх цілей. Від реального конфлікту гра (математична модель конфлікту) відрізняється тим, що вона ведеться за визначеними правилами, що встановлюють порядок і черговість дій суб'єктів системи, їх поінформованість, порядок обміну інформацією, формування результату гри.
Існує багато класів ігор, що відрізняються кількістю гравців, числом ходів, характером функцій виграшу і т.д. Виділимо такі основні класи ігор:
· антагоністичні (гри зі строгим суперництвом) і неантагоністичні. У першому випадку цілі гравців протилежні, у другому – можуть співпадати;
· стратегічні і нестратегічні (у перших суб'єкт системи діє незалежно від інших, переслідуючи свої цілі, у других – суб'єкти вибирають єдину для всіх стратегію);
· парні ігри й ігри для N- осіб;
· коаліційні і безкоаліційні;
· кооперативні і некооперативні (у перших можливий обмін інформацією про можливі стратегії гравців);
· кінцеві і нескінченні (у перших – кінцеве число стратегій).
Найбільше поширення на практиці мають парні стратегічні безкоаліційні кінцеві некооперативні ігри. Модель проблемної ситуації в цьому випадку має вигляд:
< U, V, W1, W2, R1, R2 >,
де U – множина стратегій сторони, що оперує, (конструктора);
V – множина стратегій сторони, що опонує, (технолог і природа);
W1 і W2 – показники якості гравців;
R1 і R2 – системи переваг гравців.
Системи переваг гравців, у свою чергу, ґрунтуються на двох провівдних принципах раціонального поводження: принципі найбільшого гарантованого результату і принципі рівноваги.
Перший грунтується на тому, що раціональним вибором одного з гравців повинен вважатися такий, при якому він розраховує на найнесприятливішу для нього реакцію з боку іншого гравця.
Другий принцип говорить, що раціональним вибором будь-якого гравця вважається така стратегія u$ (чи v$), для якої ситуація (u$, v$) взаємовигідна: будь-яке відхилення від даної ситуації гри не є вигідним ні для одного з гравців.
Вирішується парна матрична гра з нульовою сумою (виграш однієї сторони дорівнює програшу іншої) на основі розгляду платіжної матриці, що являє собою сукупність значень U і V (пари стратегій (u, v) U ´ V називається ситуацією гри) а також виграшів Wij при парному сполученні всіх можливих стратегій сторін.
Рішення парної матричної гри може бути в чистих стратегіях, коли для кожної зі сторін може бути визначена єдина оптимальна стратегія, відхилення від який невигідно обом гравцям. Якщо вигідно використовувати кілька стратегій з визначеною частотою їхнього чергування, то рішення знаходиться в змішаних стратегіях.
Основні особливості використання методів теорії полягають у наступному. Як можливі стратегії з боку проектованої системи розглядаються можливі варіанти її побудови, з яких варто вибрати найбільш раціональний. Як стратегії супротивника розглядаються можливі варіанти його протидії, стратегії їхнього застосування.
Необхідно відзначити, що при розгляді ігор з використанням адаптивної системи число її стратегій може бути істотно розширене завдяки реалізації " гнучких" рішень. Аналіз ігрових ситуацій у цьому випадку може бути спрямований не тільки на вибір раціонального варіанта проектованої системи, але і на визначення алгоритмів раціонального застосування системи в конфліктній ситуації.
Інша особливість застосування методів теорії ігор полягає у виборі рішень, одержуваних на основі аналізу конфліктної ситуації. У теорії ігор доводиться теорема про те, що оптимальна стратегія для кожного з гравців є оптимальною і для іншого. Так, якщо рішення гри отримане в чистих стратегіях (є сідлова точка), то вибір рішення однозначний. Наприклад, якщо для парної антагоністичної гри 3´ 4 скласти матрицю, де елементами uij будуть виграші (програші) гравців, то сідлова точка знаходиться на перетині максиміну рядків і мінімаксу стовпців.
Оптимальними стратегіями гри наведеної в табл. 8.1 будуть для A – 2, для B – 2. Ціна гри дорівнює 5. Відзначимо, що у випадку наявності сідлової точки жоден із гравців не може поліпшити стратегію, і стратегії такі називаються чистими. Відзначимо, що гра з чистими стратегіями може існувати тільки при наявності повної інформації про дії супротивника.
Таблиця 8.1
| Стратегії A | Стратегії B | min рядків | |||
| -4 | -4 | ||||
| max стовпців |
Якщо ж рішення гри отримане в змішаних стратегіях, то це еквівалентно створенню безлічі варіантів проектованого компонента і використанню їх з оптимальними частотам, що відповідають оптимальній змішаній стратегії. У випадках, коли немає повної інформації про дії супротивника, вводяться імовірності застосування тієї чи іншої стратегії у вигляді векторів
| P< n> =< p1, p2,..., pn> - для гравця A, де | 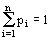
| ; |
| Q< m> =< q1, q2,..., qn> - для гравця B, де | 
| . |
При цьому гравець A вибирає стратегію відповідно до принципу максиміну за виразом:
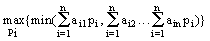
а гравець B за принципом мінімаксу
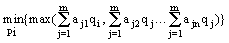
Розглянемо приклад: нехай розглядається прийняття рішення в грі 2´ 2, де гравець A знає імовірність стратегії 1, тобто p1, тоді очевидно імовірність стратегії 2 буде 1- p, відповідно стратегії гравця B будуть q1 і 1-q1. Платіжна матриця буде мати вигляд:
| B | (8.1) | |||
| q1 | 1-q1 | |||
| A | p1 | a11 | a12 | |
| 1-p1 | a21 | a22 |
На підставі матриці (8.1) і наведених вище виразів складається таблиця:
Таблиця 8.2
| Чисті стратегії гравця В | Очікувані виграші гравця А |
| (a11-a21)p1 + a21 | |
| (a12-a22)p1 + a22 |
З табл. 8.2 видно, що очікуваний виграш гравця A лінійно залежить від імовірності p1 (у даному випадку задача може бути вирішена графоаналітично). Тоді змішана стратегія гравця А буде мати вид
< p*1, p*2>,
тобто гравцю A вигідно застосовувати стратегію 1 з частотою (імовірністю) – p1, а стратегію 2 з частотою p2.
Очевидно, що розробка декількох варіантів поведінки пов’язана з великими витратами, не завжди може бути реалізована й ускладнює використання системи. Тому при одержанні рішення в змішаних стратегіях рекомендуються такі випадки прийняття остаточного рішення:
· для подальшого застосування вибирається той варіант, що гарантує максимальну якість (вибір за максимінною стратегією аналогічно критерію Вальда);
· вибирається той варіант, що у змішаній стратегії повинен використовуватися з максимальною імовірністю;
· реалізується кілька варіантів поведінки з частотами, що відповідають змішаній стратегії (створення адаптивно-модульних конструкцій).
Важливе значення в задачах дослідження якості адаптивних систем має не тільки рішення гри, але й аналіз платіжної матриці. Це особливо важливо в тих випадках, коли рішення в змішаних стратегіях не реалізується. Цей аналіз може проводитися на основі:
- оцінки можливих втрат ефективності у випадку реалізації чистої стратегії;
- визначення додаткових витрат на їхню компенсацію за допомогою " гнучких" рішень;
- оцінки імовірності розглянутих стратегій протидії;
- визначення можливості реалізації компромісних варіантів і т.ін.
Для аналізу конфліктної ситуації потрібно на основі математичної моделі операції побудувати платіжну матрицю [Wmn] = [Wij], де Wij характеризує якість вибору при виборі
i- го варіанта реалізації і при j- му варіанті протидії супротивника.
Рішення може бути отримане в чистих стратегіях, коли є сідлова точка. Умова сідлової точки має вигляд
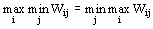
| (8.2) |
де ліва частина виразу – нижня ціна гри, права – верхня ціна гри.
Якщо умова
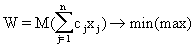
де М – математичне очікування – не виконується, то сідлова точка відсутня і потрібна реалізація змішаної стратегії.
Рішення в змішаних стратегіях полягає в реалізації чистих стратегій з різними імовірностями, що задаються розподілом:
для шуканого вибору – у в идгляі вектора-стовпця
| G = {gi}, де i = 1, 2...m; | 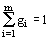
| ; |
для протидії – у вигляді вектора-рядка
| F = {fj}, де j = 1, 2...n; | 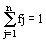
| , |
де gi – імовірність вибору стратегії ui;
fj – імовірність вибору стратегії vj.
Платіжну функцію запишемо в токому вигляді:
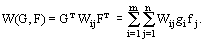
де індексом " т" позначена процедура транспонування.
Платіжна функція W(G, F) завжди має сідлову точку, тобто завжди існує рішення матричної гри. Це твердження відповідає основній теоремі теорії матричних ігор: кожна матрична гра з нульовою сумою має, принаймні, одне рішення в чистих чи змішаних стратегіях.
Послідовність вирішення гри така:
1. Аналізується платіжна матриця на предмет виключення свідомо невигідних і дублюючих стратегій.
2. Перевіряється наявність сідлової точки за умовою (8.2).
3. Якщо рішення в чистих стратегіях відсутнє, то шукається рішення в змішаних стратегіях за допомогою методів лінійного програмування або методом Монте-Карло.
У співвідношенні стратегії і результатів в задачах прийняття рішень можливі три ситуації, які суттєво визначають моделі і процедуру рішення.
1. Визначеність. Кожна альтернатива приводить до єдиного рішення (усі розглянуті раніше задачі відносяться до цього класу).
2. Характеризуються наявністю ризику – кожна альтернатива приводить до безлічі результатів. Відомі імовірності появи результатів. Для рішення задач з ризиком використовується оптимізація в середньому. У якості найкращої вибирається така стратегія, що перетворює в максимум математичне очікування показника ефективності.
3. Найбільш складні задачі – це задачі, що вирішуються в умовах невизначеності. У таких задачах відомий набір результатів, але не відомі імовірності їхньої появи. Для рішення задач в умовах невизначеності використовуються спеціальні критерії: Вальда, Севіджа, Гурвіца.
Питання до курсу