
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа 2. Формат А3. Выполнить три задачи на пересечение поверхности плоскостью и прямой. Пример выполнения листа - на рис. 7
|
|
Лист 7
Формат А3. Выполнить три задачи на пересечение поверхности плоскостью и прямой.Пример выполнения листа - на рис.7. Задачи 1 и 2 выполняют в левой части листа (одна под другой), а задачу 3— на правой части листа.
Задача 1. Д а н о: пирамида и прямая l. Т р е б у е т с я: определить точки пересечения прямой l с поверхностью трехгранной пирамиды. Все варианты задач имеют два одинаковых параметра: высоту пирамиды - 70 мм и диаметр вспомогательной окружности - 60 мм, в которую вписывается треугольное основание произвольного расположения по усмотрению студента. Положение прямой общего положения, которая пересекает пирамиду, устанавливается студентом также самостоятельно.
Указания к выполнению задачи 1. Чтобы решить задачу, необходимо: 1) заключить прямую во вспомогательную плоскость частного положения (фронтально-проецирующую или горизонтально-проецирующую); 2) построить линию пересечения пирамиды с этой вспомогательной плоскостью; 3) отметить точки пересечения проекций прямой с проекциями линии пересечения; 4) определить видимость.
Так как плоскость, в которую заключается прямая, частного положения, то одна из проекций фигуры сечения пирамиды совпадает с проекцией секущей плоскости, выродившейся в линию. Вторую проекцию сече-
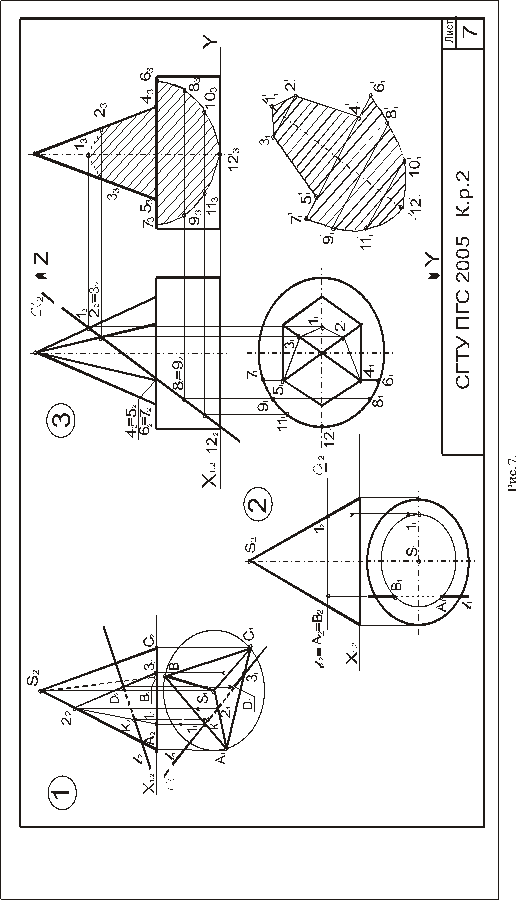
ния достраивают по точкам фигуры сечения, которые лежат непосредственно на ребрах. Задача может иметь одно из трех решений: прямая пересекает пирамиду в двух точках, в одной точке (касается) и не пересекает поверхность.
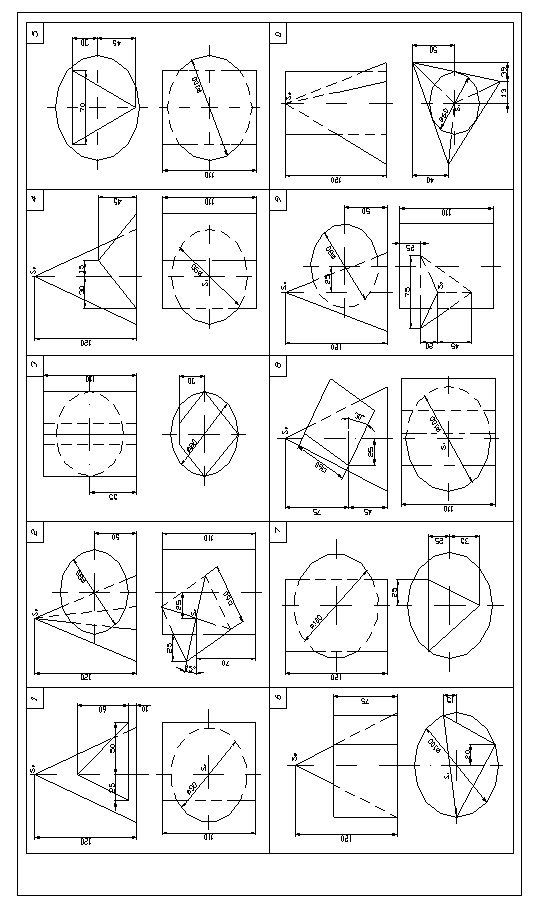
Задача 2. Д а н о: основание конуса — окружность диаметром 60 мм, высота конуса - 70 мм; прямая l. Т р е б у е т с я: определить точки пересечения прямой l с поверхностью прямого кругового конуса. Положение прямой студент выбирает самостоятельно, учитывая характеристику прямой, указанную в табл.5.
Таблица 5
| Номер варианта | Характеристика прямой l |
| Нисходящая общего положения | |
| Фронтальная под углом к П1 45° | |
| Горизонтально-проецирующая | |
| Горизонтальная под углом к П2 30° | |
| Фронтально-проецирующая | |
| Восходящая общего положения | |
| Горизонтальная под углом к П2 45° | |
| Фронтально-проецирующая |
Указания к выполнению задачи 2. Чтобы решить задачу, необходимо выполнить действия, аналогичные перечисленным в указаниях к задаче 1. При этом следует напомнить, что выбирать нужно такие вспомогательно-секущие плоскости, которые дают наипростейший контур сечения конуса: окружность и треугольник. Так, например, для задачи 2, помещенной на рис.7, вспомогательная секущая плоскость является горизонтально-проецирующей. Такая плоскость дает сечение в виде треугольника. После определения точек пересечения прямой с конусом не забудьте установить видимые отрезки прямой.
Задача 3. Построить три проекции линии пересечения сложной поверхности с фронтально-проецирующей плоскостью и способом совмещения (вращения вокруг линии уровня) определить натуральную величину этого сечения. Данные для вычерчивания комбинированной поверхности берут из табл. 6.
Указания к выполнению задачи 3. Задачу размещают на правой стороне листа (см. рис.7).Высота всей комбинированной поверхности равна 100 мм, нижняя ее часть — 35 мм. Размеры диаметров оснований поверхностей и вспомогательных окружностей, а также стороны многоугольников приведены в табл. 6. Положение секущей плоскости для своего варианта берется из табл. 6. Задачу решают в два этапа: 1) строят проекции сечения; 2) определяют натуральную величину сечения указанным способом.
Так как в данном задании для пересечения предложена плоскость частного положения: фронтально-проецирующая, то решение задачи сводится к построению проекций ряда точек фигуры сечения заданной поверхности как точек, расположенных на образующих или направляющих линиях этой поверхности. Первоначально крайние и промежуточные точки сечения назначаются на следе секущей плоскости. Натуральную величину сечения определяют по тем же точкам, которые были установленына первом этапе. За ось вращения плоскости сечения выбирают фронталь плоскости сечения, совпадающую с его осью симметрии. Для того чтобы избежать наложения изображений, фронталь следует размещать на свободном поле чертежа параллельно следу секущей плоскости. Каждая точка сечения будет вращаться вокруг оси в плоскости, перпендикулярной ей. Радиус вращения отображен в натуральную величину на горизонтальной плоскости проекций и соответствует расстоянию от точки до продольной оси симметрии (оси вращения).

Лист 8
Формат А3. Выполнить две задачи на пересечение многогранных и кривых поверхностей и построение разверток поверхностей. Пример выполнения приведен на рис. 8.
Задача 1. Д а н о: многогранник и кривая поверхность. Т р е б у е т с я: способом вспомогательно-секущих плоскостей построить линию пересечения многогранной и кривой поверхностей, выделив ее видимые и невидимые участки. Данные для задачи берут из табл. 7.
Указания к выполнению задачи 1. Задачу выполняют на левой половине листа в такой последовательности: 1) намечают расположение вспомогательных секущих плоскостей частного положения (уровня) или проецирующих; 2) с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей; 3) полученные точки соединяют плавными кривыми или прямыми линиями, установив предварительно последовательность расположения точек на линии пересечения поверхностей. Видимую часть линий контура, в том числе и линии пересечения, обводят сплошной основной, а невидимую—штриховой линиями. При решении задач на взаимное пересечение поверхностей следует помнить следующие положения.
1. Чтобы построить точку, принадлежащую линии пересечения поверхностей, нужно обе поверхности рассечь вспомогательной плоскостью (иногда вспомогательной поверхностью) и, найдя линии пересечения вспомогательной плоскости с заданными поверхностями, отметить общие для них точки. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Использование нескольких вспомогательных плоскостей позволяет определить ряд точек линий пересечения. Соединять можно только те точки, которые расположены в одной грани многогранника.
2. Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения поверхностей становится известной без дополнительных построений: она совпадает с проекцией поверхности.
3. Если линия, принадлежащая поверхности, видна не полностью, то точки перехода от видимой части линии пересечения к невидимой располагаются на очерке поверхности. Видимая часть линии пересечения поверхностей должна быть видимой как на одной поверхности, отдельно взятой, так и на другой.
4. Чтобы найти верхнюю или нижнюю точку линии пересечения, соответствующей грани с конусом, нужно взять такую вспомогательную плоскость, которая должна проходить через вершину конуса перпендикулярно
этой грани призмы. (Для прямой призмы - перпендикулярно ребрам основания.)
Задача 2. Д а н о: две пересекающиеся поверхности - многогранник и кривая поверхность - и линия их пересечения. Т р е б у е т с я: построить полную развертку одной из пересекающихся поверхностей и нанести на ней линию их пересечения. Поверхность для построения развертки студент выбирает сам из двух поверхностей задачи 1 в соответствии со своим вариантом. Линия пересечения поверхностей наносится по результату решения задачи 1.
Указания к выполнению задачи 2. Задачу выполняют на правой половине листа в такой последовательности: 1) в кривую поверхность вписывают многогранник; 2) определяют натуральные величины всех ребер вписанного многогранника; 3) на плоскости чертежа строят одну из граней поверхности по ее натуральным величинам ребер и к ней последовательно пристраивают остальные грани, пользуясь смежными ребрами; 4) соответствующие вершины граней соединяют плавными кривыми линиями.
При развертывании многогранной поверхности выполняют только вторую и третью операции. Линия пересечения поверхностей наносится на развертку с помощью ее характерных точек. Для каждой такой точки в ортогональных проекциях определяют положение образующей и направляющей линий поверхности, на пересечении которых расположена взятая точка. Строят эти линии (образующую и направляющую) на развертке и в их пересечении отмечают искомую точку линии пересечения поверхностей (рис. 8).
Лист 9
Формат А 4. Выполнить задачу на построение линии пересечения поверхностей. Пример выполнения листа представлен на рис.9.
Задача 1. Д а н о: две пересекающиеся кривые поверхности. Т р е б у е т- с я: способом вспомогательных секущих плоскостей построить линию их пересечения, выделив ее видимые и невидимые участки. Данные варианта задачи берут из табл.8.
Указания к выполнению задачи 1. Задачу выполняют в такой последовательности: 1) определяют точки пересечения очерковых образующих одной поверхности с другой, затем второй поверхности с первой; 2) определяют наивысшие и наинизшие точки линии пересечения; 3) определяют промежуточные точки линии пересечения; 4) все найденные точки пересечения последовательно соединяют кривой линией, учитывая их видимость.
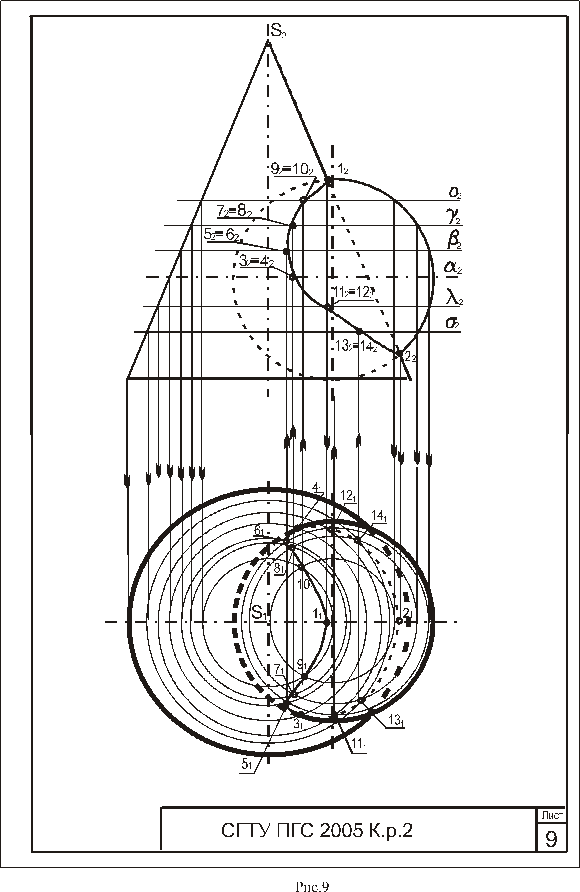


При выборе вспомогательных секущих плоскостей необходимо помнить, что они должны пересечь одновременно обе поверхности и дать наипростейшие фигуры сечения. Для всех вариантов заданий вспомогательными секущими плоскостями могут быть выбраны плоскости уровня: для одних - горизонтальные, для других - вертикальные или те и другие. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательной секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения самой секущей плоскости.