Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование рациональных дробей
|
|
1. Интегрирование простейших дробей. Рациональной дробью называется дробь вида P(x)/Q(x), где Р (х) и Q (х) — многочлены. Рациональная дробь называется правильной, если степень многочлена Р (х) ниже степени многочлена Q (х); в противном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
I. 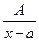 ;
;
II.  , где т — целое число, большее единицы;
, где т — целое число, большее единицы;
III. 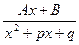 , где
, где  < 0 т. е. квадратный трехчлен x2 + px+q не имеет действительных корней;
< 0 т. е. квадратный трехчлен x2 + px+q не имеет действительных корней;
IV. 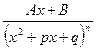 , где n - целое число, большее единицы, и квадратный трехчлен х2+рх+q не имеет действительных корней.
, где n - целое число, большее единицы, и квадратный трехчлен х2+рх+q не имеет действительных корней.
Во всех четырех случаях предполагается, что А, В, р, q, a — действительные числа. Перечисленные дроби будем соответственно называть простейшими дробями I, II, III и IV типов.
Рассмотрим интегралы от простейших дробей первых трех типов. Имеем
I. 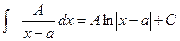
II. 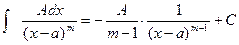
III. 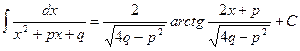
Действительно, для этого частного случая простейшей дроби III типа получаем
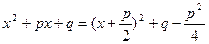 ИЛИ
ИЛИ 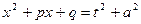
где 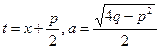 (здесь
(здесь  < 0), откуда
< 0), откуда
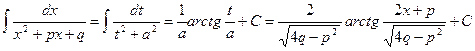
1403. Найти интеграл 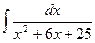
Решение.
Имеем
 ▲
▲
1404. Найти интеграл 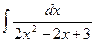
Решение.
Имеем
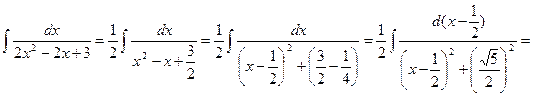
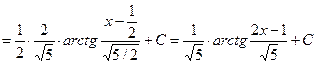
Покажем, как интегрируются в общем виде простейшие дроби III типа.
Требуется найти 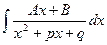 ,
,  < 0. Выделим в числителе дроби производную знаменателя. Для этого числитель представим в виде
< 0. Выделим в числителе дроби производную знаменателя. Для этого числитель представим в виде
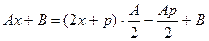
Тогда
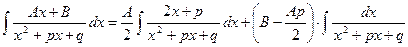
В первом интеграле числитель является производной знаменателя; поэтому так как x2+рх+q> 0 для любого значения х. Второй интеграл, как уже было отмечено, находится по формуле

Итак,
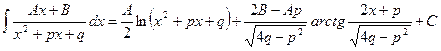
1405. Найти интеграл 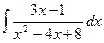
Решение.
Имеем
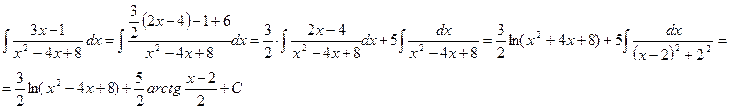 ▲
▲
1406. Найти интеграл 
Решение.
Имеем
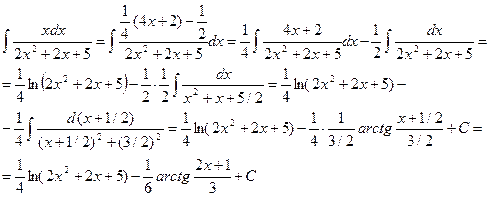
▲
1407. Найти интеграл 
Решение.
Предварительно в этом интеграле произведем замену переменной х2=t, тогда 2xdx = dt, xdx=(l/2)dt. Следовательно,

▲
Рассмотрим теперь частный случай интеграла от простейшей дроби IV типа. Для интеграла 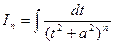 (n — целое положительное число) имеет место следующая рекуррентная формула:
(n — целое положительное число) имеет место следующая рекуррентная формула:
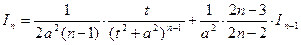
Эта формула позволяет после (n - 1)-кратного применения свести данный
интеграл In к табличному интегралу 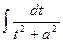
1408. Найти интеграл 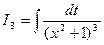
Решение.
Здесь п = 3. После первого применения рекуррентной формулы получаем
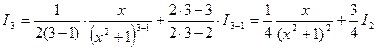
К интегралу 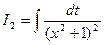 снова применяем рекуррентную формулу (здесь полагаем n = 2):
снова применяем рекуррентную формулу (здесь полагаем n = 2):

Итак,
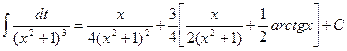
Окончательно имеем

▲
____________
Покажем теперь в общем виде, как интегрируются простейшие дроби IV типа. Требуется найти 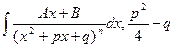 < 0.
< 0.
Выделим в числителе производную от квадратного трехчлена, стоящего в знаменателе:
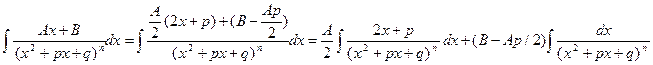
Первый интеграл в правой части равенства легко находится при помощи подстановки 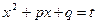 , авторой преобразуем так:
, авторой преобразуем так:
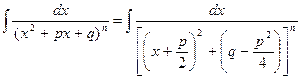
Полагая теперь 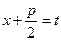 , dx = dt и обозначая
, dx = dt и обозначая 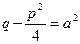 , получаем
, получаем
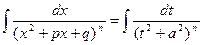
Таким образом, интегрирование элементарной дроби IV типа может быть выполнено при помощи рекуррентной формулы.
1409. Найти интеграл 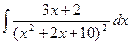
Решение.
Имеем

В первом интеграле произведем замену 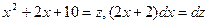 , а во втором интеграле положим
, а во втором интеграле положим 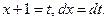 Отсюда
Отсюда

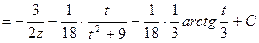
Возвращаясь к старой переменной, получаем
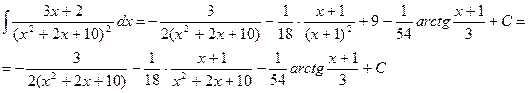
▲
Найти интегралы:
1410.  1411.
1411. 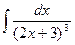 1412.
1412. 
1413. 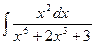 1414.
1414.  1415.
1415. 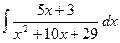
1416.  1417.
1417. 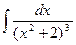 1418.
1418. 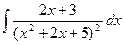
2. Интегрирование рациональных дробей с помощью разложения иа простейшие дроби. Перед интегрированием рациональной дроби Р (x)/Q (x) надо сделать следующие алгебраические преобразования и вычисления:
1) если дана неправильная рациональная дробь, то выделить из нее целую часть, т. е. представить в виде

где М (х) — многочлен, а P1 (x)/Q (x) —правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
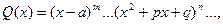
где  < 0, т. е. трехчлен x2+px+q имеет комплексные сопряженные корни;
< 0, т. е. трехчлен x2+px+q имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби

4) вычислить неопределенные коэффициенты A1, А2,..., Ат,..., B1, C1, B2, С2,..., Вn, Сn,..., для чего принести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения. Часто бывает полезно комбинировать оба способа вычисления коэффициентов.
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.
С л у ч а й 1. Знаменатель имеет только действительные различные корни, т. е. разлагается на неповторяющиеся множители первой степени.
1419. Найти интеграл 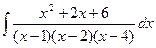 .
.
Решение.
Так как каждый из двучленов х —1, х —2, х —4 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:

Освобождаясь от знаменателей, получим
 . (*)
. (*)
Следовательно,

Сгруппируем члены с одинаковыми степенями:
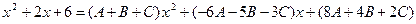
Сравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений
 ,
,
из которой найдем А = 3, В = - 7, С = 5.
Итак, разложение рациональной дроби на простейшие имеет вид
Неизвестные A, В, С в разложении можно было определить и иначе. После освобождения от знаменателя можно придать х столько частных значений, сколько содержится в системе неизвестных, в данном случае—три частных значения.
Особенно удобно придавать х значения, являющиеся действительными корнями знаменателя. Применим этот прием к решению данного примера. После освобождения от знаменателя мы получили равенство (*). Действительными корнями знаменателя являются числа 1, 2 и 4. Положим в этом равенстве х=1, тогда
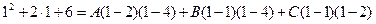
откуда 9 = 3A, т. е. A = 3. Полагая х = 2, получаем 14= - 2В, т. е. В = - 7; полагая х = 4, имеем 30 = 6С, т. е. С = 5. В результате получились те же значения, что и при первом способе определения неизвестных. Таким образом,
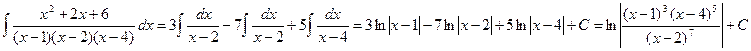 ▲
▲
_____________
С л у ч а й 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т. е. знаменатель разлагается на множители первой степени и некоторые из них повторяются.
1420. Найти интеграл 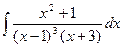
Решение.
Множителю (х—1)3 соответствует сумма трех простейших дробей 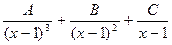 , a множителю x+З — простейшая дробь
, a множителю x+З — простейшая дробь 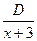 . Итак,
. Итак,
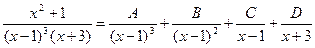
Освободимся от знаменателя:
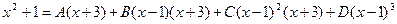
Действительными корнями знаменателя являются числа 1 и — 3. Полагая x=1, получаем 2 = 4A, т. е. A =1/2. При х =- 3 имеем 10 = — 64D, т. с. D = — 5/32.
Сравним теперь коэффициенты при старшей степени х, т. е. при х3. В левой части нет члена с х3, т. е. коэффициент при х3 равен 0. В правой части коэффициент при х3 равен C + D. Итак, C + D = 0, откуда С = 5/32.
Остается определить коэффициент В. Для этого необходимо иметь еще одно уравнение. Это уравнение можно получить путем сравнения коэффициентов при одинаковых степенях х (например, при х2) или придав х какое-нибудь численное значение. Удобнее взять такое значение, при котором вычислений будет возможно меньше. Полагая, например, х = 0, получаем
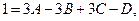 или
или  т. е.
т. е. 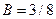
Окончательное разложение данной дроби на простейшие имеет вид

Таким образом, получим
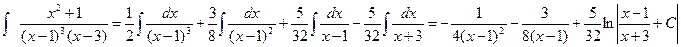
▲
С л у ч а й 3. Среди корней знаменателя имеются простые комплексные корни, т. е. разложение знаменателя содержит квадратичные неповторяющиеся множители.
1421. Найти интеграл 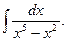
Решение.
Разложим знаменатель на множители:
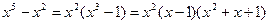
Тогда

Освобождаемся от знаменателя:

Действительными корнями знаменателя являются числа 0 и 1. При х = 0 имеем 1= — А, т. е. А = — 1. При x=1 имеем 1=3С, т. е. С=1/3. Перепишем предыдущее равенство в виде
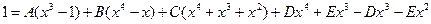
Сравнивая коэффициенты при х4, х3, х2, получаем систему уравнений
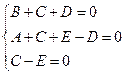
из которой найдем: В = 0, D = — 1/3, E=1/3. Итак,

Следовательно,

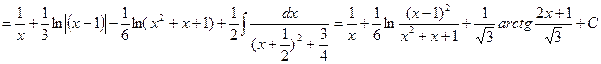
▲
С л у ч а й 4. Среди корней знаменателя имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.
1422. Найти интеграл  .
.
Решение.
Так как х2 + 1 есть двукратный множитель, то
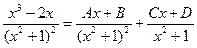
Освобождаясь от знаменателей, получим
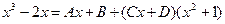
Приравняем коэффициенты при одинаковых степенях х:
| x3 | 1=C |
| х2 | 0=D |
| x | -2=A+C; A=-3 |
| x0 | 0=B+D; B=0 |
Следовательно,
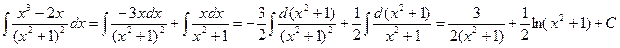
Заметим, что данный интеграл можно было найти проще с помощью подстановки х2 +1= t. ▲
1423. Найти интеграл 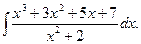
Решение.
Выделим целую часть данной неправильной рациональной дроби:
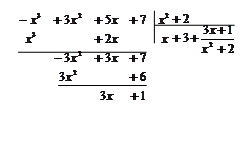 |
Итак,
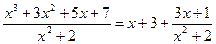
Отсюда находим

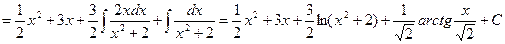 ▲
▲
1424. Найти интеграл 
Решение.
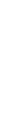 Так как подынтегральная функция является правильной дробью, то ее следует сразу представить в виде суммы простейших дробей. Легко видеть, что многочлен х3 + 6х2+11х+6 обращается в нуль при х = —1, поэтому он делится без остатка на х+1. Выполним деление:
Так как подынтегральная функция является правильной дробью, то ее следует сразу представить в виде суммы простейших дробей. Легко видеть, что многочлен х3 + 6х2+11х+6 обращается в нуль при х = —1, поэтому он делится без остатка на х+1. Выполним деление:




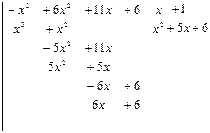
Следовательно,


Освобождаясь от знаменателей, получим
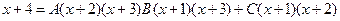
Полагая х=-1, найдем 3=2А, т. е. А = 3/2. Если х= — 2, то получим 2=- В, т. е. В=-2. При х =-3 получим 1=2С, т. е. С=1/2. Итак,
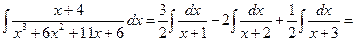
 ▲
▲
1425. Найти интеграл 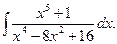
Решение.
Прежде всего нужно выделить целую часть:

|

 | |||||
 | |||||
 |
Следовательно,
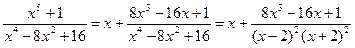
Разложим теперь правильную дробь на простейшие:

Освободимся от знаменателей:
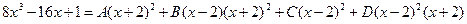
Полагая х=2, найдем 33=16А, т. е. А = 33/16. При х = — 2 получим — 31 = 16С, т.е. С=— 31/16. Если х = 0, то 1==4А — 8B + 4C + 8D. Заменив А и С их значениями, получаем
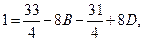 или
или 
Для того чтобы найти В и D, составим еще одно уравнение. Сравнив коэффициенты при х3, получим 8 = B + D. Решив систему уравнений
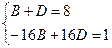
находим D= 129/32, B= 127/32.
Итак,

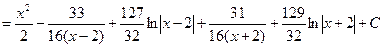 ▲
▲
1426. Найти интеграл  .
.
Решение.
Подынтегральная функция является правильной рациональной дробью и можно было бы найти интеграл, представив эту дробь в виде суммы простейших дробей. Однако нахождение интеграла можно значительно упростить, если произвести замену переменной х— 1=t; тогда x = t+1 и dx = dt. В результате получаем

▲
1427. Найти интеграл 
Решение. Преобразуем знаменатель:  =
= 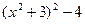 Теперь имеем
Теперь имеем
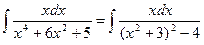
Произведем замену x2 + 3 = t тогда 2х dx = dt и
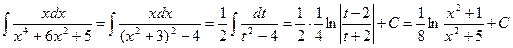
Из последних двух примеров видим, что иногда перед интегрированием рациональной дроби следует произвести замену переменной. ▲
Найти интегралы:
1428. 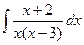 1429.
1429. 
1430. 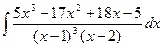 1431.
1431. 
1432. 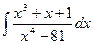 1433.
1433. 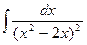
1434. 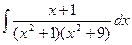 1435.
1435. 
1436. 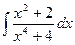 1437.
1437. 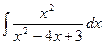
Указание: представить знаменатель в виде 
1438.  1439.
1439. 
1440. 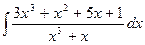
3. Интегралы вида 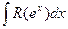 , где R – рациональная функция. С помощью подстановки
, где R – рациональная функция. С помощью подстановки  =t, откуда
=t, откуда  dx=dt, dx=dt/
dx=dt, dx=dt/  =dt/t, интеграл указанного вида преобразуется в интеграл от рациональной функции
=dt/t, интеграл указанного вида преобразуется в интеграл от рациональной функции
1441. Найти интеграл 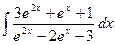
Решение: положим  =t; тогда
=t; тогда  dx=dt, dx=dt/t, откуда
dx=dt, dx=dt/t, откуда
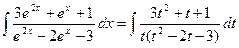
так как 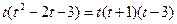 , то разложение простейшей дроби имеет вид
, то разложение простейшей дроби имеет вид
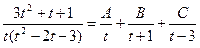
освобождаясь от знаменателей получим
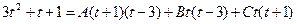
если t=0, то 1=-3А, т.е. А=-1/3, если же t=-t, то 2=4В, т.е. В=1/2, наконец, если t=3, то 31=12С, т.е. С=31/12
Итак,
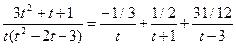
и значит
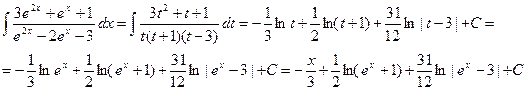
▲
Найти интегралы:
1442. 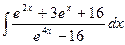
1443.