Статистический анализ случайных погрешностей

При выполнении многократных измерений необходим метод, который позволил бы обрабатывать полученные результаты. Одним из удобных методов является использование распределения. Предельным распределением (при бесконечном количестве измерений) результатов эксперимента является распределение Гаусса. Однако оно не является единственно возможным.

Вопросу обоснования применимости распределения Гаусса в теории ошибок в литературе уделяется много внимания. Но лучше всего, касаясь этого вопроса, пожалуй, сказал тот, кто сказал «экспериментаторы верят в него, полагаясь на доказательства математиков, а математики – полагаясь на экспериментальное обоснование». И, тем не менее, распределение Гаусса можно в какой-то мере обосновать.

Распределение Гаусса отражает следующие предположения, лежащие в основе теории случайных погрешностей и подтверждаемые опытом:

1. Погрешности результатов измерений принимают непрерывный ряд значений.

2. При большом числе измерений:

- одинаково часто встречаются погрешности одного значения, но разных знаков;

- чем больше погрешность измерения, тем реже это измерение встречается.

Отсюда следует, что распределение Гаусса графически изображается в виде кривой, симметричной относительно истинного значения Х измеряемой величины, имеющей колоколообразную форму (Рис. 1).

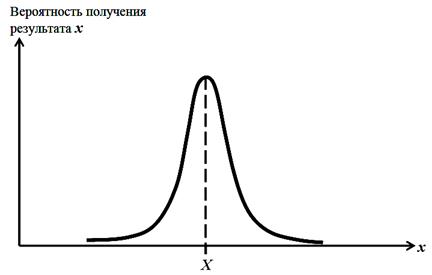
Рис. 2

В теории доказывается, что наилучшей оценкой истинного значения Х измеряемой физической величины является её среднее значение, рассчитываемое на основе прямых измерений по формуле:

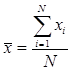. (3.1)

Проявление случайной погрешности при прямых измерениях определяется путём расчёта статистической погрешности:

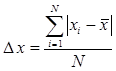. (3.2)

В формулах (3.1) и (3.2): N – количество прямых измерений величины х; х_i – результаты однократных измерений.