Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параболическая корреляция
|
|
Уравнение регрессии в форме параболы имеет вид:
| у=а+bx+сх2 |
При параболической корреляции связь между результативным и факторным признаками может поменять знак на противоположный, из прямой превратиться в обратную, из обратной в прямую[1].
Например, с увеличением дозы удобрений урожайность сначала возрастает, но если превысить оптимальную дозу, то при дальнейшем увеличении дозы удобрений растения угнетаются, и урожайность падает.
Чтобы вычисленные по параболе значения результативного признака были как можно ближе к фактическим значениям yi, будем искать такую параболу второго порядка, соответствующие ординаты которой дают наименьшую сумму квадратов отклонений от фактических (найденных наблюдением) значений yi, т.е. будем искать, при каких a, b, c будет минимальной сумма:
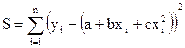
Дифференцируем ее по очереди по a, b и с и приравниваем нулю частные производные. После простых преобразований получим следующую систему нормальных уравнений:
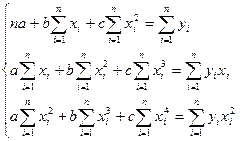
Если расчет производится не по индивидуальным данным, а на основе группировки, то нормальные уравнения имеют вид:
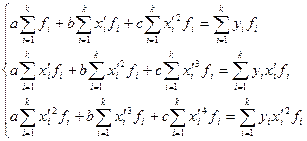
Решая эту систему, получаем значения параметров а, b и с.
Нахождение параболы методом наименьших квадратов называют выравниванием по параболе.
Выравнивание по параболе находит разнообразное применение в экономической науке. Одним из самых важных применений является разыскание экстремумов рассматриваемой функции, если она параболически зависит от аргумента.
Пример. Параболическая корреляционная связь продуктивности коров и себестоимости молока по данным группировки сельхозпредприятий области:
| Группы предприятий по надою, хi, т | Число предприятий, fi | Середина интервала, xi¢, т | Средняя себестоимость молока, yi, у.е. за 1т | Расчетные графы | ||||||||||||
| xi¢ fi | xi¢ 2fi | xi¢ 3fi | xi¢ 4fi | yifi | yixi¢ fi | yixi¢ 2fi | ||||||||||
| до 3, 0 | 2, 80 | 41, 25 | 44, 8 | 125, 4 | 351, 2 | 983, 4 | 660, 0 | 1848, 0 | 5174, 4 | |||||||
| 3, 0-3, 5 | 3, 25 | 36, 67 | 136, 5 | 443, 6 | 1441, 8 | 4685, 8 | 1540, 1 | 5005, 5 | 16267, 7 | |||||||
| 3, 5-4, 0 | 3, 75 | 32, 50 | 116, 2 | 435, 9 | 1634, 8 | 6130, 4 | 1007, 5 | 3778, 1 | 14168, 0 | |||||||
| 4, 0-4, 5 | 4, 25 | 28, 89 | 76, 5 | 325, 1 | 1381, 8 | 5872, 6 | 520, 0 | 2210, 1 | 9392, 9 | |||||||
| 4, 5-5, 0 | 4, 75 | 29, 04 | 61, 8 | 293, 3 | 1393, 2 | 6617, 9 | 377, 5 | 1793, 2 | 8517, 8 | |||||||
| 5, 0-5, 5 | 5, 25 | 29, 17 | 47, 2 | 248, 1 | 1302, 3 | 6837, 2 | 262, 5 | 1378, 3 | 7236, 3 | |||||||
| более 5, 5 | 6, 00 | 31, 07 | 42, 0 | 252, 0 | 1512, 0 | 9072, 0 | 217, 5 | 1304, 9 | 7829, 6 | |||||||
| Итого | 33, 71 | 525, 0 | 2123, 4 | 9017, 1 | 40199, 3 | 4585, 1 | 17318, 1 | 68586, 4 | ||||||||
В этой же таблице приведены расчетные величины для системы нормальных уравнений:
 Þ с=2, 3249; b=-23, 64; а=88, 68
Þ с=2, 3249; b=-23, 64; а=88, 68
Тогда у=88, 68-23, 641х+2, 3249х2
На рисунке нанесены точки наблюдений и построена кривая корреляции (часть параболы):