
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гиперболическая корреляция
|
|
Уравнение регрессии в форме гиперболы имеет вид:
у=а+ 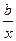
|
х®¥ Þ у®а.
Таким образом, гиперболические зависимости характерны для связей, в которых результативный признак не может варьироваться неограниченно, его вариация имеет односторонний предел.
Например, при освоении нового оборудования его производительность возрастает, но рост замедлится при приближении к конструктивно-технологическому пределу производственной мощности агрегата.
Нормальные уравнения метода наименьших квадратов для гиперболы имеют вид:

Если расчет производится не по индивидуальным данным, а на основе группировки, то нормальные уравнения имеют вид:
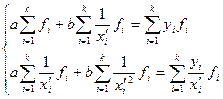
Решая эту систему, получаем значения параметров а, b и с.
В экономических исследованиях часто рассматривается связь между уровнем себестоимости (у) и размером выпуска продукции (х), которая описывается гиперболой.
Пример. Гиперболическая связь себестоимости прироста со скоростью прироста массы скота в совокупности предприятий области, занимавшихся откормом скота:
| Группы предприятий по приросту массы, хi, г на 1 голову | Число предприятий, fi | Середина интервала, xi¢, 100г на 1 голову | Средняя себестоимость прироста, yi, у.е. /ц | Расчетные графы | ||||||
| fi/xi¢ | fi/xi¢ 2 | yifi | yifi/xi¢ | yi расч | yi расч - 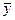
| (yi расч - 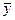 )2fi )2fi
| ||||
| 334-425 | 3, 8 | 5, 79 | 1, 52 | |||||||
| 425-516 | 4, 7 | 7, 87 | 1, 67 | |||||||
| 516-607 | 5, 6 | 5, 00 | 0, 89 | -31 | ||||||
| 607-698 | 6, 5 | 4, 15 | 0, 64 | -77 | ||||||
| 698-789 | 7, 4 | 1, 22 | 0, 16 | -112 | ||||||
| Итого | 24, 03 | 4, 88 |
В этой же таблице приведены расчетные величины для системы нормальных уравнений:
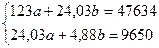 Þ b=1857; а=24, 44
Þ b=1857; а=24, 44
Тогда у=24, 44+ 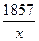
На рисунке нанесены точки наблюдений и построена кривая корреляции (часть гиперболы):
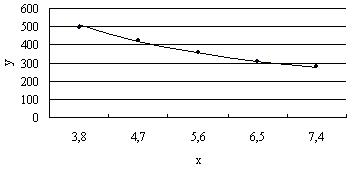
[1] При прямых связях с увеличением признака х увеличивается и признак у, при обратных связях с увеличением признака х признак у уменьшается.