
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общая Электротехника и электроника
|
|
Методические указания
По выполнению расчётно-графической работы № 1
по дисциплине
общая Электротехника и электроника
Направление подготовки: 270100 «Строительство»
Специальности подготовки: 270002 «Промышленное и гражданское
строительство»
270005 «Городское строительство и хозяйство»
170006 «Производство строительных материалов,
изделий и конструкций»
270009 «Теплогазоснабжение и вентиляция»
270012 «Водоснабжение и водоотведение»
Форма обучения – очная, заочная
Тула 2012
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………………................................................................
ПРОГРАММА ИЗУЧЕНИЯ ДИСЦИПЛИНЫ ………………………………..........................
КОНТРОЛЬНЫЕ ЗАДАНИЯ, МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИХ
ВЫПОЛНЕНИЮ, ПРИМЕРЫ РАСЧЁТА …………..................................................................
ЗАДАЧА 1. Расчёт линейной цепи постоянного тока методом двух законов Кирхгофа
и предварительным преобразование треугольника резисторов в эквивалентную звезду..... 7
ЗАДАЧА 2. Расчет линейной цепи постоянного тока методом активного двухполюсника (эквивалентного генератора) ……………….............................................................................................................. 7
ЗАДАЧА 3. Расчет последовательной нелинейной цепи постоянного тока ………............... 7
ЗАДАЧА 4. Расчет параллельной нелинейной цепи постоянного тока ………….................. 7
ЗАДАЧА 5. Расчет неразветвленной неоднородной магнитной цепи с постоянной магнитодвижущей силой …………………………………………...........................................................................................
ЗАДАЧА 6. Расчет последовательной цепи синусоидального тока …………….....................
ЗАДАЧА 7. Расчет параллельной цепи синусоидального тока …………………....................
ЗАДАЧА 8. Расчет смешанной цепи синусоидального тока …………………........................
ЗАДАЧА 9. Расчёт трехфазной четырёхпроводной цепи, соединенной звездой ……...........
ЗАДАЧА 10. Расчет трехфазной цепи, соединенной треугольником ………………..............
ЗАДАЧА 11. Расчет характеристик трехфазного трансформатора …………………...............
ЗАДАЧА 12. Расчет характеристик асинхронного трехфазного двигателя с короткозамкнутым ротором ……………………………………………………….......................................................................
ЗАДАЧА 13 Расчет характеристик асинхронного двигателя с фазным ротором ……...........
ЗАДАЧА 14. Расчет характеристик двигателя постоянного тока параллельного
возбуждения ……………………………………………………………........................................
ВВЕДЕНИЕ
Материал предназначен для студентов очного и заочного обучения всех не электрических специальностей. В его состав входят – общие методические указания к выполнению контрольно-курсовых работ, условия задач с методическими указаниями и примерами расчёта.
Материал включает контрольные работы по следующим разделам курса: электрические и магнитные цепи постоянного тока; однофазные цепи синусоидального тока; трехфазные цепи; трансформаторы; асинхронно трехфазные цепи; двигатели постоянного тока параллельного возбуждения.
Методические указания и контрольные задания выдаются кафедрой каждому студенту на период выполнения контрольно-курсовых работ и подлежат обязательному возврату на кафедру вместе с последнее работой.
Оформление контрольно-курсовых работ осуществляется на листах формата А4 или в ученических тетрадях в клетку, чернилами или пастой. Все чертежи и схемы выполняются с применением чертежных инструментов в соответствии с действующими ГОСТами. Сокращения и исправления в текстах не допускаются. Расчёты производятся с точностью то третьей значащей цифры.
Работа должна содержать титульный лист, на котором указываются: полное наименование учебного заведения, имя, фамилия и отчество студента, номер учебной группы, номера личного и группового вариантов, дата выполнения контрольной работы. Пример оформления титульного листа представлен в приложении А.
Номер личного варианта представляет собой порядковый номер фамилии студента в групповом журнале.
Номер группового варианта указывается преподавателем.
КОНТРОЛЬНЫЕ ЗАДАНИЯ, МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ИХ ВЫПОЛНЕНИЮ, ПРИМЕРЫ РАСЧЁТА
ЗАДАЧА 1. Расчёт линейной цепи постоянного тока методом двух законов Кирхгофа и предварительным преобразование треугольника резисторов в эквивалентную звезду.
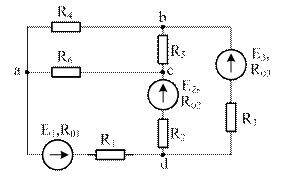
В цепи, схема которой приведена на рисунке 1, необходимо:
1. Преобразовать треугольник резисторов R4, R5, R6 в эквивалентную звезду и затем методом двух законов Кирхгофа определить токи в ветвях преобразованной цепи
2. Определить напряжения Uab, Ubc, Uca, и токи I4, I5, I6 исходной цепи.
3. Составить уравнение баланса мощностей для исходной цепи с целью проверки правильности расчёта токов (расхождение баланса мощностей не должно превышать 3 %). Номер схемы и чистовые данные к расчёту определяются по таблице 1 и 2.

| 
|
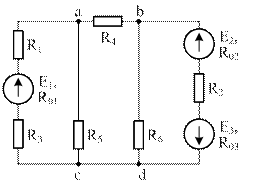
| Схема 1 | Схема 2 |
| 
|
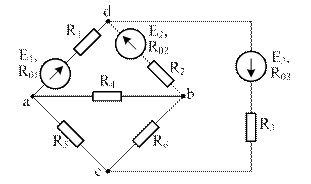
| Схема 3 | Схема 4 |
| 
|
| Схема 5 | Схема 6 |
Рисунок 1
Таблица 1 – Личные варианты
| Номер личного варианта | Номер схемы | Параметры источника ЭДС | |||||
| E1, B | R01, Oм | Е2, В | R02, Ом | Е3, В | R03, Ом | ||
Таблица 2 – Групповые варианты
| Номер группового варианта | Сопротивления резисторов, Ом | |||||
| R1 | R2 | R3 | R4 | R5 | R6 | |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЁТА
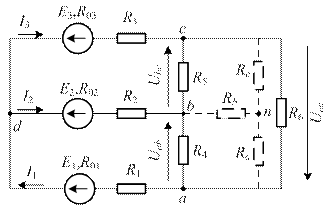
Решение данной задачи рассматривается на примере цепи, представленной на рисунке 2, в которой  ,
,  ,
, 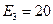 В;
В;  ,
,  ,
,  ,
,  ,
,  ,
, 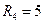 ,
, 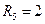 ,
,  Ом.
Ом.
| 
|
| Рисунок 2 | Рисунок 3 |
Замена треугольника резисторов 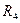 ,
,  ,
, 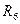 эквивалентной звездой резисторов
эквивалентной звездой резисторов 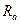 ,
, 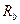 ,
, 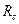 осуществляется следующим образом. К узловым точкам a, b, c или к проводам, связанным с этими точками, подключается эквивалентная звезда резисторов (на рисунке 2 она показана штриховыми линиями). Определяются сопротивления резисторов эквивалентной звезды:
осуществляется следующим образом. К узловым точкам a, b, c или к проводам, связанным с этими точками, подключается эквивалентная звезда резисторов (на рисунке 2 она показана штриховыми линиями). Определяются сопротивления резисторов эквивалентной звезды:
 ;
;  ;
; 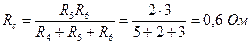
Вычерчивается схема цепи (рисунок 3), получившаяся после замены треугольника резисторов эквивалентной звездой.
Токи  ,
,  ,
, 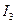 определяются на основе преобразованной цепи в следующем порядке. На схему наносятся произвольные направления исходных токов (здесь все три тока направлены к узлу d). Задается направление обхода по контурам (оно здесь принято совпадающим с направлением движения часовой стрелки). Составляется ситстема уравнений по законам Кирхгофа:
определяются на основе преобразованной цепи в следующем порядке. На схему наносятся произвольные направления исходных токов (здесь все три тока направлены к узлу d). Задается направление обхода по контурам (оно здесь принято совпадающим с направлением движения часовой стрелки). Составляется ситстема уравнений по законам Кирхгофа:


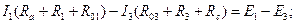
Подставив в данную систему уравнений числовые значения и решив ее, получаем
 ;
;  ;
;  .
.
Знак минус у значений токов  и
и 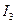 означает, что их истинные направления противоположны направлениям, принятым на рисунке 3, т.е. они направлены от узла d. На схеме (рисунок 2) нанесены истинные направления этих токов.
означает, что их истинные направления противоположны направлениям, принятым на рисунке 3, т.е. они направлены от узла d. На схеме (рисунок 2) нанесены истинные направления этих токов.
Напряжения 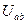 ,
,  ,
,  определяются из решений уравнений, составленных по второму закону Кирхгофа для контуров abna, bcnb, canc:
определяются из решений уравнений, составленных по второму закону Кирхгофа для контуров abna, bcnb, canc:  ;
;  ;
;  . Подставив в данные уравнения числовые значения и решив их, получаем:
. Подставив в данные уравнения числовые значения и решив их, получаем:  ,
,  ,
,  .
.
Токи  ,
, 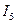 ,
,  в исходной цепи (рисунок 2) определяются по закону Ома:
в исходной цепи (рисунок 2) определяются по закону Ома: 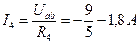 ;
;  ;
; 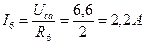 . Знак минус у значения тока
. Знак минус у значения тока  означает, что этот ток направлен от узла b к узлу a.
означает, что этот ток направлен от узла b к узлу a.
Уравнение баланса мощностей для исходной цепи (рисунок 2) имеет следующий вид: 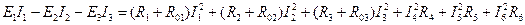 . В данной цепи мощность первого источника положительная, т.к. в нем направления ЭДС и тока совпадают (режим генератора), мощности второго и третьего источников отрицательные, так как в них направления ЭДС и токов противоположны (режим приёмника). Подставив в данное уравнение числовые значения и решив его, получаем: 88 Вт = 88 Вт. Баланс сошёлся, значит токи найдены правильно.
. В данной цепи мощность первого источника положительная, т.к. в нем направления ЭДС и тока совпадают (режим генератора), мощности второго и третьего источников отрицательные, так как в них направления ЭДС и токов противоположны (режим приёмника). Подставив в данное уравнение числовые значения и решив его, получаем: 88 Вт = 88 Вт. Баланс сошёлся, значит токи найдены правильно.
ЗАДАЧА 2. Расчёт линейной цепи постоянного тока методом активного двухполюсника (эквивалентного генератора).
Методом активного двухполюсника определить ток, протекающий через один из резисторов цепи, схема которой представлена на рисунке 4. Номер схемы и числовые данные к расчёту приведены в таблице 4. Наименование резистора, ток которого подлежит определению, приведено в таблице 4.

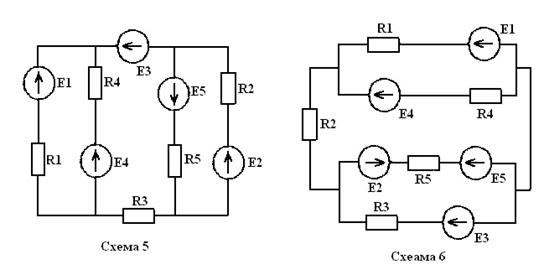
Рисунок 4
Таблица 3 – Личные варианты
| Номер личного варианта | Номер схемы | Значения ЭДС, В | Сопротивления, Ом | ||||||||
| E1 | E2 | E3 | E4 | E5 | R1 | R2 | R3 | R4 | R5 | ||
Таблица 4 – Групповые варианты
| Номер группового варианта | |||||
| Резистор, в котором требуется определить ток | R1 | R2 | R3 | R4 | R5 |
МЕТОДИЧЕСКИЙ УКАЗАНИЯ И ПРИМЕР РАСЧЁТА
Решение данной задачи рассматривается на примере цепи, представленной на рисунке 5, в которой 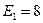 ,
, 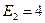 ,
,  ,
,  ;
;  ,
, 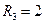 ,
,  ,
,  . Требуется определить ток в резисторе
. Требуется определить ток в резисторе 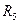 .
.
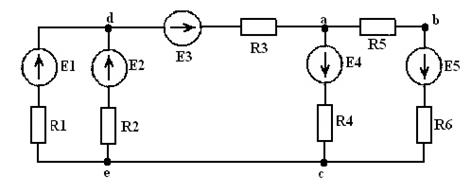
Рисунок 5
Решение данной задачи осуществляется в 4 этапа:
1. Заданная цепь разделяется на активный двухполюсник и его нагрузку. В данной цепи нагрузкой является резистор 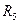 , а вся остальная часть цепи – активным двухполюсником;
, а вся остальная часть цепи – активным двухполюсником;
2. Определяется напряжение холостого хода 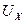 на зажимах активного двухполюсника;
на зажимах активного двухполюсника;
3. Определяется входное сопротивление 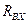 пассивной части активного двухполюсника;
пассивной части активного двухполюсника;
4. Определяется искомый ток 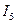 , протекающий через резистор
, протекающий через резистор 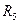 .
.
Напряжение 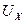 определяется в следующем порядке. Вычерчивается схема активного двухполюсника при холостом ходе (рисунок 6). Определяются тока холостого хода
определяется в следующем порядке. Вычерчивается схема активного двухполюсника при холостом ходе (рисунок 6). Определяются тока холостого хода 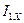 ,
,  ,
, 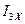 активного двухполюсника методом двух законов Кирхгофа. Для этого составляется и решается система трех уравнений и неизвестными точками
активного двухполюсника методом двух законов Кирхгофа. Для этого составляется и решается система трех уравнений и неизвестными точками 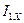 ,
,  ,
, 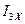 :
:

Рисунок 6
 ;
;
 ;
;
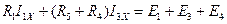 .
.
Подставив в данную систему уравнений числовые значения и решив ее, получаем:  ;
;  ;
; 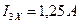 . Определяется напряжение
. Определяется напряжение 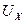 из решения уравнения, которое составляется по второму закону Кирхгофа для контура abca:
из решения уравнения, которое составляется по второму закону Кирхгофа для контура abca: 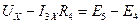 ;
; 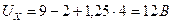 .
.
Сопротивление 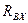 определяется в следующем порядке. Вычерчивается схема пассивной части активного двухполюсника (рисунок 7), которая получается из схемы активного двухполюсника путем исключения из нее источников ЭДС. Сопротивление
определяется в следующем порядке. Вычерчивается схема пассивной части активного двухполюсника (рисунок 7), которая получается из схемы активного двухполюсника путем исключения из нее источников ЭДС. Сопротивление 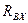 представляет собой эквивалентное сопротивление цепи, схема которой приведена на рисунке 7. Оно определяется в 2 этапа:
представляет собой эквивалентное сопротивление цепи, схема которой приведена на рисунке 7. Оно определяется в 2 этапа:
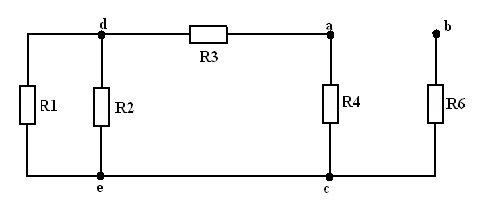
Рисунок 7
1. Определяется эквивалентное сопротивление  части цепи, расположенной слева от узлов a и c:
части цепи, расположенной слева от узлов a и c:
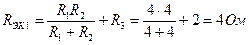
2. Определяется сопротивление 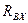 :
:

Искомый ток 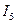 определяется по формуле:
определяется по формуле:

ЗАДАЧА 3. Расчёт последовательной нелинейной цепи постоянного тока.
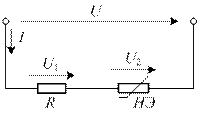
Рисунок 8
В цепи, общая схема которой приведена рисунке 8, по заданному напряжению 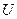 на зажимах цепи определить ток
на зажимах цепи определить ток 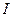 и напряжение
и напряжение 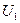 и
и  на элементах. Задачу решить методами сложения и пересечения характеристик. Схема конкретной цепи, подлежащей расчёту, получается из общей схемы путём замены в ней резистора R и нелинейного элемента НЭ конкретными элементами согласно данным таблицы 5. Числовые значения сопротивлений резисторов и вольт-амперных характеристик (ВАХ) нелинейных элементов приведены в таблице 6 и 7.
на элементах. Задачу решить методами сложения и пересечения характеристик. Схема конкретной цепи, подлежащей расчёту, получается из общей схемы путём замены в ней резистора R и нелинейного элемента НЭ конкретными элементами согласно данным таблицы 5. Числовые значения сопротивлений резисторов и вольт-амперных характеристик (ВАХ) нелинейных элементов приведены в таблице 6 и 7.
Таблица 5 – Числовые значения напряжения и элементы цепи (R и НЭ)
| Номер личного варианта | Последовательная цепь | Параллельная цепь | ||||
| U, B | R | НЭ | I, A | НЭ* | НЭ** | |
| R1 | НЭ2 | НЭ10 | НЭ9 | |||
| R1 | НЭ3 | НЭ10 | НЭ8 | |||
| R1 | НЭ4 | НЭ10 | НЭ7 | |||
| R1 | НЭ5 | НЭ10 | НЭ6 | |||
| R1 | НЭ6 | НЭ10 | НЭ5 | |||
| R2 | НЭ1 | НЭ10 | НЭ4 | |||
| R2 | НЭ2 | НЭ9 | НЭ8 | |||
| R2 | НЭ3 | НЭ9 | НЭ7 | |||
| R2 | НЭ4 | НЭ9 | НЭ6 | |||
| R2 | НЭ5 | НЭ9 | НЭ5 | |||
| R2 | НЭ6 | НЭ9 | НЭ4 | |||
| R3 | НЭ1 | НЭ8 | НЭ7 | |||
| R3 | НЭ2 | НЭ8 | НЭ6 | |||
| R3 | НЭ3 | НЭ8 | НЭ5 | |||
| R3 | НЭ4 | НЭ8 | НЭ4 | |||
| R3 | НЭ5 | НЭ7 | НЭ6 | |||
| R4 | НЭ1 | НЭ7 | НЭ5 | |||
| R4 | НЭ2 | НЭ7 | НЭ4 | |||
| R4 | НЭ3 | НЭ6 | НЭ5 | |||
| R4 | НЭ4 | НЭ6 | НЭ4 | |||
| R5 | НЭ1 | НЭ5 | НЭ4 | |||
| R5 | НЭ2 | НЭ4 | НЭ3 | |||
| R5 | НЭ3 | НЭ5 | НЭ3 | |||
| R5 | НЭ1 | НЭ6 | НЭ3 | |||
| R5 | НЭ2 | НЭ7 | НЭ3 |
Таблица 6 – Числовые значения сопротивлений
| Сопротивления резисторов, Ом | |||||
| R1 | R2 | R3 | R4 | R5 | R6 |
| 0, 35 | 0, 5 | 0, 6 | 0, 75 | 0, 9 | 1, 0 |
Таблица 7 – Числовые значения нелинейных элементов
| Вольтамперные характеристики нелинейных элементов | ||||||||||
| U, В | Токи, А | |||||||||
| НЭ1 | НЭ2 | НЭ3 | НЭ4 | НЭ5 | НЭ6 | НЭ7 | НЭ8 | НЭ9 | НЭ10 | |
| 0, 1 | 0, 2 | 0, 2 | 2, 5 | 4, 0 | 6, 7 | 0, 4 | 3, 3 | 2, 2 | 1, 4 | |
| 0, 2 | 0, 7 | 0, 5 | 4, 2 | 5, 9 | 7, 8 | 1, 5 | 5, 6 | 3, 8 | 2, 1 | |
| 4, 5 | 1, 5 | 0, 8 | 4, 3 | 6, 1 | 8, 0 | 9, 1 | 6, 2 | 4, 4 | 2, 6 | |
| 16, 0 | 2, 7 | 1, 3 | 4, 3 | 6, 2 | 8, 1 | 9, 4 | 6, 8 | 4, 9 | 2, 9 | |
| - | 4, 3 | 1, 8 | 4, 4 | 6, 2 | 8, 1 | 9, 5 | 7, 2 | 5, 2 | 3, 2 | |
| - | 16, 0 | 2, 7 | 4, 4 | 6, 3 | 8, 2 | 9, 5 | 7, 4 | 5, 4 | 3, 4 | |
| - | - | 4, 5 | 4, 5 | 6, 4 | 8, 2 | 9, 6 | 7, 6 | 5, 6 | 3, 5 |
Продолжение таблицы 7
| Вольтамперные характеристики нелинейных элементов | ||||||||||
| U, В | Токи, А | |||||||||
| НЭ1 | НЭ2 | НЭ3 | НЭ4 | НЭ5 | НЭ6 | НЭ7 | НЭ8 | НЭ9 | НЭ10 | |
| - | - | 16, 0 | 4, 8 | 6, 4 | 8, 3 | 9, 6 | 7, 7 | 5, 7 | 3, 6 | |
| - | - | - | 10, 0 | 6, 7 | 8, 4 | 9, 7 | 7, 7 | 5, 7 | 3, 7 | |
| - | - | - | 16, 0 | 10, 0 | 8, 4 | 9, 7 | 7, 8 | 5, 7 | 3, 7 | |
| - | - | - | 16, 0 | 9, 3 | 9, 8 | 7, 8 | 5, 8 | 3, 8 | ||
| - | - | - | - | - | 16, 0 | 9, 8 | 7, 8 | 5, 8 | 3, 8 | |
| - | - | - | - | - | - | 9, 8 | 7, 9 | 5, 9 | 3, 8 | |
| - | - | - | - | - | - | 9, 9 | 7, 9 | 5, 9 | 3, 9 | |
| - | - | - | - | - | - | 9, 9 | 7, 9 | 5, 9 | 3, 9 | |
| - | - | - | - | - | - | 10, 0 | 8, 0 | 6, 0 | 4, 0 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЁТА
Решение данной задачи рассматривается на примере цепи, приведенной на рисунке 9, элементами которой являются резистор 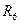 и нелинейный элемент НЭ 3. Согласно таблице 6 сопротивление
и нелинейный элемент НЭ 3. Согласно таблице 6 сопротивление  . Напряжение
. Напряжение  .
.
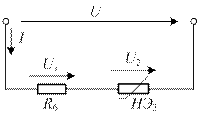
Рисунок 9
Сущность метода сложения характеристик состоит в следующем. В осях координат 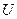 ,
, 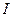 строятся ВАХ элементов цепи
строятся ВАХ элементов цепи 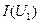 ,
, 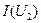 и ВАХ всей цепи
и ВАХ всей цепи  (рисунок 10).
(рисунок 10).
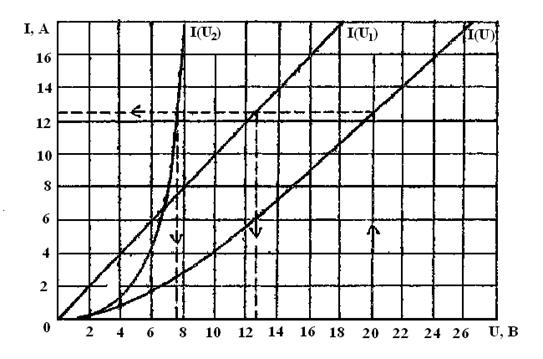
Рисунок 10
Затем используя эти характеристики, графическим путём по заданной величине определяют искомые величины.
ВАХ резистора 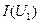 представляет собой прямую линию, проходящую через начало координат. Вторая, вспомогательная, точка (точка B) этой прямой определяется с помощью закона Ома. Для этого в пределах оси
представляет собой прямую линию, проходящую через начало координат. Вторая, вспомогательная, точка (точка B) этой прямой определяется с помощью закона Ома. Для этого в пределах оси 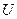 задается абсцисса
задается абсцисса  этой точки, а затем определяется ордината
этой точки, а затем определяется ордината 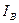 этой точки по закону Ома:
этой точки по закону Ома:  . ВАХ нелинейного элемента
. ВАХ нелинейного элемента 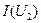 строится по значениям, приведенным в таблице 7.
строится по значениям, приведенным в таблице 7.
Характеристики  строится на основе второго закона Кирхгофа:
строится на основе второго закона Кирхгофа:  . Это уравнение в данном случае следует понимать так: для каждого фиксированного значения тока напряжение на зажимах цепи равно сумме падений напряжений на элементах цепи. А это значит, что для построения кривой
. Это уравнение в данном случае следует понимать так: для каждого фиксированного значения тока напряжение на зажимах цепи равно сумме падений напряжений на элементах цепи. А это значит, что для построения кривой  следует задать ряд значений тока (8-10 значений в пределах оси ординат) и для каждого тока найти значение напряжения путём сложения абсцисс кривых
следует задать ряд значений тока (8-10 значений в пределах оси ординат) и для каждого тока найти значение напряжения путём сложения абсцисс кривых 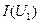 и
и 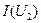 . При этом на плоскости координат будет получен ряд точек, при соединении которых получится искомая кривая
. При этом на плоскости координат будет получен ряд точек, при соединении которых получится искомая кривая  .
.
В рассматриваемом примере  . Согласно кривой
. Согласно кривой  данному значению напряжения соответствует ток, равный 12, 4 А. Согласно кривым
данному значению напряжения соответствует ток, равный 12, 4 А. Согласно кривым 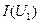 и
и 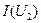 данному значению тока соответствуют следующие напряжения на элементах цепи:
данному значению тока соответствуют следующие напряжения на элементах цепи: 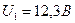 ;
;  .
.
Расчёт данной цепи методом пересечения характеристик осуществляется следующим образом. Заданная цепь представляется состоящей из двух частей: в первую часть входят источник напряжения 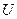 и резистор
и резистор 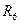 , во вторую – нелинейный элемент НЭЗ. Первая часть заменяется эквивалентным генератором с параметрами:
, во вторую – нелинейный элемент НЭЗ. Первая часть заменяется эквивалентным генератором с параметрами:
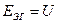 ;
;  ;
; 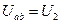 ,
,
где 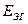 ,
, 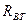 ,
, 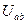 – ЭДС, внутреннее сопротивление, выходное напряжение эквивалентного
– ЭДС, внутреннее сопротивление, выходное напряжение эквивалентного
генератора.
Нелинейный элемент рассматривается как нагрузка эквивалентного генератора (рисунок 11).
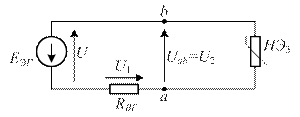
Рисунок 11
Уравнение внешней характеристики данного эквивалентного генератора, полученное на основании второго закона Кирхгофа, имеет следующий вид:
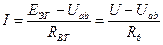 .
.
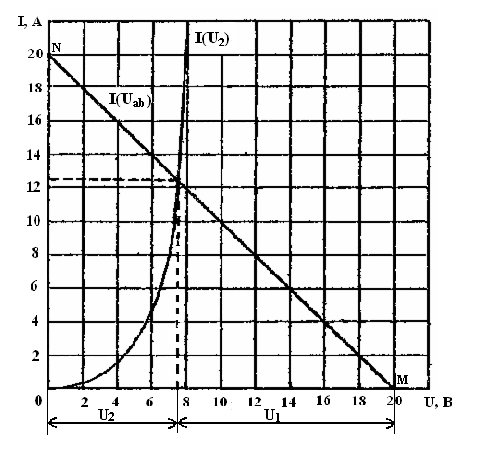
Рисунок 12
Согласно этому уравнению в осях 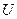 ,
, 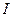 (рисунок 12) строится график этой характеристики
(рисунок 12) строится график этой характеристики  . Он представляет собой прямую линию, пересекающую оси координат в точках M и N. Координаты точки M определяются из опыта холостого хода, а точки N из опыта короткого замыкания эквивалентного генератора. При холостом ходе
. Он представляет собой прямую линию, пересекающую оси координат в точках M и N. Координаты точки M определяются из опыта холостого хода, а точки N из опыта короткого замыкания эквивалентного генератора. При холостом ходе 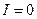 , а
, а 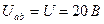 . Из этого следует, что абсцисса точки М равна 20, а ордината – нулю. При опыте короткого замыкания
. Из этого следует, что абсцисса точки М равна 20, а ордината – нулю. При опыте короткого замыкания  , а
, а 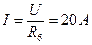 . Из этого следует, что абсцисса точки N равна нулю, а ордината – 20.
. Из этого следует, что абсцисса точки N равна нулю, а ордината – 20.
В этих же осях координат строится ВАХ нелинейного элемента по значениям, приведенным в таблице 7.
Искомые ток и напряжения 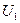 и
и  определяются точкой пересечения прямой
определяются точкой пересечения прямой  и кривой
и кривой 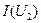 (точкой A). Ордината этой точки равна искомому току, а ее абсцисса разделяет отрезок OM на две части. Одна часть численно равна
(точкой A). Ордината этой точки равна искомому току, а ее абсцисса разделяет отрезок OM на две части. Одна часть численно равна 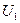 , а другая
, а другая  (рисунок 12).
(рисунок 12).
ЗАДАЧА 4. Расчёт параллельной нелинейной цепи постоянного тока.
В цепи, общая схема которой приведена на рисунке 13 по заданному значению тока 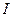 определить напряжение и токи
определить напряжение и токи  ,
,  конкретной цепи. Схема конкретной цепи, подлежащая расчету, получается из общей схемы (рисунок 13) путем замены в ней нелинейных элементов НЭ* и НЭ** конкретными нелинейными элементами согласно данным таблицы 5. Числовые значения ВАХ нелинейных элементов приведены в таблице 7.
конкретной цепи. Схема конкретной цепи, подлежащая расчету, получается из общей схемы (рисунок 13) путем замены в ней нелинейных элементов НЭ* и НЭ** конкретными нелинейными элементами согласно данным таблицы 5. Числовые значения ВАХ нелинейных элементов приведены в таблице 7.

Рисунок 13
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЁТА
Решение данной задачи рассматривается на примере цепи с нелинейными элементами НЭ3 и НЭ8, схема которой приведена на рисунке 14. Ток  . Данная задача решается следующим образом.
. Данная задача решается следующим образом.

Рисунок 14
В осях координат 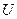 ,
, 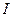 строится ВАХ нелинейных элементов
строится ВАХ нелинейных элементов  и
и  , согласно данным таблицы 7 и ВАХ всей цепи
, согласно данным таблицы 7 и ВАХ всей цепи  (рисунок 15).
(рисунок 15).
Характеристика  строится на основе первого закона Кирхгофа:
строится на основе первого закона Кирхгофа:  . В данном случае это уравнение следует понимать так: для каждого фиксированного значения напряжения
. В данном случае это уравнение следует понимать так: для каждого фиксированного значения напряжения 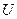 значение общего тока
значение общего тока 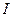 равно сумме токов в ветвях. А это значит, что для построения кривой
равно сумме токов в ветвях. А это значит, что для построения кривой  следует задать ряд значений напряжения
следует задать ряд значений напряжения 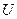 (8-10 значений в пределах оси абсцисс) и для каждого значения напряжения найти значение общего тока
(8-10 значений в пределах оси абсцисс) и для каждого значения напряжения найти значение общего тока 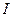 путем сложения ординат характеристик
путем сложения ординат характеристик  и
и  .
.
При этом на плоскости координат будет получено множество точек, при соединении которых получиться кривая  .
.
В рассматриваемом примере 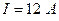 . Согласно кривой
. Согласно кривой  данному значению тока соответствует напряжения
данному значению тока соответствует напряжения  . Согласно кривым
. Согласно кривым  и
и  данному значению напряжения соответствуют следующие значения токов в ветвях цепи:
данному значению напряжения соответствуют следующие значения токов в ветвях цепи:  ;
;  .
.

Рисунок 15
Приложение A
Форма титульного листа
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Тульский государственный университет»
Институт высокоточных систем им. В.П.Грязева
Кафедра электротехники и электрооборудования
|