Биологическая активность ПЛР-спектров препаратов ДНК

Препараты ДНК, использованные нами для " записи" их ПЛР-спектров, через поляризационно-радиоволновую компоненту (ДНК-радиоволны) оказывают специфическое действие на биосистемы, в качестве которых мы использовали клубни картофеля, вызывая их аномально быстрое прорастание (до 1см/сутки). Также был трижды поставлен эксперимент (май 1999г.) по воздействию ДНК-радиоволн на пораженные гама-излучением семена растения Arabidopsis thaliana (L.) Heynh, собранные в зоне Чернобыльской АЭС в 1986-1987 годах[2].

В типичном опыте из 3-х вариантов воздействия на семена (1час 30мин, 1час 40мин и 2часа; мощность дозы 25 мР/час по гамма излучению) «ДНК-радиоволн» в 2-х последних наблюдается увеличение всхожести семян по сравнению с двумя контролями (Р< 0.001). То есть из 300 и 200 посеянных семян в контроле проросли – 2 и 4, а в опыте 16 и 24. Однако, при мощностях дозы выше 170 мР/час эффекта «оживления» семян не наблюдалось. Это говорит о том, что радиоволновое излучение ДНК, полученное данным способом, обладает способностью восстанавливать генетический аппарат и в целом жизнедеятельность семян A. Thaliana, но в ограниченных интервалах мощности дозы гамма-излучения. Существенно и то, что семена длительное время хранились (с 1987г. по 1999г.), что привело к их значительному старению, накладывающему дополнительный деструктивный фактор. Тем не менее, «оживляющий» эффект наблюдается, и это говорит, что ДНК-радиоволновое излучение может нести в себе репаративную генетическую (метаболическую) информацию, что подтверждает наши ранние работы по волновым биознаковым репарирующим воздействиям на гамма-облученные семена пшеницы и ячменя [17, 18]. Возможно, перенос и восприятие такой волновой информации семенами–акцепторами осуществляется по механизму квантовой нелокальности (телепортации), как мы предполагали ранее [5, 19], но в модификации (пермиссивная модель), предложенной в данном исследовании.

Предваряя теоретико-физический анализ предложенной модели телепортации (см. ниже), выскажем несколько суждений относительно значимости этой проблемы для генетики и биологии в целом. В работах [5, 19] вопрос о квантовой нелокальности генома уже обсуждался. В настоящем исследовании эти идеи формализованы и поэтому более обоснованы. Биологические эксперименты, приведенные выше, можно предположительно толковать как демонстрацию переноса генетической информации от препаратов ДНК на биосистемы-реципиенты по механизму квантовой телепортации в пермиссивном варианте. Представляется, что квантовая нелокальность генетической (хромосомной) информации, как проявление ее тотальной распределенности (континуальности) в пространстве многоклеточных биосистем, является частным случаем. В действительности, в биосистемах, по крайней мере, шесть уровней нелокальности.

1-й уровень – организменный. Нелокальность здесь выражается в способности к регенерации, например у червей планарий. После разрезания таких червей любая часть их тела дает при регенерации целый организм. Иными словами, в этом случае отсутствует привязка общего пула генетической информации к какой-то части биосистемы. То же относится к вегетативному размножению растений.

2-й уровень – клеточный. Из каждой клетки, а не только из зиготы, можно вырастить целый организм. Для животных биосистем это затруднено, но возможно. Каждая клетка – потенциальный континуум организма.

3-й уровень – клеточно-ядерный. Энуклеация ядер из соматических и половых клеток с последующим введением в них других ядер не препятствует развитию нормального организма. Клонирование такого рода уже осуществляют на высших биосистемах, например, на овцах. Каждое клеточное ядро – также потенциальный континуум биосистемы. Локализации генетических потенций на каких-то отдельных клетках нет.

4-й уровень – молекулярный: рибосома " читает" информационную РНК не только по отдельным кодонам, но и всю ее целиком с учетом контекста, то есть нелокально, континуально.

5-й уровень – хромосомно-голографический. Геном обладает голографической памятью [26], а это типично распределенная (нелокальная) ассоциативная память. На этом и последующих уровнях нелокальность приобретает новое качество, дуалистический вещественно-волновой характер, поскольку голограммы как вещество " прочитываются" электромагнитными и/или акустическими полями, выносящими гено-волновую информацию за пределы вещества хромосом. На сцену выходит физическое поле или поля, как калибровочная, размечающая будущее пространство организма. Сюда же относится, видимо, голографическая память коры головного мозга, задающая ментальные, смысловые и образные пространства, калибрующие потенциальные действия высших биосистем. В этом реализуются социо-генетические процессы.

6-й уровень – квантовая нелокальность генома. До 6-го уровня нелокальность генетической информации реализуется в пространстве организма. 6-й уровень имеет особый характер и новое качество. Оно проявляется в рамках одной из форм квантовой нелокальности, а именно пермиссивной, постулируемой в данной работе. В этом случае нелокальность реализуется как по пространству биосистемы, так и по ее собственному, «сжимаемому» до нуля, времени. Мгновенно распространяемые такими способами гено-волновые программы, изоморфные вещественным, работают в организме " здесь и там одновременно", поэтому утрачивает смысл семантическая конструкция " сначала и потом". И это стратегический фактор, необычайно важное для многоклеточных биосистем эволюционное достижение. Миллиарды клеток организма должны " знать" друг о друге если не все, то очень многое, причем мгновенно. Без явления «волновой информационной мгновенности» гигантский многоклеточный континуум высших биосистем не способен целостно координировать метаболизм, свои физиологические и другие функции. Межклеточная диффузия сигнальных веществ и нервные процессы слишком инертны для этого. Даже если допустить, что в межклеточной передаче участвуют знаковые электромагнитные поля со световыми скоростями, что достаточно обосновано, то и этого недостаточно. Необходим механизм именно квантовой нелокальности, и он применим к генетическому аппарату, который может выступать как мгновенно распределенный квантовый (волновой) объект, изоморфный вещественным хромосомам [17, 18]. Используя нелокальность, генетический аппарат высших биосистем создает удивительное явление, когда в определенные моменты в «схлопнутом» пространстве-времени биосистемы " здесь и там", " сначала и потом" работают как неразрывность, обеспечивающая организмам суперкогерентность, информационную сверхизбыточность, сверхинформированность, связность и, как итог, целостность (выживаемость). Проявлением этого, например, служит способность к регенерации органов и тканей у низших организмов (гидры, черви, амфибии, ящерицы, ракообразные), способность, которая в значительной степени утрачена человеком. Но ее можно активировать, учитывая развиваемые нами принципы волновой самоорганизации биосистем. Иллюстрацией этого служит первое в мире успешное приживление имплантированных слепому человеку донорских тканей с восстановлением зрения [25]. В основу идеологии такой хирургической операции и регенеративных процессов были положены исследования [17, 18, 26].

Вместе с тем, теоретико-экспериментальные исследования здесь все еще носят начальный характер и нуждаются в физико-математическом осмыслении и развитии. Поэтому в последующей части данной работы мы приводим формализованную модель фотонно-радиоволновых процессов, порождаемых при взаимодействии лазерного пучка с веществом, процессов, которые в предположительном плане можно рассматривать как основу ПЛР-спектроскопии и как простейшую модель волновых информационных событий в хромосомах.

Теоретическая часть

Локализация света в упругом канале рассеяния. Возможность записи и считывания информации, локализованной в пространственно коррелированных неоднородных системах

В экспериментальной части данной работы мы привели результаты, свидетельствущие:

· о возможности считывания спектра собственных возбуждений некоторых кристаллов и биологических структур,

· о возможности долговременного хранения этой информации,

· о возможности последующего считывания и передачи этой информации.

Эксперименты проводили в радиодиапазоне при помощи устройства (ПЛР-спектрометр), описанного выше.

Здесь мы предлагаем одну из возможных теоретических интерпретаций этих экспериментов. В основе наших построений лежат идеи теории локализации света в дисперсных пространственно скоррелированных системах.

Явление локализации света получило широкую известность с 1985 года после работы [1]. Сейчас это одна из наиболее динамично развивающихся областей физики, тесно переплетающаяся с такими «модными» проблемами как, например, квантовая телепортация, новые методы записи и считывания информации и т.д. [6, 12, 13].

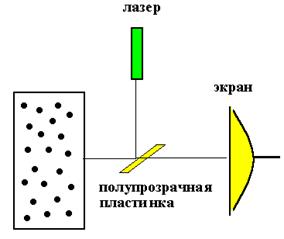Рис. 5. Схема эксперимента по наблюдению слабой локализации света.

В работе [1] исследовали отражение света от прозрачной кюветы, заполненной мельчайшими частицами латекса, взвешенными в воде, в условиях, когда длина волны падающего фотона 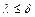( 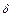- среднее расстояние между частицами). На фоне френелевского отражения, строго в направлении назад наблюдался очень узкий пик интенсивности рассеянного света (Рис.5). Сигнал превышал фоновое значение в 2 раза. Для объяснения эффекта достаточно рассмотреть рассеяние на паре частиц, оказавшихся на пути фотона. Элемент траектории фотона, отразившегося в направлении строго назад, есть расположенная между парой частиц бесконечно узкая петля. Предположим, что эту петлю фотон может пройти двумя способами - по ходу вращения часовой стрелки и наоборот. Эти два способа изображены на Рис. 6 а). Они неразличимы.

Рис. 6. а) два способа прохождения фотоном петли на его траектории в условиях слабой локализации. б) разворот фотона между двумя частицами.

В таких случаях квантовая механика предписывает вычислять вероятность Р разворота фотона следующим образом. Каждому из процессов сопоставляется амплитуда вероятности а и вероятность разворота 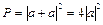(мы учли, что обе амплитуды под знаком модуля имеют одинаковые фазы - в этом особенность движения по петле [14]). Если бы у нас была гипотетическая возможность различить эти способы, вероятность разворота считалась бы совершенно иначе и была бы в два раза меньше: 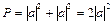. Такова формальная причина пика в направлении назад. Однако, появление пика в направлении назад вовсе не сопровождается соответствующим уменьшением рассеяния света в каком-либо ином направлении [11]. Как же быть в таком случае с законом сохранения энергии и откуда взялись те добавочные фотоны, которые образовали пик? Второй вопрос - почему этот пик не наблюдается при отражении света от сплошного полупространства? И третий вопрос. С чего мы взяли, что существуют два способа движения фотона между парой частиц? Если траектория фотона между частицами одномерная прямая линия, то о каких двух различных способах ее обхода может быть речь? Разворот фотона между двумя рассеивателями - однозначным образом определенная процедура, изображенная на Рис. 6 b).

Итак, нам очень бы хотелось, чтобы было два способа прохождения фотоном бесконечно узкой петли между двумя частицами. Этого можно достичь, если предположить, что топологическая размерность траектории фотона в условиях слабой локализации d< 1. Только в этом случае мы можем разместить внутри одной одномерной линии рисунка 6 b) две разных “линии” - топологический объект, похожий на петлю, т.е. характеризующийся двумя способами его обхода.

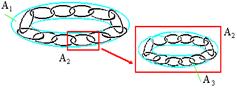Рис.7. Ожерелье Антуана

Существует изящная математическая конструкция, которая, с одной стороны, очень похожа на то, что в физике называется линией или траекторией, а с другой стороны, ее топологическая размерность d действительно меньше единицы. Более того, d=0. Речь идет о т.н. цепочечном множестве Антуана [15]. Этот объект как нельзя лучше приспособлен и для описания процесса непрерывной генерации разномасштабных петель на траектории фотона.

Нульмерное множество Антуана (ожерелье Антуана) устроено следующим образом. На первом этапе рассматривается затравочная “толстая” замкнутая петля А₁. На втором - А₁ заменяется цепочкой менее “толстых” звеньев А₂, находящейся внутри А₁. Затем каждое звено А₂ заменяется цепочкой еще более мелких звеньев А₃ Ì А₂ и т.д. Продолжая этот процесс, получим последовательность А₁ É А₂ É А₃... (см. Рис. 7). Пересечение этих множеств представляет собой нульмерное антуановское множество А^*. Описанная конструкция - простейший вариант антуановского множества.

Несмотря на то, что антуановская цепочка нульмерна, она не утрачивает некоторых свойств обычной одномерной линии. Так, если с обычного нульмерного множества А₀, например, с конечного множества точек легко можно снять “продетое” через него кольцо, нигде не пересекая А₀, то проделать то же самое с нульмерным множеством А^* не удается.

Предположим, что траектория фотона в условиях сильной и слабой локализации является антуановским множеством с топологической размерностью d=0. Отсюда следуют интересные выводы. Если фотон движется по антуановской траектории, то покинуть это множество ему довольно трудно. Он испытывает проблемы с выходом в реальный мир с d=1, 2, 3, подобные затруднениям человека, находящегося в комнате без окон и дверей. Возможна и физическая интерпретация механизма удержания света в системе, обусловленная необычной топологией антуановских траекторий. Замена реального трехмерного фотона нульмерным объектом приводит к сингулярному характеру распределения энергии вдоль траектории антуановского фотона. У такой траектории появляется своеобразная “механическая жесткость”. Переплетенные “жесткие” звенья антуановского множества сопротивляются любой попытке расцепления. Это также является причиной удержания фотона вблизи пары, точнее, вблизи самого себя.

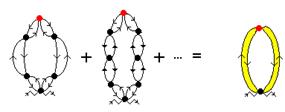Рис. 8. Антуановские кольца на траектории фотона

Рис. 9. Переплетение антуановских колец

Возможен ли выход антуановского фотона в реальный мир? Узкий пик в направлении назад при рассеянии света дисперсной системой в условиях слабой локализации и есть не что иное как испускание антуановских фотонов, инициируемое светом.

Анализ ряда теории возмущений для фотонного пропагатора в системе частиц показывает, что имеются траектории, изоморфные множеству Антуана. Эти траектории, похожие на петлю, составленную из двух частей, как кольцо наручников, представлены на Рис. 8. Два полукольца (они не обязательно одинаковые) смыкаются у верхней частицы. Сумма таких петель обозначена нами тонированным кольцом. В процессе своего движения эти кольца траектории могут переплетаться - см Рис. 9. В свою очередь, каждая пропагаторная линия, из которых состоят переплетенные кольца Рис. 9, также есть набор переплетенных колец меньшего масштаба (см. Рис. 10) Так повторяется до бесконечности.

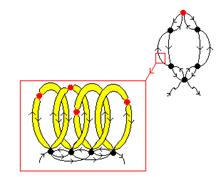Рис. 10. Структура пропагаторной линии антуановского кольца

Необходимым условием для локализации является очень сильная перенормировка или уменьшение длины волны попадающего в систему фотона. Как известно, в системах с большими значениями диэлектрической проницаемости длина волны фотона 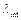становится гораздо меньше длины волны падающего фотона 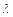. Частота фотона при этом не изменяется - изменяется эффективная скорость фотона в соответствии с соотношением . Нас интересует ситуация, при которой 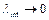, иначе фотон не «уместится» на исчезающе малых звеньях антуановского множества. Эффективная скорость фотона при этом становится нулевой.

Одним из объектов, где сильная перенормировка длины волны излучения в действительности возможна, является фрактальный кластер, состоящий из слабопоглощающих частиц-мономеров. Фрактальными называют гетерогенные системы, обладающие масштабной инвариантностью. Любой малый фрагмент системы при увеличении масштаба воспроизводит пространственную структуру всей системы. Фрактальным кластером (ФК) называют обычно агломерат микронных размеров, состоящий из нанометровых твердых частиц, удерживаемых вместе ван-дер-ваальсовскими силами. Фрактальные кластеры образуются либо в результате сильно неравновесной конденсации паров твердого вещества и последующей агрегации нанометровых частиц-мономеров, либо на начальной стадии процесса кристаллизации из растворов или расплавов.

Масштабная инвариантность кластера обусловливает сравнительно медленное спадание парных корреляций в расположении его частиц. Парная корреляционная функция устроена следующим образом

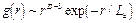
где D- фрактальная размерность кластера, 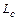- характерный размер корреляционного блока. Фрактальная размерность определяет число частиц-мономеров кластера N, находящихся внутри воображаемой сферы радиуса 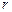: . Значение D< 3 и необязательно целое - в этом специфика фрактального кластера. В обычных плотных упаковках частиц парные корреляции спадают существенно быстрее, исчезая по экспоненциальному закону на характерных расстояниях порядка нескольких радиусов частиц. Масштабная инвариантность ФК визуально отражается в его довольно рыхлой структуре. Плотность частиц в объеме фрактального кластера не постоянна, а пропорциональна .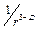

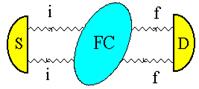Рис. 11. Удержание фотона между источником и детектором при упругом рассеянии на фрактальном кластере

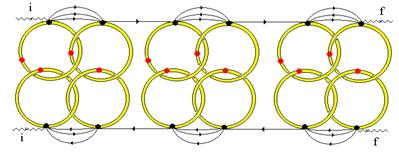Рис. 12. Физические причины удержания фотона

Причиной перенормировки являются дальнодействующие корреляции в расположении частиц ФК, визуально выражающиеся в связности кластера и наличии в нем большого числа пустот. Это объясняется следующим образом. Пусть падающий на кластер фотон с длиной волны l порядка характерного размера кластера L улавливается какой-нибудь достаточно крупной полостью ФК (резонансной полостью). Это улавливание приводит к росту эффективной диэлектрической проницаемости кластера 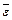( 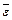растет вблизи любого электромагнитного резонанса [16]). Возрастание 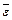инициирует, в свою очередь, уменьшение длины волны фотона, т.к. 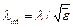. Фотон с перенормированной длиной волны 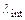находит другую полость, меньшего размера. Новое улавливание вновь стимулирует возрастание 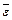и новое уменьшение 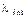и т.д. В результате все полости кластера могут оказаться заполненными перенормированными фотонами, в том числе и теми, чья длина волны .

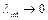Физика локализации света в фрактальных системах и схема расчета таковы. Между источником и детектором излучения постоянно присутствует фотон, «циркулирующий» по замкнутой петле (см. Рис. 11). Его удерживает там переплетение жестких антуановских колец на его траектории (см. Рис. 12). Кольца образуются в результате многократного перерассеяния фотона на частицах-мономерах фрактального кластера. В дальнейшем вычисляется амплитуда взаимодействия пары виртуальных фотонов, которые находятся внутри области, обозначенной как FC (фрактальный кластер), на рисунке 12. Один из них соответствует верхнему «берегу», второй - нижнему. Типичные процессы, формирующие эту амплитуду можно увидеть на Рис. 12, если отбросить волнистые линии реальных фотонов. Амплитуда взаимодействия ищется в виде решения соответствующего уравнения Бете-Солпитера. Можно показать, что мнимая часть этой амплитуды описывает удержание или локализацию фотона в системе.

Соответствующий расчет приводит к следующему выражению для дифференциального сечения упругого рассеяния света кластером [8]:

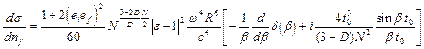(1)

где , 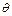- угол рассеяния, - дельта-функция Дирака, с - скорость света в вакууме, 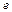- единичные векторы поляризации падающего 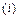и рассеянного 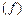квантов, - частота падающего света и 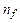- единичный вектор в направлении рассеянного фотона, 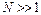- число частиц в корреляционном блоке, - диэлектрическая проницаемость материала частиц и 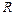- радиус частицы-мономера. Параметр 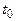от слабо зависит от 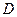. Мнимая часть сечения описывает «поглощение», обусловленное локализацией. При 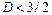это сечение очень велико.

При Q ¹ 0 дифференциальное сечение рассеяния становится чисто мнимым Это означает, что при Q ¹ 0 никакого потока рассеянного кластером света вообще не существует. Любой рассеявшийся “вбок” фотон улавливается кластером и начинает колебаться вдоль соответствующего .

Не меньшим сюрпризом выражения (1) для 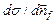является сингулярность рассеяния вперед. Имея в виду связь

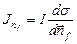
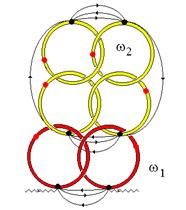Рис. 13. Физические причины вынужденного излучения света, локализованного в кластере

между потоком рассеянного в направлении излучения 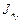и плотностью потока падающего излучения 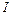, видно, что сингулярность в сечении означает, что в системе возможен конечный «ток» фотонов даже при нулевой плотности потока падающего излучения. Сингулярность 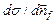в направлении вперед описывает вынужденное излучение света из кластера. Это типично «лазерный» эффект. Когерентность вынужденного излучения обеспечивается «нульмерностью» локализованных антуановских фотонов, способностью к концентрации огромного из числа в малом объеме. Физическая причина когерентного сброса этих фотонов проста и наглядна. Любой фотон, рассеявшийся «вбок» улавливается кластером и начинает осциллировать в нем вдоль направления рассеяния без права выхода из кластера. На его траектории образуются антуановские кольца, переплетенные с соответствующими кольцами локализованных фотонов. Именно это переплетение удерживает такой фотон в кластере. Больше всего таких колец у фотона, рассеивающегося на нулевой угол - мнимая часть 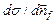имеет максимум при (см выражение (1)). И в то же время только у такого фотона есть возможность вырваться из кластера, описываемая действительной частью сечения. Этот фотон, зацепившись своими кольцами за соответствующие кольца локализованных фотонов, вытягивает их наружу (см. Рис. 13). Так на языке антуановских колец можно легко понять физику вынужденного излучения света.

Мы ожидаем, что подобного рода эффекты, а именно - локализация света, имеют место в системе скоррелированных зеркал устройства, описанного в [мы]. Здесь локализация возможна между любой парой из большого числа всевозможных комбинаций зеркал.

Считывание и запись локализованного света

Спектр собственных возбуждений любой системы в немалой степени определяется ее границей или поверхностью. Типичный пример таких возбуждений - плазмон-поляритоны на поверхности металла или поверхностные плазмоны в малых металлических частицах. Существует ли возможность «считать» характерные для такого рода возбуждений спектры и записать их на некотором носителе или накопителе информации с целью, например, длительного хранения и последующего прочтения? Мы расскажем о проблемах и перспективах этих исследований.

Как известно, при отражении фотона от плоской поверхности состояние его поляризации не меняется - это запрещено изотропностью задачи по отношению к вращениям в плоскости поверхности. Казалось бы и при отражении света от плоской пластины с двумя стенками ситуация не изменится. Однако, это не так, если мы учитываем возможность локализации света между границами пластины. Подобного рода эффекты наблюдаются при рассеянии света в направлении строго назад в однородном ансамбле мельчайших частиц [11]. Связано это с возможностью «вытаскивания» рассеянным назад фотоном фотона, локализованного в системе. В этом случае поляризация отраженного света может измениться. Причина, по которой он «вытаскивает» локализованный фотон, как мы знаем, связана не с фотон-фотонным взаимодействие, которым в данных условиях можно пренебречь, а с переплетением антуановских колец рассеивающегося и локализованного фотонов.

Этот эффект, совмещенный с вращательно-колебательными и поляризационными характеристиками изучаемых объектов, можно использовать для эффективного извлечения из объекта локализованных в нем его собственных возбуждений (его «спектра»). Рассмотрим схему, представленную на Рис. 1. В ней фигурирует лазер, описанный выше, и кристалл, чей спектр мы хотим «вытянуть» наружу. В конструкцию стандартного лазера внесено еще одно изменение. Из него удалена полупрозрачная пластинка, расположенная под углом Брюстера к оси лазера (назначение этой пластинки отсекать паразитный свет не основной поляризации). Это делается для того, чтобы не мешать свету, отраженному от кристалла и изменившему свою поляризацию в результате «вытаскивания» из кристалла локализованных фотонов, снова войти в резонатор и затем многократно повторить свой маршрут. Мы ожидаем, что эффективность «вытаскивания» локализованных фотонов, записавших информацию об объекте, в такой системе окажется достаточно высокой для его экспериментального наблюдения. Далее эти делокализованные фотоны могут снова локализоваться но уже в системе зеркал лазера. После этого мы убираем кристалл, но «спектр» его возбуждений, локализованный в лазере, как мы ожидаем, будет еще какое-то время себя проявлять. Система будет воспроизводить спектральную память об объекте, который уже выведен из области экспонирования. Роль кристалла может выполнять любая система, в которой возможна локализация поля. Например, это могут быть биологические объекты, в частности, генетические структуры, которые имеют фрактальную жидкокристаллическую упаковку. Вероятно, именно такого рода эффекты спектральной памяти наблюдались в наших экспериментах (см. выше).

Подчеркнем, что речь идет о возможности считывания лазерным излучением с фиксированной частотой 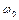именно всего спектра объекта - в широком частотном диапазоне. Дело в том, что лазерному фотону с частотой 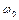«безразлично» какой локализованный фотон «вытаскивать» из объекта: с той же самой частотой 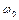или с любой другой, если она имеется.