
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Локализованный свет и проблемы квантовой телепортации
|
|
Совершенно неожиданное приложение идеи локализации света находят в проблеме квантовой телепортации - мгновенной передаче послания на произвольно большие расстояния. Эта экзотическая область исследований, начиная с работ [2, 3], привлекает все большее внимание физиков, а в последнее время и биологов. Коротко напомним основные положения «классической» теории квантовой телепортации.
Как известно, любая волновая функция пары фотонов (фотон 2 и фотон 3), каждый из которых обладает двумя состояниями поляризации (горизонтальной поляризацией 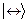 и вертикальной поляризацией
и вертикальной поляризацией  ), можно разложить по четырем базисным состояниям (по так называемым состояниям Белла), которые образуют полную ортонормированную систему функций [22]
), можно разложить по четырем базисным состояниям (по так называемым состояниям Белла), которые образуют полную ортонормированную систему функций [22]
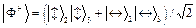
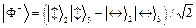

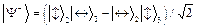 (2)
(2)
Состояние 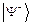 (в дальнейшем оно нас будет интересовать больше, чем остальные) обладает интересным свойством: при обнаружении одного из фотонов с определенной поляризацией поляризация другого оказывается противоположной.
(в дальнейшем оно нас будет интересовать больше, чем остальные) обладает интересным свойством: при обнаружении одного из фотонов с определенной поляризацией поляризация другого оказывается противоположной.
Возможность экспериментально отличить одно из белловских состояний от других обеспечивается их различными симметриями. Из четырех состояний (2) первые три являются бозонными состояниями (их волновая функция не меняет знак при перестановке частиц 2 и 3). Последнее состояние 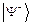 - фермионное (при перестановке 2 и 3 знак волновой функции изменяется). Эта особенность состояния
- фермионное (при перестановке 2 и 3 знак волновой функции изменяется). Эта особенность состояния 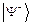 позволяет выделить его в ряде хорошо описанных в литературе экспериментов, использующих интерференцию двух специальным образом приготовленных световых пучков [3].
позволяет выделить его в ряде хорошо описанных в литературе экспериментов, использующих интерференцию двух специальным образом приготовленных световых пучков [3].
Имея в виду возможность работать далее с состоянием 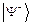 , в дальнейшем используется ставшая уже классической следующая экспериментальная схема [2, 3, 22]. Есть два участника игры - Алиса и Боб, и источник пары фотонов, описываемых состоянием
, в дальнейшем используется ставшая уже классической следующая экспериментальная схема [2, 3, 22]. Есть два участника игры - Алиса и Боб, и источник пары фотонов, описываемых состоянием 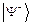 . Задача Алисы - передать имеющийся у нее фотон 1 Бобу, находящемуся как угодно далеко от нее. Однако, Алиса не пользуется обычным классическим способом, а поступает следующим образом. Алиса и Боб одновременно получают пару фотонов 2 и 3, описываемую состоянием
. Задача Алисы - передать имеющийся у нее фотон 1 Бобу, находящемуся как угодно далеко от нее. Однако, Алиса не пользуется обычным классическим способом, а поступает следующим образом. Алиса и Боб одновременно получают пару фотонов 2 и 3, описываемую состоянием 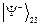 . Алиса получает фотон 2, а Боб - фотон 3. Алиса «смешивает» фотон 1 и 2. При этом в одном случае из четырех она имеет возможность наблюдать состояние
. Алиса получает фотон 2, а Боб - фотон 3. Алиса «смешивает» фотон 1 и 2. При этом в одном случае из четырех она имеет возможность наблюдать состояние
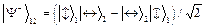
Как только она это обнаружит, немедленно фотон 3 переходит в начальное состояние фотона 1. Причина этого следующая. Наблюдение Алисой состояния 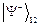 означает, что при каком-то состоянии фотона 1 фотон 2 будет в противоположном по поляризации состоянии. Но поскольку фотоны 2 и 3 находятся также в состоянии
означает, что при каком-то состоянии фотона 1 фотон 2 будет в противоположном по поляризации состоянии. Но поскольку фотоны 2 и 3 находятся также в состоянии 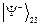 , фотон 3 будет в состоянии, ортогональном состоянию 2, т.е. в состоянии фотона 1. Таким образом, происходит телепортация фотона 1 от Алисы к Бобу, независимо от расстояния между ними. Телепортация осуществляется мгновенно.
, фотон 3 будет в состоянии, ортогональном состоянию 2, т.е. в состоянии фотона 1. Таким образом, происходит телепортация фотона 1 от Алисы к Бобу, независимо от расстояния между ними. Телепортация осуществляется мгновенно.
Правда, при такой телепортации поляризационное состояние телепортируемого фотона 1 Алисе неизвестно, т.к. фотон 1 смешивается с фотоном 2, образуя состояние 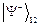 .
.
Описанная процедура телепортации безупречна с точки зрения формализма квантовой механики. Тем не менее, физический смысл базисных состояний Белла остается неясным, так же как и нет полной ясности в разрешении парадокса Эйнштейна-Подольского-Розена (ЭПР-парадокс) [4], для описания которого эти состояния, собственно, и были введены. Как понять, что при измерении поляризации 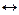 одного из фотонов, находящихся, например, в состоянии
одного из фотонов, находящихся, например, в состоянии 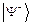 , поляризация другого мгновенно оказывается
, поляризация другого мгновенно оказывается 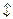 , несмотря на то, что их разделяет очень большое расстояние и любая информация относительно состояния второго сможет поступить к нам спустя вполне определенный промежуток времени.
, несмотря на то, что их разделяет очень большое расстояние и любая информация относительно состояния второго сможет поступить к нам спустя вполне определенный промежуток времени.
Пары фотонов, описываемые состояниями (2) или их линейными комбинациями, называют обычно ЭПР-фотонами или перепутанными фотонами. До тех пор, пока мы не поймем физическую причину мгновенных корреляций в свойствах этих фотонов, мы не поймем физику телепортации, несмотря на всю безупречность логических построений.
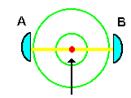 Рис. 14. Схема эксперимента по считыванию, записи и хранению информации
Рис. 14. Схема эксперимента по считыванию, записи и хранению информации
|
Как это не удивительно, но к проблемам ЭПР-парадокса и телепортации можно подойти и с другой стороны - с позиций существования локализованного света. Один из вариантов ЭПР-парадокса следующий. Рассматривается, к примеру, s-рассеяние фотона сферической частицей, т.е. рассеянная волна сферически изотропна (см. Рис. 14). Пусть рассеянный фотон подходит к детектору в точке А (Алиса). Этот акт регистрации позволяет нам сделать вывод, что в тот же самый момент времени этот рассеянный фотон достигает детектора, расположенного, к примеру, в точке В (Боб), отстоящей от А на сколь-угодно большое расстояние. Это при том, что любая информация из В в А может быть передана по истечении только вполне определенного промежутка времени. Если не рассматривать возможность сверхсветовой скорости распространения сигналов, понять ситуацию можно следующим образом. Что если регистрируемый акт прихода света в А связан вовсе не с рассеянным фотоном, а со сбитым из “трубки” АВ локализованным «длинным» фотоном? Мы “ловим” его левый “конец”. Тогда в том, что в тот же самый момент времени происходит «регистрация» в точке В его “правого” конца, нет ничего странного. Никакого сверхсветового распространения сигнала не происходит, как не происходит и распространения сигнала вообще. «Длинный» локализованный фотон вытаскивается из «полости» за счет зацепления жестких антуановских колец локализованного и рассеивающегося фотонов. Это зацепление аналогично рассмотренному выше зацеплению в фрактальном кластере.
Предположим теперь, что никакого фотона, рассеивающегося на частице нет. А есть «полость» между Алисой и Бобом, заполненная локализованным в ней фотоном. Алиса посылает в эту полость свой фотон. Этот фотон зацепляет по известному нам механизму локализованный фотон и предоставляет его Бобу. Таким образом, в результате действий Алисы, Боб немедленно получает некоторую информацию, правда неизвестно какую, поскольку многие свойства локализованного фотона никому неизвестны.
Как мы видим, в данном случае для мгновенной «передачи» сигнала вместо пары ЭПР-коррелированных фотонов достаточно иметь дело с одним-единственным локализованным фотоном (впрочем, при желании его можно рассматривать как пару взаимодействующих между собой виртуальных фотонов - фотон верхнего берега и фотон нижнего берега рисунков 1 и 2). Кроме того, в [3] ЭПР-пара телепортировала Бобу неизвестный фотон Алисы. В нашем случае фотон Алисы, воздействовав на левый конец никому неизвестного локализованного фотона, предоставляет его правый конец Бобу. В этом вся разница и сходство двух механизмов телепортации.
Противоречит ли телепортация основам специальной теории относительности, утверждающей, что скорость передачи информации не может превосходить скорость света? Очевидно, нет. В случае телепортации беннетовского типа [2, 3] мгновенно передается никому неизвестный сигнал. В рамках нашей модели вообще ничего не передается. Боб получает то, что уже находится рядом с ним, но до поры-до времени ему недоступно. Информация уже предсуществует. Алиса мгновенно «разрешает» Бобу взять ее. Поэтому такую модификацию квантовой телепортации (нелокальности) мы назвали пермиссивной (от английского “permission” – разрешение). Надо отметить также, что такая нелокальнсть распространяется, видимо, и дальше, поскольку в нашем случае фотоны, промодулированные объектом, мгновенно (нелокально) превращаются в радиоволны, хранящие «фотонную поляризационную информацию». Возможно также, что в наших экспериментах зондирующие объект и интерферирующие встречные фотоны записывают динамичную поляризационную голограмму объекта, например ДНК, и превращают ее в биоактивную радиоволновую, изоморфную фотонной, голограмму.
Генерация радиоволн при неупругом рассеянии света
В этом разделе мы качественно обсудим одну из возможных причин генерации радиоволн ПЛР-спектрометром. Речь пойдет о новом механизме неупругого рассеяния света в электронных системах - в данном случае, в системе металлических слоев зеркальных покрытий резонатора лазера, являющегося основным элементом спектрометра. Этот механизм отличается от традиционного комбинационного рассеяния фотонов. В отличие от дискретного набора стоксовских и антистоксовских пиков спектр рассматриваемого неупруго рассеянного света является непрерывным и занимает весь диапазон частот от 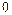 до
до 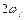 , где
, где  - частота падающего фотона.
- частота падающего фотона.
Физика рассматриваемого неупругого рассеяния очень проста. Мы установим основные его закономерности на примере неупругого рассеяния с возбуждением объемных и поверхностных плазмонов в малой металлической частице. Поверхностными плазмонами называют собственные электромагнитные моды мельчайших металлических частиц [16]. Они связаны с собственными колебаниями взаимодействующих через кулоновский потенциал электронов проводимости частицы. Эти моды проявляют себя как отчетливые резонансы в спектрах упругого рассеяния и поглощения света малыми металлическими частицами. Частоты поверхностных плазмонов в зависимости от концентрации электронов проводимости внутри частиц принадлежат границе видимого-УФ света и определяются следующей формулой
 ,
,
где 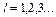 , а w0 - классическая плазменная частота неограниченного электронного газа
, а w0 - классическая плазменная частота неограниченного электронного газа
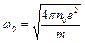 ,
,
где n0 - плотность электронов проводимости в металле, e и m - заряд и масса электрона. Возбуждение с  называют дипольным поверхностным плазмоном, а возбуждение с частотой
называют дипольным поверхностным плазмоном, а возбуждение с частотой 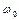 - объемным плазмоном. Подобного рода колебания существуют и в тонких металлических пленках, которыми обычно моделируют зеркальные покрытия, типа тех, что используются в рассматриваемом лазере. Здесь их называют плазмон-поляритонными модами, их свойства иные, но на данном этапе мы интересуемся лишь физикой явления.
- объемным плазмоном. Подобного рода колебания существуют и в тонких металлических пленках, которыми обычно моделируют зеркальные покрытия, типа тех, что используются в рассматриваемом лазере. Здесь их называют плазмон-поляритонными модами, их свойства иные, но на данном этапе мы интересуемся лишь физикой явления.
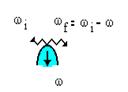 Рис. 15. Классическая схема неупругого рассеяния фотонов
Рис. 15. Классическая схема неупругого рассеяния фотонов
|
Классический механизм неупругого рассеяния света частицей заключается в следующем. Подлетающий к частице фотон с энергией 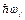 возбуждает в ней флуктуацию электронной плотности, сбрасывая на это часть своей энергии
возбуждает в ней флуктуацию электронной плотности, сбрасывая на это часть своей энергии 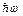 . Энергия вылетающего фотона
. Энергия вылетающего фотона 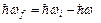 . Этот процесс символически изображен на Рис. 15. Заштрихованный уголок - флуктуация электронной плотности
. Этот процесс символически изображен на Рис. 15. Заштрихованный уголок - флуктуация электронной плотности 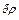 , которая есть суперпозиция большого числа электронно-дырочных пар, возбуждаемых фотоном. Сечение процесса особенно велико, если фотону удается «раскачать» дипольный поверхностный и объемный плазмоны. Для частицы, чей размер много меньше длины волны подлетающего фотона, дифференциальное сечение неупругого рассеяния следующее [7]
, которая есть суперпозиция большого числа электронно-дырочных пар, возбуждаемых фотоном. Сечение процесса особенно велико, если фотону удается «раскачать» дипольный поверхностный и объемный плазмоны. Для частицы, чей размер много меньше длины волны подлетающего фотона, дифференциальное сечение неупругого рассеяния следующее [7]
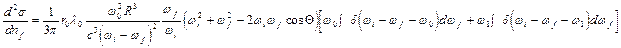 (1),
(1),
где 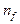 - единичный вектор в направлении рассеянного кванта,
- единичный вектор в направлении рассеянного кванта, 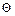 - угол рассеяния, R - радиус отдельной частицы пары,
- угол рассеяния, R - радиус отдельной частицы пары,  и
и 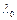 - классический радиус электрона и комптоновская длина волны электрона соответственно,
- классический радиус электрона и комптоновская длина волны электрона соответственно,
Если энергии, сброшенной фотоном, хватит на возбуждение плазмонов 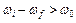 , то
, то
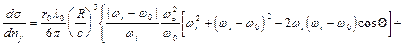
 (2)
(2)
Как мы видим из анализа выражения (1), возможен только дискретный сброс энергии фотона, соответствующий возбуждению объемного и дипольного поверхностного плазмона. Это отражено присутствием дельта-функций Дирака в соответствующем выражении. Сечение процесса меньше сечения упругого рассеяния света частицей в  раз.
раз.
 Рис. 16. Предлагаемый механизм неупругого рассеяния фотонов
Рис. 16. Предлагаемый механизм неупругого рассеяния фотонов
|
Предлагаемый нами механизм принципиально иной. Предположим, что между источником излучения и детектором непрерывно «циркулирует» по замкнутой петле фотон, многократно обмениваясь сам с собой флуктуациями электронной плотности, возбуждаемыми в некоторой системе рассеивателей, находящейся между источником и детектором. Этот процесс изображен на Рис.16. Заштрихованные петли описывают распространение флуктуации электронной плотности в системе рассеивателей - это так называемые приводимые поляризационные операторы плотность-плотность или просто корреляторы электронной плотности [24]. Волнистые линии - волновые функции реальных фотонов, горизонтальные линии - фотонные пропагаторы. Например, верхняя вершина произвольной нечетной петли описывает рождение флуктуации электронной плотности фотоном с энергией  за счет уменьшения его энергии на
за счет уменьшения его энергии на  , а нижняя - ее схлопывание за счет получения фотоном энергии
, а нижняя - ее схлопывание за счет получения фотоном энергии  обратно. Таких петель на траектории фотона может быть сколько угодно. Наш фотон бесконечное число раз обменивается энергией сам с собой в процессе неупругого рассеяния. В результате возникает своеобразное обменное взаимодействие фотона с самим собой, аналогичное обычному обменному взаимодействию квантовой химии. Именно это взаимодействие удерживает фотон в «полости» между источником и детектором, обосновывая наше предположение о возможности столь странной, на первый взгляд, «циркуляции» фотона между источником и детектором.
обратно. Таких петель на траектории фотона может быть сколько угодно. Наш фотон бесконечное число раз обменивается энергией сам с собой в процессе неупругого рассеяния. В результате возникает своеобразное обменное взаимодействие фотона с самим собой, аналогичное обычному обменному взаимодействию квантовой химии. Именно это взаимодействие удерживает фотон в «полости» между источником и детектором, обосновывая наше предположение о возможности столь странной, на первый взгляд, «циркуляции» фотона между источником и детектором.
Дифференциальное сечение рассматриваемого процесса имеет вид
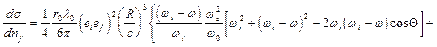

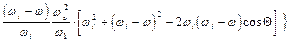 (3)
(3)
где 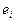 и
и 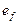 -единичные вектора поляризации и
-единичные вектора поляризации и  - сброшенная частота.
- сброшенная частота.
Между выражениями (2) и (3), несмотря на их внешнее сходство, имеется принципиальная разница. В рамках классического механизма возможен только дискретный сброс энергии падающего фотона, соответствующий возбуждению объемного (с частотой 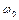 ) и дипольного поверхностного плазмонов (частота
) и дипольного поверхностного плазмонов (частота 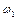 ) в частицах (любой другой сброс энергии запрещен фигурирующими в (1)
) в частицах (любой другой сброс энергии запрещен фигурирующими в (1) 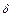 -функциями). Что касается предлагаемого механизма, то красный сдвиг частоты падающего фотона может быть любым в интервале от 0 до
-функциями). Что касается предлагаемого механизма, то красный сдвиг частоты падающего фотона может быть любым в интервале от 0 до 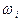 . Если
. Если  , результатом процесса является наблюдаемая экспериментально генерация радиоволн.
, результатом процесса является наблюдаемая экспериментально генерация радиоволн.
Наряду с «красным» смещением возможен и «голубой» сдвиг частоты фотона.. Таким образом, спектр неупруго рассеянного света с учетом локализации должен занимать весь диапазон частот от 0 до 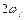 . Подобного рода эффекты действительно наблюдаются в экспериментах по гигантскому комбинационному рассеянию света молекулами, адсорбированными на поверхности мельчайших металлических частиц - его называют «гигантский белый фон», и он до сих пор остается загадкой [27].
. Подобного рода эффекты действительно наблюдаются в экспериментах по гигантскому комбинационному рассеянию света молекулами, адсорбированными на поверхности мельчайших металлических частиц - его называют «гигантский белый фон», и он до сих пор остается загадкой [27].
Процессы Рис. 16 при  качественно объясняют повышенный фон радиоизлучения рассматриваемого лазера. Количественный расчет безусловно требует учета специфики системы.
качественно объясняют повышенный фон радиоизлучения рассматриваемого лазера. Количественный расчет безусловно требует учета специфики системы.
ЛИТЕРАТУРА
1. Albada P. van, Lagendijk A., Observation of Weak Localization of Light in a Random Medium, Phys. Rev. Lett. 55, 1985, p. 2692-2695.
2. Bennet C.H., Brassard G., Crepeau C., Jossa R., Peres A., Wootters W.K., Teleporting and unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys.Rev.Lett., v.70, p.1895-1899 (1993).
3. Bouwmeester D., Pan Jian-Wei, Mattle K., Eibl M., Weinfurter H., Zeilinger A., Experimental quantum teleportation. Nature, v.390, p.575-579 (1997).
4. Einstein A., Podolsky B., Rosen N., Can quantum-mechanical description of physical reality be considered complete? // Phys.Rev. 1935, v.47, p.777-780.
5. Gariaev P., Tertishny G., 1999. The quantum nonlocality of genomes as a main factor of the biomorphogenesis. Inern. Conf. Potsdam. Germany.
6. Lagendijk A., van Tiggelen B.A., Resonant Multiple Scattering of Light, Physics Reports, v. 270, p. 143-216, 1996.
7. Lushnikov A.A., Maksimenko V.V.,.Simonov A.J, Electromagnetic Surface Modes in Small Metallic Particles, in Electromagnetic Surface Modes, ed. by A.D.Boardman, J. Wiley, Chichester, 1982, pp. 305-345.
8. Maksimenko V.V., Antoine’s Localization of Photon inside Fractal Cluster, Fractal in Engineering, Delft, Netherlands, 1999, p. 355-358.
9. Maksimenko V.V., Localization of Light in Fractal Cluster, J. of Aerosol Science, v. 30, 1999, p. 287-288.
10. Maksimenko V.V., Localization of Photon between Pair of Particles-2. Inelastic Scattering, J. of Aerosol Science, v. 30, 1999, p. 289-290.
morphogenesis of biosystems. // 3th Scientific and medical network continental members meeting. Potsdam, Germany. May 6-9, 1999, p.37-39.
11. Mаксименко B.B.,. Крикунов В.А,. Лушников А.А, Сильная локализация света в плотноупакованных гранулированных средах, ЖЭТФ, т. 102, 1992, c.1571.
12. Sheng P. (Ed.), Scattering and Localization of Classical Waves in Random Media. World Scientific. Signapore, 1990.
13. Sheng P., Introduction to Wave Scattering, Localization, and Mesoscopic Phenomena. Academic, San Diego, 1995.
14. Абрикосов A.A., Основы теории металлов. Наука. Москва, 1987, с.183.
15. Болтянский В.Г., Ефремович В.А, Наглядная топология, Москва, Наука, 1982, с. 84.
16. Борен К., Хафмен Д., Поглощение и рассеяние света малыми частицами. Москва, Мир, 1986, с. 77.
17. Гаряев П.П. Волновой генетический код. М. 1997. Издатцентр. 108с.
18. Гаряев П.П. Волновой геном. М. Общественная польза. 1994. 279с.
19. Гаряев П.П., Гарбер М.Р., Леонова Е.А., Тертышный Г.Г. К вопросу о центральной догме молекулярной биологии. Сознание и физическая реальность. 1999, Изд. ФОЛИУМ. Т.4, №1, с.34-46.
20. Гаряев П.П., Тертышный Г.Г. Явление перехода света в радиоволны применительно к биосистемам. Сборник научных трудов. Академия медико-технических наук РФ. Отделение «Биотехнические системы и образование» при МГТУ им. Н.Э.Баумана. 1997, Выпуск 2. с. 31-42.
21. Гаряев П.П., Тертышный Г.Г., Готовский Ю.В. Трансформация света в радиоволны. III международная конференция «Теоретические и клинические аспекты применения адаптивной резонансной и мультирезонансной терапии». «ИМЕДИС». Москва. 18-20 апреля 1997г. с.303-313.
22. Кадомцев Б.Б., Динамика и информация, Москва, Редакция журнала “Успехи физических наук”, 1999, 400 с.
23. Ландау Л.Д., Лифшиц Е.М., Квантовая механика, Москва, Наука, 1974, 752 с.
24. Лушников А.А., Максименко В.В., Квантовая оптика металлической частицы, ЖЭТФ, т.103, 1993, с.1010- 1044.
25. Мулдашев Э.Р., Комбинированная трансплантация глаза. Министерство здравоохранения Российской Федерации, Всероссийский Центр Глазной и Пластической Хирургии. «Аллоплант», 2000.
26. Прангишвили И.В., Гаряев П.П., Тертышный Г.Г., Леонова Е.А., Мологин А.В., Гарбер М.Р., Генетические структуры как источник и приемник голографической информации, Датчики и Системы, №2, 2000, с.2-8.
27. Ченг Р. и Фуртак Т. (редакторы)Гигантское комбинационное рассеяние. Москва. Мир, 1984, 408 с.
СПЕКТРОСКОПИЯ РАДИОВОЛНОВЫХ ИЗЛУЧЕНИЙ ЛОКАЛИЗОВАННЫХ ФОТОНОВ: ВЫХОД НА КВАНТОВО-НЕЛОКАЛЬНЫЕ БИОИНФОРМАЦИОННЫЕ ПРОЦЕССЫ